【C++天梯计划】1.6 深搜(DFS deep search)

今天我要开启一个新计划----【C++天梯计划】
目的是通过天梯计划，通过题目和知识点串联的方式，完成C++复习与巩固。

什么是深搜？

所谓深搜（也叫回溯法）就是采用的是“一直往下走，走不通了就掉头，换一条路再往下走”总结来说就是递归的枚举深度优先搜索的实质就是穷举，按照一定的顺序和规则不断地去尝试，直到找到问题的解。对于一个问题的第一个状态叫做初始状态，最后要求的状态叫做目的状态。在搜索的过程中，对当前状态进行检测，如果当前状态满足目的状态，那么这个当前状态就是结果之一。

模拟深搜

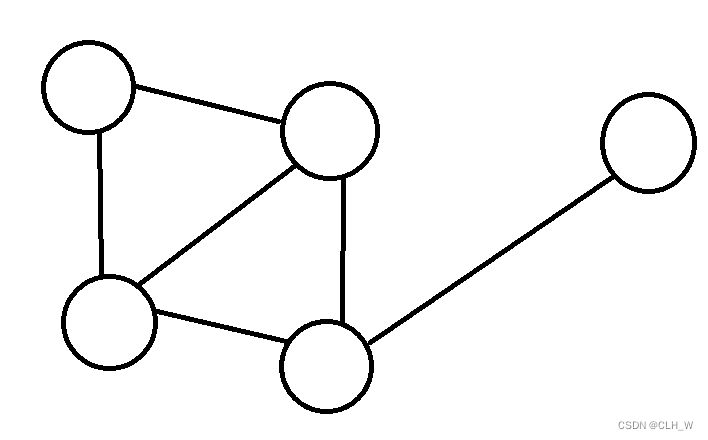
选择A作为源节点------>（继续下一层深搜）访问到了B------->（继续下一层深搜）访问到了D------>（继续下一次深搜）搜索到了C------>(此时发现C的所有下一节点都已经被访问过了）返回C的上以节点D（因为是从D访问到C来的，所以不要走回到C的其他上节点）------>我们再遍历D的其他子节点E------->（发现E没有子节点）返回上一节点D------>（发现D没有未被访问的子节点）返回B------>(B没有被访问的子节点）返回A------>（A没有未被访问的子节点）DFS完毕，因此，此图的深搜遍历顺序：A—>B—>D—>C—>E

总结深搜的思路： 沿着某条路径遍历，直到末端，然后回溯，再遍历另一条路径（走没有走过的岔路口）做同样的遍历，直到所有的节点都被访问，即回溯到源节点并且源节点已无未被访问的子节点。

例题1：卒的遍历

题目描述

在一张 n \times mn×m 的棋盘上（如 66 行 77 列）的最左上角 (1,1)(1,1) 的位置有一个卒。该卒只能向下或者向右走，且卒采取的策略是先向下，下边走到头就向右，请问从 (1,1)(1,1) 点走到 (n,m)(n,m) 点可以怎样走，输出这些走法。

输入

两个整数 n，mn，m 代表棋盘大小（3≤n≤8,3≤m≤83≤n≤8,3≤m≤8）

输出

卒的行走路线。

输入输出样例

输入
3 3
输出
1:1,1->2,1->3,1->3,2->3,3
2:1,1->2,1->2,2->3,2->3,3
3:1,1->2,1->2,2->2,3->3,3
4:1,1->1,2->2,2->3,2->3,3
5:1,1->1,2->2,2->2,3->3,3
6:1,1->1,2->1,3->2,3->3,3

代码：

#include 
using namespace std;
//只能向下或者向右走：优先向下，其次向右 
int n,m;
int r[20][3];//存储行走路径 
//方向的变化 
int fx[3] = {0,1,0};
int fy[3] = {0,0,1}; 
int c;//计数器 

void print(int k){
	c++;
	cout<<c<<":";
	//除了最后一个点以外 
	for(int i = 1;i < k;i++){
		cout<<r[i][1]<<","<<r[i][2]<<"->";
	}
	cout<<n<<","<<m<<endl;
} 

//向r数组下标为k的那一行，记录x,y点 
void dfs(int x,int y,int k){
	//记录坐标 
	r[k][1] = x;
	r[k][2] = y;
	
	//如果走到了终点，打印路径
	if(x == n && y == m){
		print(k);
		//停止递归函数，到了终点打印，就不需要继续递归了
		return; 
	} 
	
	int tx,ty;
	for(int i = 1;i <= 2;i++){
		tx = x + fx[i];
		ty = y + fy[i];
		
		//判断tx,ty有效
		if(tx>=1&&tx<=n&&ty>=1&&ty<=m){
			dfs(tx,ty,k+1);
		} 
	}
} 

int main(){
	cin>>n>>m; 
	//向r数组下标为1的那一行，记录1,1点 
	dfs(1,1,1);
}

例题2：走出迷宫的最少步数

题目描述

一个迷宫由 RR 行 CC 列格子组成，有的格子里有障碍物，不能走；有的格子是空地，可走。
给定一个迷宫，求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走，不能斜着走。

输入

第一行是两个整数，RR 和 CC ，代表迷宫的行数和列数。（ 1 ≤ R,C ≤ 401≤R,C≤40 )
接下来是 RR 行，每行 CC 个字符，代表整个迷宫。空地格子用’.‘表示，有障碍物的格子用’#‘表示。
迷宫左上角和右下角都是’.'。

输出

输出从左上角走到右下角至少要经过多少步（即至少要经过多少个空地格子）。
计算步数要包括起点和终点。

输入输出样例

输入
5 5
…###
#…
#.#.#
#.#.#
#.#…
输出
9

思路

1、准备一个整数数组，记录从出发点到每个点至少需要多少步，初始化为INT_MAX；
2、从出发点开始探测，顺时针探测，如果该点可达，且到该点的步数更少，则替换d数组的步数；
3、最终d数组记录了到每个点至少需要多少步，d[n][m]就是最终结果；

代码：

#include 
using namespace std;
int n,m;
char a[50][50];//地图 
int d[50][50];//存储走到每个点最少需要多少步 
//方向值变化的数组 
int fx[5] = {0,0,1,0,-1};
int fy[5] = {0,1,0,-1,0};

//递归探索地图，求到走到每个点最少需要多少步 
void dfs(int x,int y,int dep){
	d[x][y] = dep;
	
	int tx,ty;
	//循环数组，得到4个新的方向，递归探索4个方向 
	for(int i = 1;i <= 4;i++){
		tx = x + fx[i];
		ty = y + fy[i];
		
		//如果tx,ty可以探索（该点在地图内，且该点是.，且走到该点的步数更少）
		if(a[tx][ty]=='.'&&dep+1<d[tx][ty]){
			dfs(tx,ty,dep+1); 
		} 
	}
}

int main(){
	int i,j;
	cin>>n>>m;
	for(i = 1;i <= n;i++){
		for(j = 1;j <= m;j++){
			cin>>a[i][j];
			//将最少步数初始值设为INT_MAX
			d[i][j] = INT_MAX; 
		}
	}
	
	//调用函数
	dfs(1,1,1); 
	
	cout<<d[n][m];
	
}