04 单链表
目录
- 链表的概念和结构
- 单链表
- OJ练习
1. 链表的概念和结构
1.1 链表的概念
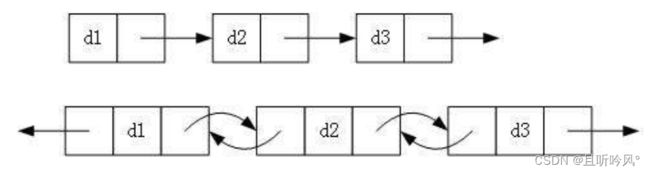
链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的
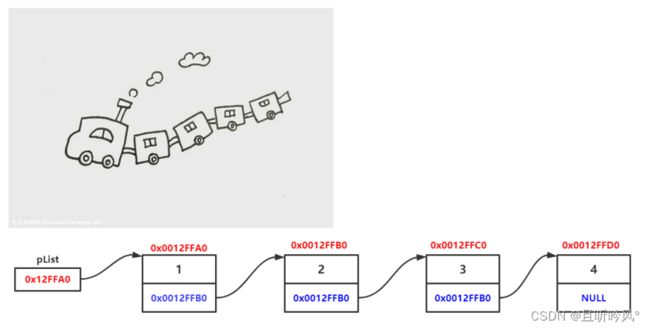1.从上图可以看出链式结构在逻辑上是连续的，物理上不一定连续
2.现实中的节点一般都是从堆上申请出来的
3.从堆上申请的空间，是按照一定的策略来分配的，两次申请的空间可能连续，也可能不连续
1.2 链表的分类
以下情况组合起来可能有8种链表结构
1.单向或者双向
2.带头或者不带头
3.循环或非循环
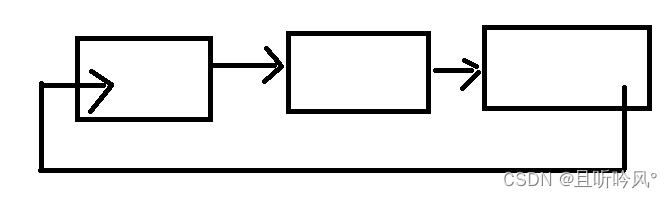
虽然有这么多链表结构，但我们常用的还是两种结构
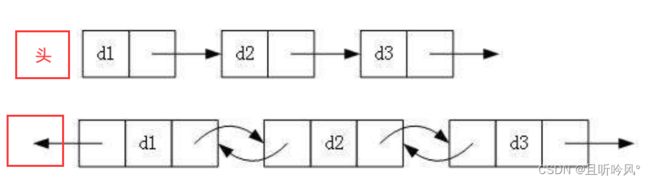
无头单向非循环链表
带头双向循环
1.无头单向非循环链表：结构简单，一般一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现更多
2.带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现
2. 单链表
头文件
#pragma once
//数据类型
typedef int DataType;
//结构
typedef struct _SListNode
{
DataType data;
struct _SListNode* pNext;
}SListNode;
//插入
void PushFront(SListNode** pHead, DataType data);
void PushBack(SListNode** pHead, DataType data);
//pos之前插入
void Insert(SListNode** pHead, SListNode* pPos, DataType data);
//pos之后插入
void InsertAfter(SListNode** pHead, SListNode* pPos, DataType data);
//查找
SListNode* Find(SListNode* pHead, DataType data);
//删除
void PopFront(SListNode** pHead);
void PopBack(SListNode** pHead);
void Erase(SListNode** pHead, SListNode* pos);
// 删除pos位置后面的值
void EraseAfter(SListNode* pos);
//打印
void PrintList(SListNode* pHead);
//销毁
void Destory(SListNode** pHead);
实现文件
#include "SList.h"
#include 主文件
#define _CRT_SECURE_NO_WARNINGS 1
#include 单链表的实现中需要注意的问题，一个是如果需要改变链表的指针位置，则需要传入二级指针。不用二级指针则需要返回新的头。assert需要断言的地方有哪些，如果操作会崩溃的地方必须断言，断言是一种严厉的检查，if判断则是温柔的检查。
在插入和删除等这些操作的时候，需要考虑只有一个节点的情况，如果传入节点可以为空，也要考虑为空的情况，pos位置的合理性也需要断言或考虑在内
在插入的时候也有一种取巧的办法，将新节点和前一个节点的值直接替换，这样在之前插入只需要遍历一次
3. OJ练习
3.1 移除元素
移除链表元素:https://leetcode.cn/problems/remove-linked-list-elements/description/
解析
这个考虑的是链表的删除操作，需要一前一后两个指针才能删除当前节点。同时，不要忘了考虑只有一个节点，头删的情况
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val) {
struct ListNode* pPrev = NULL;
struct ListNode* pCur = head;
while (pCur != NULL)
{
if (pCur->val == val)
{
//判断是不是第一个节点
if (pCur == head)
{
//头删
pCur = pCur->next;
free(head);
head = pCur;
}
else
{
//不是头删,移除元素
pPrev->next = pCur->next;
free(pCur);
pCur = pPrev->next;
}
}
else
{
pPrev = pCur;
pCur = pCur->next;
}
}
return head;
}
另一种思路，可以将不是6的元素放入新链表尾插，然后返回新的链表头。需要考虑第一个节点的情况和每次插入后下节点置空
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val) {
struct ListNode* pCur = head;
struct ListNode* NeoHead = NULL;
struct ListNode* tail = NULL;
while (pCur != NULL) {
//不是该值的放入新链表
if (pCur->val != val) {
if (tail == NULL) {
NeoHead = pCur;
} else {
tail->next = pCur;
}
tail = pCur;
pCur = pCur->next;
}
//是该值释放
else {
struct ListNode* del = pCur;
pCur = pCur->next;
free(del);
}
//第一个节点或空链表tail不能置空
if (tail != NULL) {
//最后一个节点断掉
tail->next = NULL;
}
}
return NeoHead;
}
3.2 反转单链表
反转链表: https://leetcode.cn/problems/reverse-linked-list/description/
解析
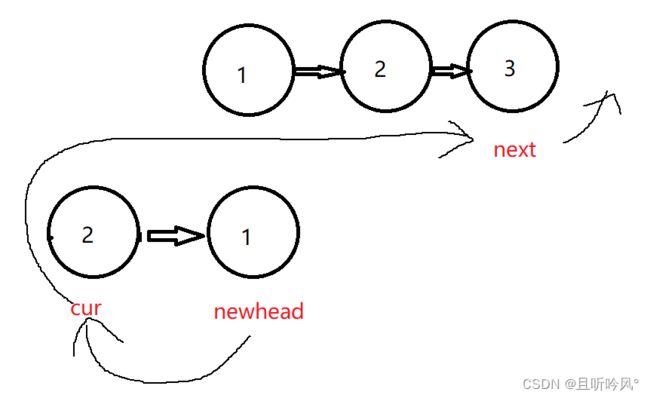
两种思路大体差不多,第一种是将每个节点的指向反过来，第二种是每拿到一个节点直接头插。这里演示第二种思路，可以少一些判断
需要三个变量，cur和newhead用来头插交换指向，newhead记录新的头节点，next记录下一个用来插入的元素
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* reverseList(struct ListNode* head) {
struct ListNode* newhead = NULL;
struct ListNode* cur = head;
while(cur != NULL)
{
//记录下一个插入的元素
struct ListNode* next = cur->next;
//头插
cur->next = newhead;
//移动头节点
newhead = cur;
//迭代
cur = next;
}
return newhead;
}
3.3 中间节点
链表中间节点https://leetcode.cn/problems/middle-of-the-linked-list/
第一种思路:
遍历求出链表长度返回需要的中间节点的链表
第二种思路：
慢指针每次走一步，快指针每次走两步，当快指针走完的时候，慢指针刚好走了链表一半，画图来分开链表奇数个和偶数个的情况
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* middleNode(struct ListNode* head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
while(fast != NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
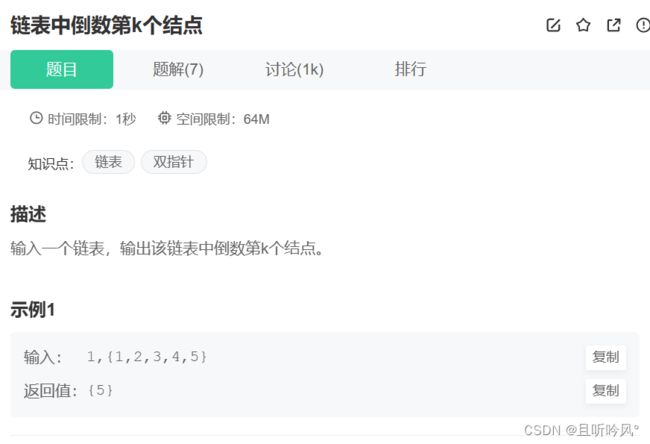
3.4 倒数第k节点
链表倒数第k个节点：https://www.nowcoder.com/practice/529d3ae5a407492994ad2a246518148a?tpId=13&&tqId=11167&rp=2&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
第一个方法: 求链表总长度，减去k就知道返回哪个节点的值
第二个方法：和上面思路一样，用一个快慢指针，让两个指针拉开差距，返回第k个节点就让快指针走几步，然后同时移动两个指针，直到快指针为空返回慢指针的值
其中有两点需要判断，如果传入的是空指针返回空，如果快指针在拉开距离的时候是空，说明要返回的值超出链表范围，也返回空
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
/**
*
* @param pListHead ListNode类
* @param k int整型
* @return ListNode类
*/
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
// write code here
struct ListNode* slow = pListHead;
struct ListNode* fast = pListHead;
//空链表
if (pListHead == NULL) {
return NULL;
}
while (k > 0) {
//快指针为空,返回空
if (fast == NULL)
return NULL;
fast = fast->next;
k--;
}
while (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
return slow;
}
3.5 合成链表
合并两个有序链表：https://leetcode.cn/problems/merge-two-sorted-lists/description/
将两个列表的元素挨个比较，较小的插入新链表。首先需要判断两个链表中可能有一个或两个链表都为空的情况，如果其中一个是空链表，直接返回另一个即可。在插入的过程中需要判断是不是第一个节点的情况，也就是新链表第一次插入。最后有一个链表迭代后为空时，需要将尾巴与另一个链表连接上
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
//如果有一个链表为空,返回另一个
if(list1 == NULL)
return list2;
if(list2 == NULL)
return list1;
struct ListNode* newnode = NULL;
struct ListNode* tail = NULL;
while (list1 != NULL && list2 != NULL) {
if (list1->val <= list2->val) {
//是不是第一个节点
if (tail == NULL) {
newnode = list1;
tail = list1;
} else {
tail->next = list1;
tail = list1;
}
list1 = list1->next;
} else {
//同上
if (tail == NULL) {
newnode = list2;
tail = list2;
} else {
tail->next = list2;
tail = list2;
}
list2 = list2->next;
}
}
//一个链表走完,链接另一个
if (list1 == NULL) {
tail->next = list2;
}
if (list2 == NULL) {
tail->next = list1;
}
return newnode;
}
3.6 链表分割
链表分割https://www.nowcoder.com/practice/0e27e0b064de4eacac178676ef9c9d70?tpId=8&&tqId=11004&rp=2&ru=/activity/oj&qru=/ta/cracking-the-coding-interview/question-ranking
约瑟夫环，所与人围成一个圈，数到3或数到4的人自杀，什么位置才能让自己幸存到最后一个
用数组解决，挪动删除比较麻烦，所以可以直接用标记-1为已经删除的。这种更适合用链表做，删除必剪方便
思路
可以用两个链表，为了保证数据的顺序不变，将这个值大和小的节点分别尾插到两个链表。在最后，要把后面的链表尾置空，不然会循环起来。可以设置哨兵位，也可以不设置，头节点的尾插会方便很多
不带哨兵位
ListNode* partition(ListNode* pHead, int x) {
// write code here
//记录链表头和当前链表尾
ListNode* list1 = NULL;
ListNode* cur1 = NULL;
ListNode* list2 = NULL;
ListNode* cur2 = NULL;
ListNode* cur = pHead;
while (cur != NULL) {
//插入第一个链表
if (cur->val < x) {
//第一次插入
if (list1 == NULL) {
list1 = cur;
} else {
cur1->next = cur;
}
cur1 = cur;
} else {
if (list2 == NULL) {
list2 = cur;
} else {
cur2->next = cur;
}
cur2 = cur;
}
cur = cur->next;
}
//链表为空的三种情况,分别将尾节点置空
if (list1 == NULL) {
cur2->next = NULL;
return list2;
} else if (list2 == NULL) {
cur1->next = NULL;
return list1;
} else {
cur1->next = list2;
cur2->next = NULL;
return list1;
}
}
带哨兵位
ListNode* partition(ListNode* pHead, int x) {
// write code here\
//两个链表的哨兵位和尾结点,哨兵位不存数据
ListNode* head1 = NULL;
ListNode* head2 = NULL;
ListNode* tail1 = NULL;
ListNode* tail2 = NULL;
head1 = tail1 = (ListNode*)malloc(sizeof(struct ListNode));
head2 = tail2 = (ListNode*)malloc(sizeof(struct ListNode));
ListNode* cur = pHead;
while (cur != NULL) {
//判断大小插入哪个链表
if (cur->val < x) {
tail1->next = cur;
tail1 = cur;
} else {
tail2->next = cur;
tail2 = cur;
}
cur = cur->next;
}
//链接两个链表
tail1->next = head2->next;
//尾结点置空
tail2->next = NULL;
//更新头节点到第一个链表
pHead = head1->next;
//释放资源
free(head1);
free(head2);
return pHead;
}
3.7 回文结构
链表的回文结构：https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa?tpId=49&&tqId=29370&rp=1&ru=/activity/oj&qru=/ta/2016test/question-ranking
思路
先找到链表的中间节点将后面的逆置，从中间节点开始和头部不断向后比。可以利用前面做过的逆置和中间节点的题
struct ListNode* middleNode(struct ListNode* head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
while (fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
struct ListNode* reverseList(struct ListNode* head) {
struct ListNode* newhead = NULL;
struct ListNode* cur = head;
while (cur != NULL) {
//记录下一个插入的元素
struct ListNode* next = cur->next;
//头插
cur->next = newhead;
//移动头节点
newhead = cur;
//迭代
cur = next;
}
return newhead;
}
bool chkPalindrome(ListNode * A) {
// write code here
ListNode* mid = middleNode(A);
ListNode* rmid = reverseList(mid);
ListNode* fast = A;
while (rmid != NULL) {
if(A->val != rmid->val)
return false;
//迭代
A= A->next;
rmid = rmid->next;
}
return true;
}
3.8 相交
相交链表：https://leetcode.cn/problems/intersection-of-two-linked-lists/description/
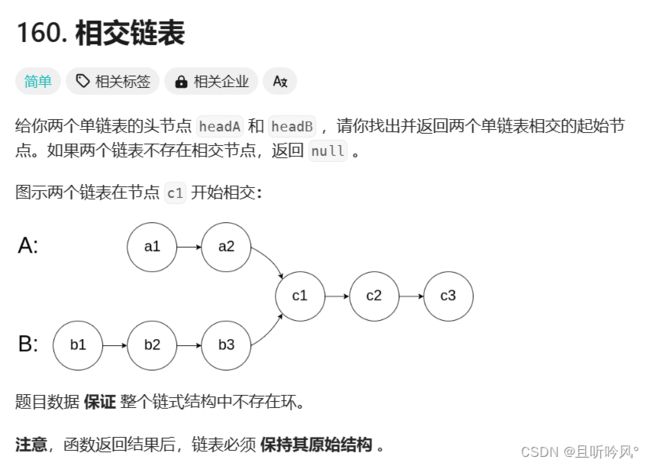
思路
如何判断两个链表有没有相交，可以看两个链表的尾节点是不是一样，因为一个节点不能指向两个节点，所以相交的链表尾结点是一样的。计算出两个链表的长度，让长的链表先走两个的差值，这样再同时走就能找到相交的节点了
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
//记录尾结点
struct ListNode * tail1 = headA;
struct ListNode * tail2 = headB;
//记录长度
int len1 = 0;
int len2 = 0;
//题干链表不是空链表,所以可以直接判断下一个节点
while(tail1->next != NULL)
{
tail1 = tail1->next;
len1++;
}
while(tail2->next != NULL)
{
tail2 = tail2->next;
len2++;
}
//有没有交点
if(tail1 != tail2)
{
return NULL;
}
int gap = abs(len1 - len2);
//短的移动
struct ListNode * shortlist = headA;
struct ListNode * longlist = headB;
while(gap--)
{
if(len1 > len2)
shortlist = shortlist->next;
else
longlist = longlist->next;
}
//找交点返回
while(shortlist != longlist)
{
shortlist = shortlist->next;
longlist = longlist->next;
}
return shortlist;
}
3.9 环形链表
是否环形: https://leetcode.cn/problems/linked-list-cycle/description/
分析
环形链表的一些图示
当进入到环形里就会不断绕着环转圈，要想看是不是环形链表，就看它遍历后的节点是否会重复，直接判断有些麻烦。可以用快慢指针，如果是环形，快指针肯定会和慢指针相遇，快指针可以一次走n步，每走一步判断是否和慢指针相等。为了方便，这里快指针一次走两步，原因在下面说明
bool hasCycle(struct ListNode *head) {
struct ListNode * slow =head;
struct ListNode * fast = head;
//走到空或只有一个节点结束
while(fast != NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
return true;
}
return false;
}
为什么快指针走两步，慢指针走一步就可以
当链表是有环的，快指针先进环，慢指针后进环。当慢指针刚进时，就可能相遇，最差的情况两个指针距离刚好走了环的长度。假设两个指针都进环时距离是N，快指针每走两步就是N+2,慢指针就是N+1，两个相减后，就是距离缩小了一步，这样循环下去，总会有追上的时候
如果快指针走N步，3步5步行不行
这种情况就会有可能一直追不上，还是上面的N，N+3减去N+1，走3步距离每次缩小两步，当之间的距离只有一步时，如果不是快指针每走一步就判断的话就会错过。因为他们的距离每次缩短N-2，可能会越过某一点。就会分环内总长度是奇数还是偶数，如果是奇数，就可能会一直错过
3.10 环链表环节点
返回环形链表入环第一个节点：https://leetcode.cn/problems/linked-list-cycle-ii/description/
思路
第一种:
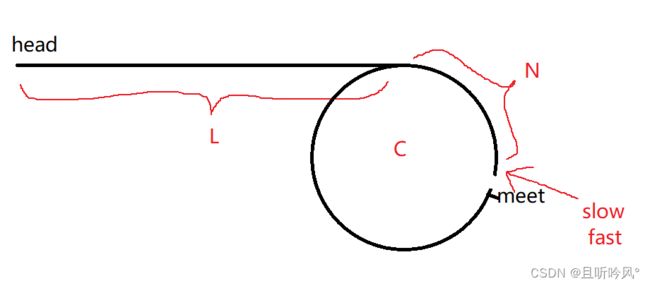
假设快指针每次走两步，慢指针每次走一步。链表头到入环点的距离为L，环型的长度是C，慢指针入环后走的距离是N，慢指针走的总路程L + N，因为不存在会错过的情况，所以快指针必然在一圈内追上慢指针。快指针总路程为L + n * C + N，快指针在相遇时可能已经走了n圈，下图所示：
因为每次走两步，所以快指针的总路程是慢指针的2倍，所以有公式：
2（L+N）= L+N+nC
L和N移到左边减去有：
L+N = n C
L = n*C - N
可以理解为: L=(n-1) * (C- N)
C-N的部分刚好是入口点到meet的长度，所以L的长度和meet移动C-N后刚好是入口点
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode * slow =head;
struct ListNode * fast = head;
//走到空或只有一个节点结束
while(fast != NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
//定义相遇节点
struct ListNode * meet = slow;
//没遇到继续走
while(head != meet)
{
meet = meet->next;
head = head->next;
}
return meet;
}
}
return false;
}
第二种思路：
将环内从meet的next处断开，看为新的链表头，和head这个链表找交点，就是入口点
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode * slow =head;
struct ListNode * fast = head;
//走到空或只有一个节点结束
while(fast != NULL && fast->next != NULL)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
//定义新链表,尾节点为slow
struct ListNode * meet = slow->next;
struct ListNode * tail1 = meet;
int len1 = 0;
//长链表先走
while(tail1 != slow)
{
tail1 = tail1->next;
len1++;
}
struct ListNode * tail2 = head;
int len2 = 0;
while(tail2 != slow)
{
tail2 = tail2->next;
len2++;
}
int gap = abs(len1 - len2);
while(gap--)
{
if(len1 > len2)
{
meet = meet->next;
}
else{
head = head->next;
}
}
//同时走找第一个交点
while(head != meet)
{
head =head->next;
meet= meet->next;
}
return meet;
}
}
return NULL;
}