力扣hot100

最小栈

Deque<Integer> stack1;
 Deque<Integer> stack2;
   public void pop() {
     //这里如果用==比较是比较两个Integer对象的地址,Integer能缓存(-128,127)这个范围的值的Integer对象，用==比较这个范围的值会返回true,超过这个范围用==比较就是不同的对象返回false,所以要equals进行比较,equals直接比较数值不比较地址   
     if (stack1.peek() == stack2.peek()) {
       stack1.pop();
       stack2.pop();
     } else {
       stack1.pop();
    }
 }

public boolean equals(Object obj) {
    if (obj instanceof Integer) {
        return value == ((Integer)obj).intValue();
    }
    return false;
}

比特位计数
暴力法

public int[] countBits(int n) {
        int[] res = new int[n+1];
        for (int i = 0; i <= n; i++) {
            int mask = 1;
            int count = 0;
            for (int j = 0; j < 32; j++) {
                if ((mask & i) != 0) {
                    count++;
                }
                mask <<= 1;
            }
            res[i] = count;
        }
        return res;
    }

动态规划法

public int[] countBits(int n) {
        int[] res = new int[n+1];
        res[0] = 0;
        for (int i = 1; i <= n; i++) {
            //奇数的话1的位数就比前一个数多1
            if (i % 2 == 1) {
                res[i] = res[i-1] + 1;
            } else {
            //偶数的话1的位数就和除于2之后的位数一样
                res[i] = res[i/2];
            }
        }
        return res;
}

汉明距离
用异或，先x和y异或，不相等为1，然后再和1进行与

//左移找1
public int hammingDistance(int x, int y) {
        int mask = 1;
        int res = 0;
        for (int i = 0 ; i < 32 ; i++) {
            if ((mask & (x ^ y)) == mask) {
                res++;
            }
            mask <<= 1;
        }
        return res;
}
//右移找1
public int hammingDistance(int x, int y) {
        int res = 0;
        int s = x ^ y;
        while (s != 0) {
            if ((s & 1) == 1) {
                res++;
            }
            s >>= 1;
        }
        return res;
    }

二叉树的直径
求每个节点的左子树最大值+右子树最大值，然后最大的就是结果

   int res = 0;
    public int diameterOfBinaryTree(TreeNode root) {
         depth(root);
         return res;
    }

    public int depth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = depth(root.left);//左子树最大值
        int rightDepth = depth(root.right);//右子树最大值
        res = Math.max(leftDepth + rightDepth,res);//更新结果
        return 1 + Math.max(leftDepth,rightDepth);
    }

合并二叉树
同时遍历两个二叉树，如果其中一个为空就返回另一个

 public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null && root2 == null) {
            return null;
        }
        TreeNode root = new TreeNode(0);
        if (root1 != null) {
            root.val += root1.val;
        }
        if (root2 != null) {
            root.val += root2.val;
        }
        //root1 == null这个判断是为了防止root1.left报空指针异常
        root.left = mergeTrees(root1 == null ? null : root1.left,root2 == null ? null : root2.left);
        root.right = mergeTrees(root1 == null ? null : root1.right,root2 == null ? null : root2.right);
        return root;
    }

搜索旋转排序数组
数组nums[6,7,0,1,2,4,5] target为0

第一轮循环：left = 0，right = 6 ，mid = 3，nums[left] = 6,nums[right] = 5,nums[mid] = 1
nums[mid]为1, 比nums[rihgt]小，nums[mid]到nums[rihgt]是有序的,不过target没有大于nums[mid] 和小于等于nums[right]，所以不在【nums[mid+1],nums[right]】这个区间，所以target在【nums[left],nums[mid-1]】这个区间

第二轮循环：left = 0，right = 2 ，mid = 1，nums[left] = 6,nums[right] = 0,nums[mid] = 7
nums[mid]为7，比nums[rihgt]大，nums[left]到nums[mid]是有序的,不过target没有大于等于nums[left] 和小于nums[mid]，所以不在【nums[left],nums[mid-1]】这个区间,所以target在【nums[mid+1],nums[right]】这个区间

第三轮循环：left = 2, right = 2，mid = 2，nums[left] = 0,nums[right] = 0,nums[mid] = 0
nums[mid]为0等于target退出循环返回下标

public int search(int[] nums, int target) {
        int len = nums.length;
        if (len == 0) {
            return -1;
        }
        int left = 0,right = len - 1;
        while (left <= right) {
            int mid = (left + right)/2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < nums[right]){
                //此时target在[mid+1,right]这个区间
                if (nums[mid] < target && target <= nums[right]) {
                    left = mid + 1;
                } else {
                    //否则target就在[left,mid-1]这个区间
                    right = mid - 1;
                }
                //mid比right大即前半段有序
            } else {
                //此时target在[left,mid-1]这个区间
                if (nums[left] <= target && target < nums[mid]) {
                    right = mid - 1;
                } else {
                //否则target就在[mid+1,right]这个区间
                    left = mid + 1;
                }
            }
        }
        return -1;
    }

下一个更大的排列
从数组倒着查找，找到nums[i] 比nums[i+1]小的时候，就将nums[i]跟nums[i+1]到nums[nums.length - 1]当中找到一个最小的比nums[i]大的元素交换。交换后，再把nums[i+1]到nums[nums.length-1]排序

 * 1、从后向前查找第一个相邻升序的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
 * 2、在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
 * 3、将 A[i] 与 A[k] 交换
 * 4、可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
 * 5、如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4

例如12385764，从4开始往前找第一个相邻升序的元素对 (i,j)，找到（5,7）【7,4】一定是降序，
在【7,4】这个区间从后向前找第一个比5大的找到6，然后5和6交换变成12386754，最后把【7,4】这个区间的数改为降序就变成12386457就是下一个更大的排序

public void nextPermutation(int[] nums) {
        int k = 0;
        int length = nums.length;
        for (int i = length - 1; i > 0; i--) {
            //找到相邻升序元素对
            if (nums[i - 1] < nums[i]) {
                //在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k
                for (int j = length - 1; j >= i; j--) {
                    if (nums[j] > nums[i - 1]) {
                        k = j;
                        break;
                    }
                }
                //将 A[i] 与 A[k] 交换
                int temp = nums[i-1];
                nums[i-1] = nums[k];
                nums[k] = temp;
                //逆置 [j,end)，使其升序
                Arrays.sort(nums,i,length);
                return;
            }
        }
        Arrays.sort(nums);
    }

无重复字符的最长子串
没遇到重复字符，滑动窗口的起始位置为0,然后和之前滑动窗口的起始位置比较，取较大值
遇到重复字符，滑动窗口的起始位置为重复字符上次出现的位置+1,然后和之前滑动窗口的起始位置比较，取较大值，最长子串为当前遍历字符-滑动窗口起始位置+1

例如遍历aabba
遍历a，还没出现过，滑动窗口起始位置为0，最长子串为0-0+1=1
遍历a，遇到重复字符，滑动窗口的起始位置为重复字符上次出现的的位置+1即0+1=1，和之前滑动窗口的起始位置比较，1比0大取1，最长子串为1-1+1=1
遍历b，还没出现过，滑动窗口起始位置为0，和之前滑动窗口的起始位置比较,0比1小取1，最长子串为,2-1+1=2
遍历b，遇到重复字符，滑动窗口的起始位置为重复字符上次出现的的位置+1即2+1=3，和之前滑动窗口的起始位置比较，3比1大取3，最长子串为3-3+1=1
遍历a，遇到重复字符，滑动窗口的起始位置为重复字符上次出现的的位置+1即1+1=2，和之前滑动窗口的起始位置比较，2比3小取3，最长子串为4-3+1=2,此时a为最后一个字符，遍历结束
滑动窗口的起始位置开始后面都不会有重复元素

 public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) {
            return 0;
        }
        if (s.length() == 1) {
            return 1;
        }
        Map<Character, Integer> charMap = new HashMap<>();
        int res = 0;
        int start = 0;
        char[] chars = s.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            //最后一次出现的位置
            int preIndex = charMap.getOrDefault(chars[i],-1);
            //滑动窗口的开始位置，这个位置开始后面都不会有重复元素
            start = Math.max(start,preIndex + 1);
            res = Math.max(res,i - start + 1);
            charMap.put(chars[i],i);
        }
        return res;
    }

另一种解法
不断向右扩大窗口，直到遇到重复字符，然后向右缩小窗口直到没有重复字符，然后继续向右扩大窗口，遇到重复字符就继续缩小窗口，如此重复直到窗口扩大到最后一个字符
窗口没有重复字符就更新一次结果为窗口大小
例如aabba
向右扩大窗口变成a（没有重复字符更新结果为1）,
aa遇到重复字符，然后向右缩小窗口变成a没有重复字符（更新结果为1），
然后继续向右扩大窗口变成ab（没有重复字符更新结果为2），abb遇到重复字符，向右缩小窗口变成bb,b没有重复字符（没有重复字符更新结果为1），
继续向右扩大窗口变成ba（没有重复字符更新结果为2），窗口扩大大最后一个字符结束遍历

public int lengthOfLongestSubstring1(String s) {
        //v为字符出现的次数
        Map<Character, Integer> charMap = new HashMap<>();
        int left = 0,right = 0,res = 0;
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            //记录字符出现次数
            charMap.merge(c, 1, Integer::sum);
            //判断窗口是否要向右收缩，当前字符重复了就要向右收缩直到不重复
            while (charMap.get(c) > 1) {
                char c1 = s.charAt(left);
                //窗口向右缩小
                left++;
                //左指针所指字符出现次数-1
                charMap.put(c1,charMap.get(c1) - 1);
            }
            //更新结果
            res = Math.max(res,i - left + 1);
        }
        return res;
    }

合并区间
如果当前区间的左端点比数组 merged 中最后一个区间的右端点小，那么它们不会重合，我们可以直接将这个区间加入数组 merged 的末尾；
否则，它们重合，我们需要用当前区间的右端点更新数组 merged 中最后一个区间的右端点，将其置为二者的较大值。
例如要合并的区间为{{1, 3}, {2, 6}, {8, 10}, {15, 18}};
merged现在是【1，3】，当前遍历区间是【2,6】，3和2比较，3比2大，存在交集，要更新【1,3】的右端点，取3，6的较大值，更新为【1，6】
merged现在是【1，6】，当前遍历区间是【8,10】，6和8比较，6比8小，不存在交集，直接把区间加到
merged 的末尾变成【1,6】【8,10】

每次都是数组 merged 中最后一个区间的右端点和当前区间的左端点比是因为数组 merged 中最后一个区间的右端点肯定是数组 merged里最大的，如果当前区间的左端点比这个右端点大，即当前区间是大于
数组 merged所有数的，不存在交集，如果果当前区间的左端点比这个右端点小，即当前区间和数组 merged出现交集，有可能是都小于数组 merged右端点，有可能一部分小于数组 merged右端点，要看数组 merged右端点和当前区间的右端点哪个大，如果 merged右端点大，即都小于右端点，如果当前区间的右端点大，即一部分小于数组 merged右端点

public int[][] merge(int[][] intervals) {
        int len = intervals.length;
        if (len < 2) {
            return intervals;
        }
        // 按照起点排序，根据每个区间的左端点排序
        Arrays.sort(intervals, Comparator.comparingInt(o -> o[0]));
        // 也可以使用 Stack，因为我们只关心结果集的最后一个区间
        List<int[]> res = new ArrayList<>();
        res.add(intervals[0]);
        for (int i = 1; i < len; i++) {
            int[] curInterval = intervals[i];

            // 每次新遍历到的列表与当前结果集中的最后一个区间的末尾端点进行比较
            int[] peek = res.get(res.size() - 1);

            //当前遍历区间左边端点比结果集最后一个区间的末尾端点大相当于没有出现交集
            if (curInterval[0] > peek[1]) {
                res.add(curInterval);
            } else {
                // 注意，这里出现交集应该取最大
                //例如【1,4】【2,3】3比4大合并区间变成【1,3】 【1,3】【2,6】 3比6小合并区间变成【1,6】
                peek[1] = Math.max(curInterval[1], peek[1]);
            }
        }
        return res.toArray(new int[res.size()][]);
    }

组合总和
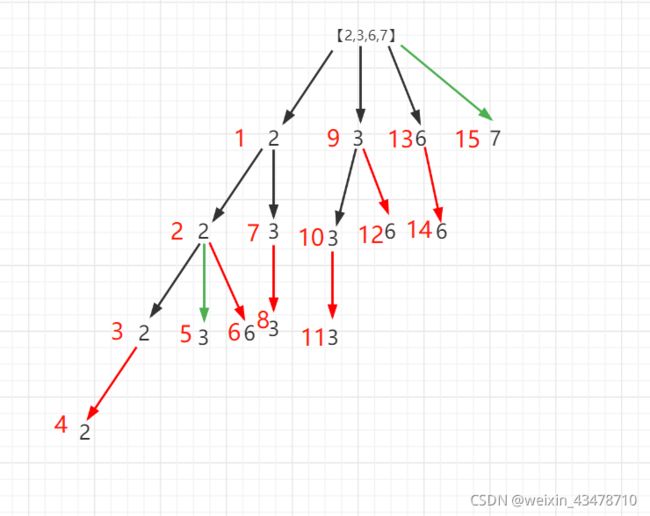
用回溯把所有的路径列出来，这里的是组合，元素不能重复，例如出现了1,2就不能出现2,1，代码是用一个start变量实现，例如start为0只能遍历大于等于0的元素，start为1只能遍历大于等于1的元素

【2,3,6,7】 target为7
红色箭头表示当前递归比target要大，终止当前递归，即剪枝， 后面的数都不会遍历，例如第4步【2,2,2,2】比7大，然后不会有【2,2,2,3]绿色箭头表示找到的结果返回，红色数字表示访问顺序

public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> list = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        Arrays.sort(candidates);
        combinationSumDfs(candidates,target,0,list,path);
        return list;
    }

private void combinationSumDfs(int[] candidates, int target, int start, List<List<Integer>> list, List<Integer> path) {
        if (target == 0) {
            list.add(new ArrayList<>(path));
            return;
        }
        for (int i = start; i < candidates.length; i++) {
        //break是终止递归，返回上一层循环，return是终止递归，继续当前循环
            if (target - candidates[i] < 0) {
                break;
            }
            path.add(candidates[i]);
            combinationSumDfs(candidates,target - candidates[i],i,list,path);
            path.remove(path.size() - 1);
        }
    }

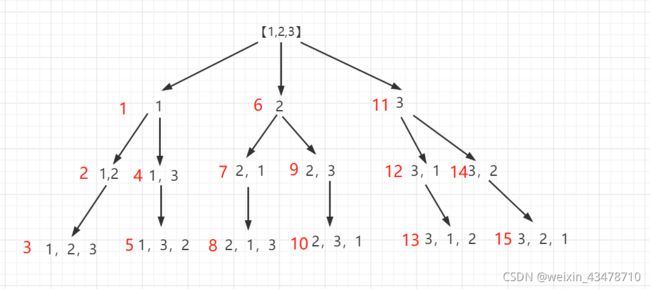
全排列
排列是顺序不同元素可以重复，例如出现了1,2，也可以出现2,1
要用一个数组判断当前元素是否被访问过

 private List<List<Integer>> list = new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        int length = nums.length;

        if (length == 0) {
            return list;
        }
        Arrays.sort(nums);
        List<Integer> path = new ArrayList<>();
        boolean[] used = new boolean[length];
        permuteDfs(nums,0,used,length,path);
        return list;
    }

    private void permuteDfs(int[] nums, int index, boolean[] used, int length, List<Integer> path) {
        if (index == length) {
            list.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < length; i++) {
            if (!used[i]) {
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteDfs(nums,index + 1,used,length,path);
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }

跳跃游戏
顺着推（贪心）：
每次遍历都看最远距离能否到当前位置，以及当前位置能跳到多远

 public boolean canJump(int[] nums) {
        int farthest = 0;

        for (int i = 0; i < nums.length - 1; i++) {
            //跳的最远距离能否到达当前位置
             if (i <= farthest) {
                 farthest = Math.max(farthest,i + nums[i]);
            }
           
        
        }
        return farthest >= nums.length - 1;
    }

逆着推（动态规划）：
从倒数第二位开始推，看倒数第二位能否到达倒数第一位
然后看倒数第三位能否到达倒数第二位
如此类推直到第一位能否到达第二位

public boolean canJump(int[] nums) {
        
        if (nums == null) {
            return false;
        }
        boolean[] dp = new boolean[nums.length];
        dp[0] = true;
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                // 如果之前的j节点可达，并且从此节点可以到跳到i
                if (dp[j] && nums[j] + j >= i) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[nums.length - 1];
    }

不同路径
当前位置的路径数等于左边位置的路径数+上边位置的路径数
dp【i】【j】 = dp【i-1】【j】 + dp【i】【j-1】

public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
//        uniquePathsDfs(matrix,0,0);
        Arrays.fill(dp[0], 1);
        for (int i = 0; i < dp.length; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i < dp.length; i++) {
            for (int j = 1; j < dp[0].length; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }

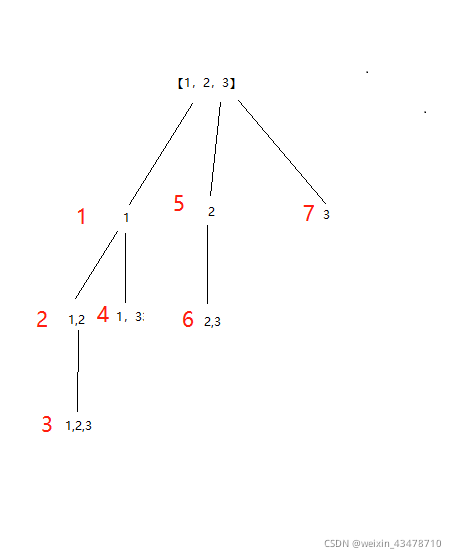
子集
用回溯找出所有子集，包括空集，这个是组合，元素不能有重复

List<List<Integer>> subsets = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        List<Integer> path = new ArrayList<>();
        subsets.add(new ArrayList<>());
        subsetsDfs(nums,path,0);
        return subsets;
    }

    public void subsetsDfs(int[] nums, List<Integer> path, int start) {
        if (path.size() == nums.length) {
            return;
        }
        for (int i = start; i < nums.length; i++) {
            path.add(nums[i]);
            System.out.println(path.toString());
            subsets.add(new ArrayList<>(path));
            subsetsDfs(nums,path,i+1);
            path.remove(path.size() - 1);
        }
    }

验证二叉搜索树
中序遍历，用一个pre变量保存前一个遍历的节点的值，如果该值比当前遍历的节点的值小就不是二叉搜索树

long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (!isValidBST(root.left)) {
            return false;
        }
        //当前节点小于前一个节点就不符合bst
        if (root.val < pre) {
            return false;
        }
        pre = root.val;
        return isValidBST(root.right);
    }

从前序与中序遍历序列构造二叉树
用一个map记录中序遍历序列节点和节点对应的索引
递归函数（前序遍历序列，当前子树根节点索引（对应前序遍历索引），中序遍历序列左边界，中序遍历序列右边界）

[3,9,20,15,7]
[9,3,15,20,7]
3是当前子树根节点索引，这个节点在中序遍历排第2位，中序遍历这个节点左边的节点都是这个节点的左子树，即9是3的左子树，这个节点右边的节点都是这个节点的右子树，即15,20,7是这个节点的右子树
左子树的根节点是左子树的前序遍历的第一位，即当前子树根节点索引的后一位是9
右子树的根节点是右子树的前序遍历的第一位，即当前子树根节点索引+左子树节点数量+1，左子树节点数量为左子树右边界-左边界+1，左子树右边界为0，左边界为0，0-0+1=1即左子树节点数量，右子树的根节点为0（当前子树根节点索引）+1(左子树节点数量)+1=2,即20是右子树的根节点
所以当前子树根节点为3，左子树为9，右子树为20

左子树：root->left = pre_order(前序左子树范围，中序左子树范围，前序序列，中序序列);；
右子树：root->right = pre_order(前序右子树范围，中序右子树范围，前序序列，中序序列);。

简单来说就是每次递归找出左子树的前序遍历范围，右子树的前序遍历范围，左子树的中序遍历范围，右子树的中序遍历范围，然后根据前序遍历的第一个节点构造根节点，左子树的中序遍历范围的作用是算出左子树的节点数量

Map<Integer, Integer> map = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i],i);
        }
        return buildTreeDfs(preorder,0,0,preorder.length - 1);
    }

    public TreeNode buildTreeDfs(int[] preorder, int preRootIndex, int left, int right) {
        if (left >= right) {
            return new TreeNode(preorder[left]);;
        }
        TreeNode root = new TreeNode(preorder[preRootIndex]);
        int inoderIndex = map.get(preorder[preRootIndex]);
        //右子树的根节点索引等于根节点索引+左子树节点数（左子树右边界-左边界+1）+1
        int leftNum = inoderIndex - left;
        root.left = buildTreeDfs(preorder,preRootIndex + 1,left,inoderIndex - 1);
        root.right = buildTreeDfs(preorder,preRootIndex + leftNum + 1,inoderIndex + 1, right);
        return root;
    }

最长连续序列
用一个set记录数组里的数，遍历时看当前数的前一位有没有出现过，没出现过当前数自己就是最长连续序列即1，出现过再往后找，直到没出现过
例如[100,4,200,1,3,2]
遍历100，看99有没出现过，没出现过最长连续序列为1
遍历4，看4有没出现过，出现过最长连续序列为2
遍历200，看199有没出现过，没出现过最长连续序列为1
遍历1，看0有没出现过，没出现过最长连续序列为1
遍历3，看2有没出现过，出现过，直到找到5没出现过最长连续序列为3
遍历2，看1有没出现过，出现过，直到找到5没出现过最长连续序列为4

 public int longestConsecutive(int[] nums) {
Set<Integer> numSet = new HashSet<>();
        for (int num : nums) {
            numSet.add(num);
        }
        int longestLength = 0;
        for (int num : numSet) {
            //如果前一个元素不存在就从当前元素开始算
            if (!numSet.contains(num-1)) {
                int cur = num;
                int curLength = 1;
                while (numSet.contains(cur+1)) {
                    cur++;
                    curLength++;
                }
                longestLength = Math.max(longestLength,curLength);
            }
        }
        return longestLength;
    }

颜色分类
就是把数字分成三块，比1小的在左边，比1大的在右边，等于1的在中间类似于快速排序，不过这里不用递归

 public void sortColors(int[] nums) {
        int i = 0,j = nums.length - 1,base = 1,cur = 0;
        while (cur <= j) {
            if (nums[cur] < base) {
                swap(nums,i,cur++);
                i++;
//                swap(nums,i++,cur++);
            } else if (nums[cur] > base) {
                //j最后停留在第一个大于1的前一位
                swap(nums,j,cur);
                j--;
//                swap(nums,--j,cur);//--j j最后停留在第一个大于1的,使用--j,j的初始值要为nums.length
            } else {
                cur++;
            }
        }
    }

单词拆分
用动态规划
状态转移方程：
dp[right] 表示 s 的前 right位是否可以用wordDict中的单词表示
dp[right] = dp[left] && subString(left+1,right+1)
字符串“leetcode”,单词列表“leet”,“code”
right等于3时， subString(0,4)为leet在单词列表里，所以dp[right]=dp[3]=true
right等于7时， subString(4,8)为code在单词列表里，dp[3] = true, dp[3] && subString(4,8)等于true,所以dp[7]=true

 public boolean wordBreak(String s, List<String> wordDict) {
        Set<String> wordSet = new HashSet<>(wordDict);
        int len = s.length();

        // 状态定义：以 s[i] 结尾的子字符串是否符合题意
        boolean[] dp = new boolean[len];
        for (int right = 0; right < len; right++) {
            // 分类讨论 1：不拆分，substring 右端点不包含，所以是 right + 1
            if (wordSet.contains(s.substring(0, right + 1))) {
                dp[right] = true;
                continue;
            }
            // 分类讨论 2：拆分
            // right等于4是看c tc etc eetc left大于等于0是因为上面的if已经算出了0到right的
            // right等于4先算leetc是否包含在wordSet里，不包含就在算c tc etc eetc是否包含在wordSet里
            // 如果tc包含在wordSet里，就看lee是否包含在wordSet里，如果包含的话即leetc都包含在wordSet里，可以被拆分
            for (int left = right - 1; left >= 0; left--) {
                System.out.println(s.substring(left + 1, right + 1));
                if (wordSet.contains(s.substring(left + 1, right + 1)) && dp[left]) {
                    dp[right] = true;
                    // 这个 break 很重要，一旦得到 dp[right] = True ，循环不必再继续
                    break;
                }
            }
        }
        return dp[len - 1];
    }

LRU 缓存机制
用map和双向链表实现，get和put一个key时把key加到队尾，队尾的是最近使用，缓存满了把队头的元素删除，然后把key加到队尾，只需要新增key时判断缓存是否满

class LRUCache {

    int cap, size;
    Node1 head, tail;
    Map<Integer,Node1> cache = new HashMap<>();
    LRUCache(int capacity) {
        this.size = 0;
        this.cap = capacity;
        head = new Node1();
        tail = new Node1();
        head.next = tail;//头指向尾
        tail.prev = head;//尾指向头
    }

    class Node1 {
        public int key, val;
        public Node1 next, prev;
        public Node1(){}
        public Node1(int k, int v) {
            this.key = k;
            this.val = v;
        }
    }

    //key不存在时用，即新增
    public void addToTail(Node1 x) {
        x.prev = tail.prev;//x指向尾结点的前一个节点，即倒数第二个节点，x的前驱
        x.next = tail;//x指向尾结点，x的后继
        tail.prev.next = x;//倒数第二个节点指向x,倒数第二个节点的后继
        tail.prev = x;//尾结点指向x,尾结点的前驱
        size++;
    }

    //key存在时用,即更新
    public void moveToTail(Node1 x) {
        removeNode(x);//删除原有的
        addToTail(x);
    }


    public void removeNode(Node1 x) {
            x.prev.next = x.next;//x的前驱节点指向x的后继节点
            x.next.prev = x.prev;//x的后继节点指向x的前驱节点
            size--;
    }

    public Node1 removeHead() {
            if (head.next == null) {
                return null;
            }
            Node1 first = head.next;
            removeNode(head.next);
            return first;
    }

    public int get(int key) {
        if (cache.containsKey(key)) {
            Node1 node1 = cache.get(key);
            moveToTail(node1);//更新为最近使用
            return node1.val;
        }
        return -1;
    }

    public void put(int key, int val) {
        //存在key,更新value,把当前key变成最近使用的
        if (cache.containsKey(key)) {
            //更新
            Node1 node1 = cache.get(key);
            node1.val = val;
            moveToTail(node1);
        } else {
            Node1 node1 = new Node1(key, val);
            cache.put(key,node1);
            if (size >= cap) {
                Node1 first = removeHead();
                cache.remove(first.key);
                
            }
            addToTail(node1);
        }
    }

}

排序链表
自底向上排序
4->2->3->1,先排4和2、3和1排序之后结果为2->4->1->3
具体步骤是断开4和2，变成两个链表然后再按照顺序合并变成2->4
断开3和1，变成两个链表然后再按照顺序合并变成1->3
再排2，4和1,3排序之后结果为1->2->3->4
具体步骤是断开2，4和1，3,变成两个链表然后再按照顺序合并变成1->2->3->4

 //自底而上合并
    public ListNode sortList(ListNode head) {
        ListNode dummy = new ListNode(Integer.MIN_VALUE);
        dummy.next = head;
        ListNode temp = dummy.next;
        int length = 0;
        while (temp != null) {
            length++;
            temp = temp.next;
        }
        for (int size = 1; size < length; size *= 2) {
            ListNode cur = dummy.next;
            ListNode tail = dummy;//tail的作用是用来标记每次已排序的尾部,此时还没开始排序，所以tail是哨兵节点
            //开始切割和合并
            while (cur != null) {
                //切之前的
                ListNode left = cur;
                //切一次变成4->null 2->3->1->>null
                ListNode right = cut(left,size);
                //再切一次变成4->null 2->null 3->1->>null
                cur = cut(right,size);
                //合并4->null和2->null
                tail.next = mergeList(left,right);
                while (tail.next != null) {
                    tail = tail.next;//此时tail是2
                }
            }
        }
        return dummy.next;
    }

    //返回切之后的右边节点
    public ListNode cut(ListNode before, int cutSize) {
        if (cutSize < 0) {
            return before;
        }
        ListNode temp = before;
        while (cutSize != 1 && temp != null) {
            temp = temp.next;//最终停在切割点的前一位，例如在4->2之间切断，停在4
            cutSize--;
        }

        if (temp == null) {
            return null;
        }

        ListNode after = temp.next;//切掉后的右边节点
        temp.next = null;//断开左边的节点和右边的节点 4->2->1->3->null变成 4->null
        return after;
    }

    public ListNode mergeList(ListNode list1, ListNode list2) {
        ListNode dummy = new ListNode();
        ListNode cur = dummy;
        while (list1 != null || list2 != null) {
            if (list1 == null) {
                cur.next = list2;
                break;
            } else if (list2 == null) {
                cur.next = list1;
                break;
            } else if (list1.val <= list2.val) {
                cur.next = list1;
                list1 = list1.next;
            } else {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;
        }
        return dummy.next;
    }

最大乘积子数组
遍历的过程中记录最大值和最小值，遍历的数是正数，最大值就是当前数乘以最大值，如果最大值为负数，最大值就是当前数，最小值就是当前数乘以最小值
遍历的数是负数，最大值是当前数乘以最小值，如果最小值就是当前数乘以最大值，如果最大值为负数，最小值是当前数
dp【i】【0】连续子数组的最小值
dp【i】【1】连续子数组的最大值

public int maxProduct(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        int length = nums.length;
        //dp[i][0]连续子数组的最小值
        //dp[i][1]连续子数组的最大值
        int[][] dp = new int[length][2];
        dp[0][0] = nums[0];
        dp[0][1] = nums[0];
        for (int i = 1; i < length; i++) {
            if (nums[i] >= 0) {
                dp[i][0] = Math.min(nums[i],nums[i] * dp[i-1][0]);
                dp[i][1] = Math.max(nums[i],nums[i] * dp[i-1][1]);
            } else {
                //负数时最小值有可能是负数乘以最大值
                dp[i][0] = Math.min(nums[i],nums[i] * dp[i-1][1]);
                //负数时最大值有可能是负数乘以最小值
                dp[i][1] = Math.max(nums[i],nums[i] * dp[i-1][0]);
            }
        }
        int res = dp[0][1];
        for (int i = 1; i < dp.length; i++) {
            if (res < dp[i][1]) {
                res = dp[i][1];
            }
        }
        return res;
    }

自顶向下递归
快慢指针找中点，然后递归切割中点左边和中点右边，切剩一个时终止递归然后开始合并

public ListNode sortList(ListNode head) {
        //只剩一个节点终止递归
        if (head == null || head.next == null) {
            return head;
        }
        ListNode fast = head.next, slow = head;
        //奇数时是fast等于null 偶数时是fast.next等于null
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        //slow是中点，左半段的最后一个节点
        ListNode temp = slow.next;//后半段
        slow.next = null;
        ListNode left = sortList(head);
        ListNode right = sortList(temp);
        ListNode dummy = new ListNode();
        ListNode cur = dummy;
        while (left != null && right != null) {
            if (left.val <= right.val) {
                cur.next = left;
                left = left.next;
            } else {
                cur.next = right;
                right = right.next;
            }
            cur = cur.next;
        }
        cur.next = left == null ? right : left;
        return dummy.next;
    }

打家劫舍
dp[k]=max.(dp[k-1],dp[k-2]+nums[i])
dp[k-1]是当前位置不偷，偷前一位的
dp[k-2]+nums[i]是当前位置偷，然后偷前两位的
[2,7,9,3,1]，1这个位置偷的话，然后3不偷，偷9
1这个位置不偷的话，偷3

public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        if (nums.length == 2) {
            return Math.max(nums[0],nums[1]);
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for (int i = 2; i < nums.length; i++) {
            //当前dp等于max(取当前的数、当前数的前一位就不能取,不取当前数、当前数的前一位就能取)
            dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);
        }
        return dp[nums.length-1];
    }

岛屿数量
遍历数组，遇到1就向四周扩散，直到越界或遇到0，并把访问过的设为2，岛屿数量加1

public int rob(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        if (nums.length == 2) {
            return Math.max(nums[0],nums[1]);
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for (int i = 2; i < nums.length; i++) {
            //当前dp等于max(取当前的数、当前数的前一位就不能取,不取当前数、当前数的前一位就能取)
            dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);
        }
        return dp[nums.length-1];
    }

除自身以外数组的乘积
算出每个数左边的乘积和右边的乘积，然后相乘

public int[] productExceptSelf(int[] nums) {
        int length = nums.length;
        int[] rightMulti = new int[length];
        Arrays.fill(rightMulti,1);
        int[] leftMulti = new int[length];
        int leftRes = 1;
        int rightRes = 1;
        Arrays.fill(leftMulti,1);
        int[] res = new int[length];
        for (int i = 1; i < nums.length; i++) {
            leftRes *= nums[i-1];
            leftMulti[i] = leftRes;
        }
        for (int i = nums.length - 2; i >= 0; i--) {
            rightRes *= nums[i+1];
            rightMulti[i] *= rightRes;
        }
        for (int i = 0; i < nums.length; i++) {
            if (i == 0) {
                res[i] = rightMulti[i];
            } else if (i == nums.length - 1) {
                res[i] = leftMulti[i];
            } else {
                res[i] = leftMulti[i] * rightMulti[i];
            }
        }
        return res;
    }

二叉树的最近公共祖先
后序遍历每个节点的左右子树找p和q,左子树找到p或q，右子树没找到p或q，就返回最先找到的那个，右子树找到p或q，左子树没找到p或q，就返回最先找到的那个，两个子树都找到p和q就返回当前节点
因为是递归，使用函数后可认为左右子树已经算出结果，这句话要记住，道出了递归的精髓

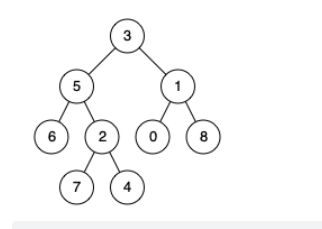
p和q分别是5和4，遍历3的左右子树，左子树先找到p就返回p

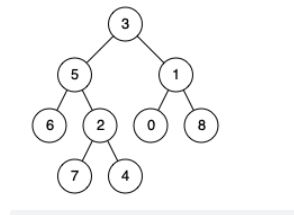
p和q分别是5和1，遍历3的左右子树，左子树找到p，右子树找到q就返回3

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == p || root == q) {
            return root;
        }
        if (root == null) {
            return null;
        }
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if (left == null) {
            return right;
        }
        if (right == null) {
            return left;
        }
        return root;
    }

搜索二维矩阵 II
左下角的元素是当前列最大当前行最小的元素

public boolean searchMatrix(int[][] matrix, int target) {
        int i = matrix.length - 1, j = 0;
        while (j <= matrix[0].length - 1 && i >= 0 ) {
            //目标数比target小就增大，当前位置上边的元素都可以排除掉，因为上边的元素都比当前元素小
            if (matrix[i][j] < target) {
                j++;
            //目标数比target大就减小,当前位置右边的元素都可以排除掉，因为右边的元素都比当前元素大
            } else if (matrix[i][j] > target) {
                i--;
            } else {
                return true;
            }
        }
        return false;
    }

数组中的第K个最大元素
快速排序，每次划分完看标杆索引比目标值索引大还是小，大的话标杆索引就要减小right = index - 1,小的话标杆就要增大left = index + 1

public int findKthLargest(int[] nums, int k) {
        int length = nums.length, res = 0, targetIndex = length - k, left = 0, right = length - 1;
        while (true) {
            int index = quickSort1(nums,left, right);
            if (index == targetIndex) {
                return nums[index];
            } else if (index < targetIndex){
                left = index + 1;
            } else {
                right = index - 1;
            }
        }
    }

    private static Random random = new Random(System.currentTimeMillis());
    private int quickSort1(int[] nums, int left, int right) {
        if (left >= right) {
            return left;
        }
        int i = left, j = right + 1, base = nums(left);
        while (true) {
            while (nums[++i] < base && i < right);//找比base大的
            while (nums[--j] > base && j > left);//找比base小的
            if (i >= j) {
                break;
            }

            if (i <= j) {
               int temp = nums[i];
               nums[i] = nums[j];
               nums[j] = temp;
            }
        }
        //标杆和j换位置
        nums[left] = nums[j];
        nums[j] = base;
        return j;
    }

堆排序
建一个大小为K的小根堆，这个小根堆的元素都是前K大的，堆顶即最小的的那个就是第K大的元素，比K小的元素已经排序好不在堆里了
例如：[3,2,1,5,6,4] 和 k = 2
3加入堆，2加入堆，
1加入堆，堆大小为3比2大，移除堆顶元素1，此时堆的元素为2,3
5加入堆，堆大小为3比2大，移除堆顶元素2，此时堆的元素为3,5
6加入堆，堆大小为3比2大，移除堆顶元素3，此时堆的元素为5,6
4加入堆，堆大小为3比2大，移除堆顶元素4，此时堆的元素为5,6
堆顶元素5为第K大元素

 PriorityQueue<Integer> queue = new PriorityQueue<>(k);
        for (int i = 0; i < nums.length; i++) {
            queue.add(nums[i]);
            if (queue.size() > k) {
                queue.poll();
            } 
        }
        return queue.peek();

背包问题
一般给了一个正整数target，一个数组nums ，然后从数组里取数，凑成一个最大数或最小数一般都是背包问题
数组里的数每个只能取一次是01背包问题，每个能无限取是完全背包问题

1、零钱兑换
总金额为11，硬币有1 2 5，相当于背包容量是11，物品重量是1,2，5，怎样装能用最少的物品装满背包
或者是背包想装的金额为11，物品价值分别是1，2，5，怎样装能用最少的物品装到指定的金额11
dp[i]为容量为i时所需要的最少物品数,dp[i]可能是一个物品放多次变成dp[i]的所以符合完全背包
dp[i] = max(dp[i],dp[i-物品重量]+1）
dp[0]为0
dp[1]为min(dp[1],dp[1-1]+1)
dp[1]为min(dp[1],dp[1-2]+1)，背包容量小于0装不下了跳过
dp[1]为min(dp[1],dp[1-5]+1)，背包容量小于0装不下了跳过

有时会问给出的背包容量可以装到的最大价值

2、完全平方数
完全平方数也是背包问题
当前整数需要的最少完全平方个数 = （当前整数 - 一个完全平方数) 所需要的最少完全平方个数+ 1
dp[i] = min(dp[i],min(dp[i-一个完全平方数]) + 1
例如求dp[12],相当于求dp[12-1],dp[12-2],dp[12-4],dp[12-9]这四个其中的最小值然后+1，+1相当于减去的一个平方数

 //完全平方数就是物品重量（可以无限件使用），凑个正整数n就是背包容量，问装满这个背包最少要多少个物品？
        int[] dp = new int[n + 1];
        Arrays.fill(dp,Integer.MAX_VALUE);
        dp[0] = 0; //0需要0个完全平方数
        for (int i = 1; i <= n; i++) {//背包容量
            for (int j = 1; j * j <= n; j++) {//物品重量
                //当前整数需要的最少完全平方个数 = （当前整数 - 一个完全平方数) + 1
                if (i >= j * j) {
                    dp[i] = Math.min(dp[i],dp[i - j * j] + 1);
                }

            }
        }
        return dp[n];

DFS（记忆化搜索）

Map<Integer,Integer> numSquares = new HashMap<>();
    public int numSquares(int n) {
        if (n == 0) {
            return 0;
        }
        if (numSquares.containsKey(n)) {
            return numSquares.get(n);
        }
        int count = Integer.MAX_VALUE;
        for (int i = 1; i * i < n; i++) {
            count = Math.min(count,numSquares(n - i * i) + 1);
        }
        //key为总数 count为所需要的平方数个数
        map.put(n,count);
        return count;
}

零钱兑换和完全平方数一样，只是把完全平方数换成了硬币

  
      int[] dp = new int[amount + 1];
        Arrays.fill(dp,amount + 1);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int j = 0; j < coins.length; j++) {
                if (i - coins[j] < 0) {//背包容量装不下物品
                    continue;
                }
                dp[i] = Math.min(dp[i-coins[j]] + 1,dp[i]);
            }
        }
        return dp[amount] > amount ? -1 : dp[amount]; //所给硬币不能组成指定金额
    }

3、分割等和子集
这个相当于01背包问题，物品只能取一次
状态转移方程：dp【i】【j】表示前i个物品背包容量为j，能否恰好装满这个背包，能的话dp【i】【j】为true 不能的话dp【i】【j】为false，前i个物品的取值范围为1-i
dp【i】【0】为true 背包没容量肯定能装满,dp【0】【j】为false 没有物品肯定不能装满背包
dp【0】【0】为true
状态转移：(1)不把第 i 个物品装入背包，背包容量不足就不把第 i 个物品装入背包，那么是否能够恰好装满背包，取决于上一个状态 dp【i-1】【j】，继承之前的结果， dp【i】【j】 = dp【i-1】【j】
(2)把这第 i 个物品装入了背包，那么是否能够恰好装满背包，取决于状态 dp【i-1】【j-num[i]】和dp【i-1】【j】，dp【i】【j】 = dp【i-1】【j】|| dp【i-1】【j-num[i]】

 public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        int sum1 = sum/2;
        int length = nums.length;
        boolean[][] dp = new boolean[length +1][sum+1];//dp[i][j]表示前i个物品背包容量为j，能否恰好装满这个背包 能的话dp[i][j]为true 不能的话dp[i][j]为false
        for (int i = 0; i <= length; i++)
            dp[i][0] = true;                                  //dp[i][0]为true 背包没容量肯定能装满 dp[0][j]为false 没有物品肯定不能装满背包
        for (int i = 1; i <= length; i++) {
            //不把这第 i 个物品装入背包，那么是否能够恰好装满背包，取决于上一个状态 dp[i-1][j]，继承之前的结果
            //把这第 i 个物品装入了背包，那么是否能够恰好装满背包，取决于状态 dp[i-1][j-nums[i-1]]
            for (int j = 1; j <= sum1; j++) {
                //装不下 不装
                if (j - nums[i-1] < 0) {
                    dp[i][j] = dp[i-1][j];
                //装得下 装或不装
                } else {
                    dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
                }
            }
        }
        return dp[length][sum1];
    }

4、目标和
设正数和为x，负数和为y，数组的和为sum
推导：
target = x - y, y = x - target
sum = x + y,把y = x - target代入，sum = x + x - target,2x = sum + target, x = (sum + target)/2 = s
然后问题就转化成了有多少种方案选物品使得背包容量为s
状态转移方程：dp【j】= dp【j-nums[i]】+ dp【j】，dp【j】是当前物品不装的方案数，dp【j-nums[i]】是当前物品装的方案数

 public int findTargetSumWays(int[] nums, int S) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        S = Math.abs(S);
        if (S > sum || (S + sum) % 2 != 0) {
            return 0;
        }
        int target = (S + sum) / 2;
        int[] dp = new int[target+1];
        dp[0] = 1;//背包容量为0只有一种方案就是一件物品都不装
        for (int i = 0; i < nums.length; i++) {
            for (int j = target; j >= nums[i]; j--) {//j >= num[i]的意思是背包容量要大于等于物品重量
                dp[j] = dp[j] + dp[j-nums[i]]; //dp[j]是不装，dp[j-num[i]]是装 总方案数=当前物品不装的方案数+当前物品装的方案数
            }
        }
        return dp[target];
    }

课程表
拓扑排序
BFS:
先初始化每个课程的入度，以及每个课程的后继课程
先把入度为0的课程入队，然后出队表示这个课程已经学习了，对应后继课程的入度减1，再把入度为0的课程入队，直到队列为空，最后如果还有课程的入度不为0即不能完成所有课程的学习

public boolean canFinish(int numCourses, int[][] prerequisites) {
        //课号，课号的入度
        Map<Integer, Integer> inDegree = new HashMap<>();
        //先放课程
        for (int i = 0; i < numCourses; i++) {
            inDegree.put(i,0);
        }
        //当前课程所对应的后继课程
        Map<Integer, List<Integer>> dependency = new HashMap<>();
        for (int[] relate : prerequisites) {
            //例如[3,0]，学习3之前要学习0，更新课程3的入度和课程0的依赖
            int cur = relate[1];//当前课程
            int next = relate[0];//当前课程的后继课程
            //更新入度
            inDegree.put(next, inDegree.get(next) + 1);
            //更新依赖
            if (!dependency.containsKey(cur)) {
                dependency.put(cur,new ArrayList<>());
            }
            dependency.get(cur).add(next);
        }
        //BFS，入度为0的课程加入队列，入度为0的课程是还没有修的并且没有前置课程可以进行学习的
        Queue<Integer> queue = new LinkedList();
        for (int key : inDegree.keySet()) {
            if (inDegree.get(key) == 0) {
                queue.offer(key);
            }
        }
        while (!queue.isEmpty()) {
            //出队一个节点，代表学习了这门课程，然后这门课程的后继课程的入度减一
            int poll = queue.poll();
            if (!dependency.containsKey(poll)) {
                continue;
            }
            List<Integer> successorList = dependency.get(poll);
            for (int num : successorList) {
                //入度减1
                inDegree.put(num,inDegree.get(num) - 1);
                //入度为0表示课程的前置课程已经学习完了可以开始学习了,存在环的两门课程入度不会为0，即无法进行学习
                if (inDegree.get(num) == 0) {
                    queue.offer(num);
                }
            }
        }
        for (int value : inDegree.values()) {
            if (value != 0) {
                return false;
            }
        }
        return true;
    }

最大正方形

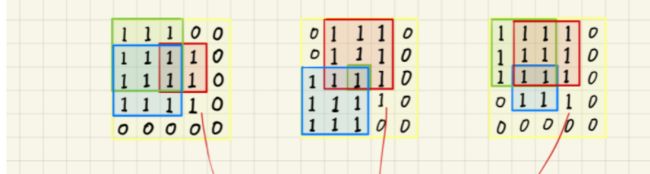
dp【i】【j】表示当前格子为正方形右下角格子所能组成的最大正方形边长
dp【i】【j】是通过上方正方形边长，左边正方形边长，左上方正方形边长，这三个取最小值加1求出来的，类似于木桶效应
图1是上方正方形边长最短，图二是左上方正方形边长最短，图三是左方正方形边长最短
dp【i】【j】= min(dp【i-1】【j】，dp【i】【j-1】，dp【i-1】【j-1】)+1

public int maximalSquare(char[][] matrix) {
           int row = matrix.length;
        if(row == 0) return 0;
        int column = matrix[0].length;
        if(column == 0) return 0;
        int[][] dp = new int[row][column];
        int res = 0;
        for (int i = 0; i < column; i++) {
            if (matrix[0][i] == '1') {
                dp[0][i] = 1;
            }
            res = Math.max(res,dp[0][i]);
        }
        for (int i = 0; i < row; i++) {
            if (matrix[i][0] == '1') {
                dp[i][0] = 1;
            }
            res = Math.max(res,dp[i][0]);
        }
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < column; j++) {
                if (matrix[i][j] == '1') {
                    int min = Math.min(dp[i - 1][j], dp[i][j - 1]);
                    dp[i][j] = Math.min(min,dp[i - 1][j - 1]) + 1;
                }
                res = Math.max(res,dp[i][j]);
            }
        }
        return res * res;

437. 路径总和 III
算出每个节点到根节点的路径和称为前缀和，然后两个节点的前缀和相减看是否等于target

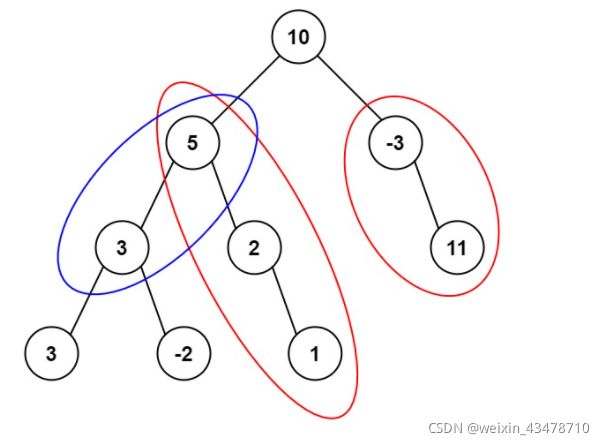
如上图，target为8，节点3的前缀和为18，节点10的前缀和为10，这两个节点的前缀和相减等于target，所以路径和为target的数量加1
要用一个map记录前缀和出现的次数：key是前缀和，value是对应的前缀和出现的次数，看是否存在另一个节点的前缀和等于当前节点的前缀和-target

    public int pathSum(TreeNode root, int targetSum) {
        //key:前缀和 value:这个前缀和出现了多少次
        Map<Integer, Integer> preSumMap = new HashMap<>();
        preSumMap.put(0,1);
        return pathSumDfs(root,preSumMap,targetSum,0);
    }


    private int pathSumDfs(TreeNode root, Map<Integer, Integer> preSumMap, int targetSum, int curPreSum) {
        if (root == null) {
            return 0;
        }
        int res = 0;
        curPreSum += root.val;//算当前节点的前缀和
        /**
         * 看根节点到当前节点中间的节点是否有节点的前缀和为curPreSum - targetSum
         */
        res += preSumMap.getOrDefault(curPreSum - targetSum,0);
        //更新前缀和
        preSumMap.put(curPreSum,preSumMap.getOrDefault(curPreSum,0) + 1);
        //进入下一层
        res += pathSumDfs(root.left,preSumMap,targetSum,curPreSum);
        res += pathSumDfs(root.right,preSumMap,targetSum,curPreSum);
        // 4.回到本层，恢复状态，去除当前节点的前缀和数量
        preSumMap.put(curPreSum, preSumMap.get(curPreSum) - 1);
        return res;
    }

最佳买卖股票时机含冷冻期
dp[i][0]是手上不持有股票并且不是因为股票卖出了才不持有股票的收益，能转移到0、1 不操作是转移到0 买入是转移到1
dp[i][1]是手上持有股票时的收益，可以转移到1、2，不操作是转移到1 卖出是转移到2
dp[i][2]是手上不持有股票是因为股票卖出了所以不持有股票的收益，可以转移到0 只能不操作转移到0

dp[0][0]为0表示第一天没有买入股票收益为0
dp[0][1]为-prices[0]表示第一天买入股票没有卖是负收益
dp[0][2]为0表示第一天买入股票又卖出收益0

 public int maxProfit(int[] prices) {
        int length = prices.length;
        if (length < 2) {
            return 0;
        }
        int[][] dp = new int[length][3];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];//负收益
        dp[0][2] = 0;//当天买了又卖
        /**
         * dp[i][0]是手上不持有股票并且不是因为股票卖出了才不持有股票的收益，能转移到0、1 不操作是转移到0 买入是转移到1
         * dp[i][1]是手上持有股票时的收益，可以转移到1、2，不操作是转移到1 卖出是转移到2
         * dp[i][2]是手上不持有股票是因为股票卖出了所以不持有股票的收益，可以转移到0 只能不操作转移到0
         */
        for (int i = 1; i < length; i++) {
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][2]);
            dp[i][1] = Math.max(dp[i-1][0]-prices[i],dp[i-1][1]);//当天买入所以收益减少要-prices[i]，昨天没卖今天才能买
            dp[i][2] = dp[i-1][1] + prices[i];//当天卖出所以收益增加要+prices[i]
        }
        return Math.max(dp[length-1][0],dp[length-1][2]);//最大收益肯定是最后一天不持股
    }

二叉树的序列化和反序列化
DFS:
反序列化使用一个队列，每次从队头出队一个构造根节点

public class Codec {
    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        StringBuffer sb = new StringBuffer();
        serializeDfs(root,sb);
        sb.deleteCharAt(sb.length() - 1);
        return sb.toString();
    }

    private void serializeDfs(TreeNode root, StringBuffer sb) {

        sb.append(root == null ? "null" : root.val);
        sb.append(",");
        if (root != null) {
            serializeDfs(root.left,sb);
            serializeDfs(root.right,sb);
        }
    }


    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] split = data.split(",");
        TreeNode node = deserializeDfs(split, 0);
        return node;
    }

    private TreeNode deserializeDfs(String[] split, int index) {
        if (split[index].equals("null")) {
            return null;
        }
        TreeNode node = new TreeNode(Integer.parseInt(split[index]));
        node.left = deserializeDfs(split,index++);
        node.right = deserializeDfs(split,index++);
        return node;
    }

和为K的子数组
和路径总和|||类似，求出当前前缀和，然后看map里是否已经存在另一个前缀和等于当前前缀和-target，是的话结果就加上另一个前缀和出现的次数
要先看map里面有没有然后再把当前前缀和更新到map里面，不能先更新，如果先更新的话当target为0时，每次都会在map里找到前缀和，先找后更新就不会出现这种情况

public int subarraySum(int[] nums, int k) {
        if (nums.length == 1 && nums[0] != k) {
            return 0;
        }
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0,1);//前缀和为0的出现了1次
        int preSum = 0;
        int count = 0;
        for (int i = 0; i < nums.length; i++) {
            preSum += nums[i];
            if (map.containsKey(preSum - k)) {
                count += map.get(preSum - k);
            }
            map.put(preSum,map.getOrDefault(preSum,0) + 1);

        }
        return count;
    }

最长递增子序列
状态转移方程：
dp[i]表示以i结尾的最长递增子序列
当前位置的最长递增子序列等于结尾比当前位置小的最长递增子序列+1
dp[i] = max(dp[i],dp[j]+1) num[i] > num[j]才能用这个状态转移方程，dp[j]取最大的

  public int lengthOfLIS(int[] nums) {
       int len = nums.length;
        if (len < 2) {
            return len;
        }
        int[] dp = new int[nums.length];
        Arrays.fill(dp,1);
        //i为右，j为左
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0 ; j <i; j++){
                //当前数字比前面以j结尾的子序列大就更新
                //例如 当前数字是 3 前面递增子序列1,3 1,4  1,3,4 1,2 当前数字3只能和1,2组成新的递增子序列
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i],dp[j] + 1);
                }
            }
        }
        for (int i = 0; i < nums.length; i++) {
            res = Math.max(res,dp[i]);
        }
        return res;
    }

寻找重复数
先找中间数，然后统计小于等于中间数的个数，如果个数等于中间数，那么重复数就在区间（mid+1,right），left=mid+1收缩左边界，否则重复数在区间（left,mid），right=mid收缩右边界，最后左边界和右边界相等时左边界或右边界就是重复的数

 public int findDuplicate(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left)/2;
            int count = 0;
            for (int num : nums) {
                if (num <= mid) {
                    count++;
                }
            }
            //小于等于mid的数正常来说是有mid个的
            if (count > mid) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

单词搜索
DFS+回溯：
矩阵的每个位置都要向上下左右进行dfs递归并且把当前位置设为已访问，并且递归之后要进行回溯把当前位置恢复为未访问
当可以遍历到字符串的最后一个字符就搜索成功
数组越界或当前位置访问过或当前位置不是字符串的字符就返回（相当于剪枝）

public boolean exist(char[][] board, String word) {
        boolean[][] visited = new boolean[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (existDfs(board,i,j,visited,word,0)) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean existDfs(char[][] board, int row, int column, boolean[][] visited, String words, int index) {
        if (row < 0 || row > board.length - 1 || column < 0 || column > board[0].length - 1
                || visited[row][column] || board[row][column] != words.charAt(index)) {
            return false;
        }
        //遍历到单词的最后一个字母
        if (index == words.length() - 1) {
            return true;
        }
        visited[row][column] = true;
        boolean down = existDfs(board,row+1,column,visited,words,index+1);//向下
        boolean up = existDfs(board,row-1,column,visited,words,index+1);//向上
        boolean left = existDfs(board,row,column+1,visited,words,index+1);//向左
        boolean right = existDfs(board,row,column-1,visited,words,index+1);//向右
        boolean res = down || up || left || right;
        visited[row][column] = false;
        return res;
    }

回文子串
方法一：动态规划
状态：dp[i][j]表示字符串（i,j）是否是回文字符串
base case: 一个字符的字符串肯定是回文字符串，即i等于j时
状态转移方程：当char[i] == char[j]时, 如果字符串长度小于等于2肯定是回文字符串dp[i][j]为true
否则dp[i][j] = dp[i+1][j-1],继承前一个状态

public int countSubstrings(String s) {
   if (s.length() < 2) {
            return 1;
        }
        int res = 0;
        int len = s.length();
        char[] chars = s.toCharArray();
        boolean[][] dp = new boolean[len][len];
        for (int j = 0; j < len; j++) {
            // i<=j是因为左边不能比右边大
            for (int i = 0; i <= j; i++) {
                if (chars[i] == chars[j]) {
                    //长度小于3肯定是回文串
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        //dp[i][j]:abba dp[i+1][j-1]:bb
                        dp[i][j] = dp[i+1][j-1]; // 这步的作用是看dp[i+1][j-1]是否为true 是的话dp[i][j]也为true
                    }
                    if (dp[i][j]) {
                        res++;
                    }
                }
            }
        }
        return res;
        }
}

方法二：中心点扩展法
找出所有的中心点然后向两边扩散，奇数回文串的中心点为1个，偶数回文串的中心点为2个，扩展之后也是回文串结果就加1

int num = 0;
    public int countSubstrings(String s) {
        for (int i=0; i < s.length(); i++){
            count(s, i, i);//回文串长度为奇数
            count(s, i, i+1);//回文串长度为偶数
        }
        return num;
    }
    
    public void count(String s, int start, int end){
        while(start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)){
            num++;
            start--;
            end++;
        }
    }

滑动窗口最大值
使用一个单调队列来记录滑动窗口的最大值
队尾入队一个，就看是否比队尾的元素大，比队尾元素大队尾元素就从队尾出队，直到加入的元素比队尾元素小，加入的元素才入队
窗口向前滑一位，就把右侧元素加入单调队列，左侧元素如果是滑动窗口最大值就从单调队列的队头出队，如果左侧元素不是滑动窗口最大值就不会在单调队列里，因为滑动窗口最大值入队之前左侧元素比滑动窗口最大值小所以会从队尾出队，滑动窗口最大值才能入队
举个例子：
[1 3 -1] -3 5 3 6 7 ，当前单调队列为3，-1，左侧元素1在3入队之前会从队尾出队，然后3才能入队 队头为3
1 [3 -1 -3] 5 3 6 7窗口向前滑一位，单调队列变成3，-1，-3 队头为3
1 3 [-1-3 5 ] 3 6 7窗口向前滑一位，单调队列变成5 队头为5
1 3 -1 [-3 5 3] 6 7窗口向前滑一位，单调队列变成5,3 队头为5
1 3 -1 -3 [ 5 3 6 ] 7窗口向前滑一位，单调队列变成6 队头为6
1 3 -1 -3 5 [ 3 6 7]窗口向前滑一位，单调队列变成7 队头为7
图片表示比较清晰
4入队把体重比它小的321都压扁了

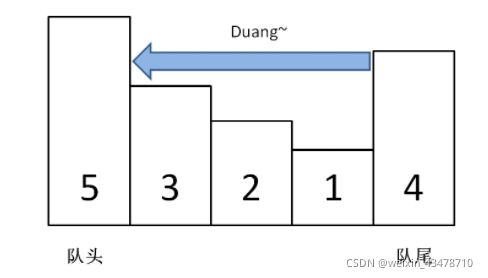
5入队把体重比它小的4321都压扁了

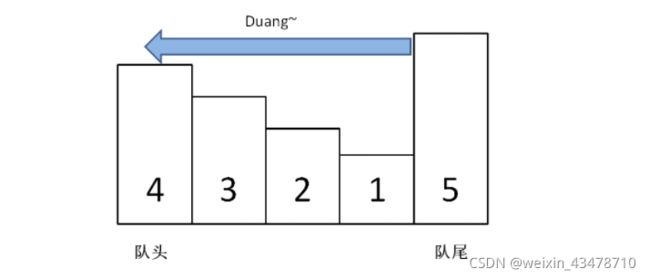
 public int[] maxSlidingWindow(int[] nums, int k) {
            Deque<Integer> queue = new LinkedList();
            //单调队列最大值为队头
            MonotonicQueue monoQueue = new MonotonicQueue();
            List<Integer> list = new ArrayList<>();
            for (int i = 0; i < nums.length; i++) {
                if (i < k - 1) {
                    while (!queue.isEmpty() && queue.getLast() < nums[i]) {
                        queue.pollLast();
                    }
                    queue.offerLast(nums[i]);
                } else {
                    //窗口向前滑加入新的数字 右侧元素
                    while (!queue.isEmpty() && queue.getLast() < nums[i]) {
                        queue.pollLast();
                    }
                    queue.offerLast(nums[i]);
                    list.add(queue.peek());//添加结果
                    //窗口向前滑左侧的数字被移除
                    if (!queue.isEmpty()) {
                        if (nums[i-k+1] == queue.peek()) {
                            queue.pollFirst();
                        }
                    }
                }
            }
            return list.stream().mapToInt(x -> x).toArray();
    }

编辑距离
删除操作：
dp[i-1][j]
doge i是4
dog j是3
doge删除一个e变成dog

插入操作：
dp[i][j-1]
dog i是3
doge j是4
dog插入一个变成e变成doge4r

t len = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len + 1][len2 + 1];
        //字符串word1为0时，每次都是插入操作
        for (int i = 1; i <= len2; i++) {
            dp[0][i] = i;
        }
        //字符串word2为0时，每次都是删除操作
        for (int i = 1; i <= len; i++) {
            dp[i][0] = i;
        }
       for (int i = 1; i <= len; i++) {
            for (int j = 1; j <= len2; j++) {
                //字符相等就什么都不做
                if (word1.charAt(i-1) == word2.charAt(j-1)) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                //不相等就取插入、删除、替换操作里的最小值
                    int min = Math.min(dp[i - 1][j], dp[i][j - 1]);//dp[i-1][j]是删除 dp[i][j - 1]是插入
                    dp[i][j] = Math.min(min,dp[i-1][j-1]) + 1;//dp[i-1][j-1]是替换
                }
            }
        }
        return dp[len][len2];
    }

打家劫舍|||
状态转移方程：
dp[i][0]表示第i个节点不偷的收益
dp[i][1]表示第i个节点偷的收益
当前节点偷，左右子节点就不能偷：
当前节点的值+左节点不偷的值+右节点不偷的值 root.val + left[0] + right[0]
当前节点不偷，左右子节点可偷可不偷：
左节点偷或不偷的最大值+右节点偷或不偷的最大值 max(left[0],left[1]) + max(right[0],right[1])

public int rob(TreeNode root) {
        int[] res = robDfs(root);
        return Math.max(res[0],res[1]);
    }

    private int[] robDfs(TreeNode root) {
        if (root == null) {
            return new int[]{0,0};
        }
        int[] left = robDfs(root.left);
        int[] right = robDfs(root.right);
        //dp[0]当前节点不偷，dp[1]当前节点偷
        int[] dp = new int[2];
        dp[0] = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);//当前节点不偷，所以左右子节点可以偷可以不偷
        dp[1] = root.val + left[0] + right[0]; //当前节点偷，所以左右子节点都不能偷
        return dp;
    }

戳气球
状态转移方程：
dp[i][j] = dp[i][k] + dp[k][j] + point[i]*point[j]*point[k]
i和j是开区间，要先算出戳破i到k之间和k到j之间的气球最大得分然后再加上戳破k气球的得分就是戳i到j之间的气球的最大得分

 public int maxCoins(int[] nums) {
         int length = nums.length;
        //左右两侧的虚拟气球
        int[] points = new int[length + 2];
        points[0] = points[length + 1] = 1;
        //初始化气球分数
        for (int i = 1 ; i <= length; i++) {
            points[i] = nums[i-1];
        }
        //i要比j小2中间才有气球戳 两个气球相邻中间没气球戳
        int[][] dp = new int[length + 2][length + 2];
        //i从最后一个气球开始,一直遍历到第一个气球
        for (int i = length; i >= 0; i--) {
            //j从i的右一个气球开始，遍历到最后一个气球
            for (int j = i + 1; j < length + 2; j++) {
                //最后戳破的气球从i的右一个开始选，选到j的左边一个
                for (int k = i + 1; k < j; k++) {
                    dp[i][j] = Math.max(dp[i][j],dp[i][k] + dp[k][j] + points[i] * points[k] * points[j]);
                }
            }
        }
        return dp[0][length+1];//dp[0][length+1]表示戳破第一个气球到最后一个气球之间的气球的最大得分
    }

找到字符串中所有字母异位词
用一个map需要的字符出现的次数，例如字符串abc，a的出现次数为1，b的出现次数为1,c的出现次数为1
当滑动窗口最右侧字符在window的出现次数比need多就移动左指针直到右侧字符window的出现次数等于need里的
cbaebabacd
right = 0,c的出现次数为1
right = 1,b的出现次数为1
right = 2,a的出现次数为1,left = 0,此时窗口大小刚好等于字符串abc的大小，就添加一个结果
right = 3,e的出现次数为1，字符串abc里e的出现次数为0，e出现次数比abc的大，就收缩窗口直到e的出现次数为0，left=1，c的出现次数为0,left=2，b的出现次数为0,left=3,a的出现次数为0,left=4,e的出现次数为0
继续扩大窗口rright = 4,b的出现次数为1
right = 5,a的出现出现次数为1
right = 6,b的出现次数为2，字符串abc里b的出现次数为1,b出现次数比abc的大，就收缩窗口直到b的出现次数为1,left = 5,b的出现次数为1
继续扩大窗口，right = 7，a的出现次数为2,字符串abc里a的出现次数为1，a出现次数比abc的大，就收缩窗口直到a的出现次数为1,left = 6,a的出现次数为1
继续扩大窗口，right = 8,c的出现次数为1，此时窗口大小刚好等于字符串abc的大小，就添加一个结果
right = 9,d的出现次数为1，字符串abc里d的出现次数为0，d出现次数比abc的大，就收缩窗口直到d的出现次数为0，left = 7，b的出现次数为0，left = 8,a的出现次数为0，left = 9，c的出现次数为0，left = 10,d的出现次数为0
right = 10，此时遍历完字符串cbaebabacd退出循环

public List<Integer> findAnagrams(String s, String p) {
        int[] need = new int[26];
        int[] window = new int[26];
        char[] sChars = s.toCharArray();
        char[] pChars = p.toCharArray();
        //统计出现次数
        for (int i = 0; i < p.length(); i++) {
            need[pChars[i] - 'a'] += 1;
        }
        int left = 0,right = 0;
        List<Integer> res = new ArrayList<>();
        while (right < s.length()) {
            int rightChar = s.charAt(right) - 'a';    
            window[rightChar] += 1;
            //当滑动窗口最右侧字符在window的出现次数比need多就收缩窗口直到右侧字符在window的出现次数等于need里的
            while (window[rightChar] > need[rightChar]) {
                int leftChar = s.charAt(left) - 'a';
                left++;
                window[leftChar] -= 1;//窗口收缩
            }
            if (right - left + 1 == p.length()) {
                res.add(left);
            }
            right++;//扩大窗口
        }
        return res;
    }

最短无序连续子数组
从左往右遍历，记录最大值，然后如果当前值比最大值小，证明最大值到当前值这段不是升序的，需要进行排序，然后最后一个比最大值小的就是要排序段的右区间
例如 1 3 5 2 当前值2比最大值小，即5到2这段不是升序的需要进行排序
从右往左遍历，记录最小值，然后如果当前值比最大值大，证明当前值到最小值这段不是升序的，需要进行排序，然后最后一个比最小值大的就是要排序段的右区间
例如 1 2 3 5 4 当前值5比最小值4大，即5到4这段不是升序的需要进行排序

 public int findUnsortedSubarray(int[] nums) {
        int len = nums.length;
        int min = nums[len-1];//初始化最后一个数为最小值
        int max = nums[0];//初始化第一个数为最大值
        int begin = 0, end = -1;
        //左边界是从右往左找的最后一个大于最小值的数 右边界是从左往右找的最后一个小于最大值的数
        for (int i = 0; i < len; i++) {
            //从左往右遍历，如果最大值大于当前数，证明最大数和当前值之间不符合升序排序，然后更新右边界为当前数
            if (nums[i] < max) {
                end = i;
            } else {
                //否则更新当前值为最大值
                max = nums[i];
            }
            //从右往左遍历，如果最小值大于当前数，证明当前数和最小数之间不符合升序排序，然后更新左边界为当前数
            if (nums[len - i - 1] > min) {
                begin = len - i - 1;
            } else {
                //否则更新当前值为最小值
                min = nums[len - i - 1];
            }
        }
        return end - begin + 1;
    }

根据身高重建队列

public int[][] reconstructQueue(int[][] people) {
        Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]);

        LinkedList<int[]> list = new LinkedList<>();
        for (int[] i : people) {
            list.add(i[1], i);
        }

        return list.toArray(new int[list.size()][2]);
    }

最小覆盖子串

首先记录目标字符有哪些，字符串t的目标字符有A、B、C
扩大窗口，先找到可行解——纳入了所有目标字符,
此时停止扩大窗口，开始收缩窗口，优化可行解为可能的最优解，有目标字符丢失就为可能的最优解然后就不再收缩窗口

例如可行解为ADOBEC,此时再收缩就丢失目标字符A，所以此时ADOBEC刚好为可能的最优解，然后收缩窗口变成DOBEC，此时丢失了目标字符A,再扩大窗口补充目标字符A

例如可行解为DOBECODEBA,当收缩窗口至CODEBA时，再收缩就丢失目标字符C，所以此时CODEBA为可能的最优解，然后收缩窗口变成ODEBA，此时丢失了目标字符C,再扩大窗口补充目标字符C

可行解为ODEBANC,当窗口收缩至BANC时，再收缩就丢失目标字符B，所以此时BANC为可能的最优解，然后收缩窗口变成ANC，此时丢失了目标字符B,再扩大窗口补充目标字符B,不过此时窗口已经来到了字符串s的末尾，不能扩大了

public String minWindow(String a, String b) {
        char[] aChars = a.toCharArray();
        int[] need = new int[128];
        for (int i = 0; i < b.length(); i++) {
            need[b.charAt(i)] += 1;
        }
        int left = 0, right = 0, count = b.length(), windowSize = Integer.MAX_VALUE, start = 0;
        while (right < a.length()) {
            char rightChar = aChars[right];
            //如果当前字符是需要的，即存在在字符串b的
            if (need[rightChar] > 0) {
                count--;//找到一个字符所有需要的字符数减1
            }
            need[rightChar]--;
            //窗口已经包含所有需要的字符，就可以收缩窗口然后更新结果
            if (count == 0) {
                //收缩窗口直到遇到第一个需要的字符，因为小于都是多余的字符 等于0的才是需要的字符
                while (left < right && need[aChars[left]] < 0) {
                    need[aChars[left]]++;//多余字符需要次数加1
                    left++;//收缩窗口
                }
                System.out.println(a.substring(left,right+1));
                //当前窗口更小
                if (right - left + 1 < windowSize) {
                    windowSize = right - left + 1;
                    start = left;
                }
                //查找下一个包含所有需要字符的窗口
                //把需要的字符移除找下一个窗口 例如当前窗口是 ADOBEC 去除需要的字符A need[A]从0变成1
                // 变成 DOBEC然后扩大窗口找下一个包含所有需要字符的窗口
                need[aChars[left]]++;//+1相当于找下一个窗口哪里出现了这个字符
                left++;//
                count++;
            }
            right++;//扩大窗口
        }
        return windowSize == Integer.MAX_VALUE ? "" : a.substring(start,start + windowSize);
    }

柱状图中最大的矩形
使用单调栈，如果当前元素比栈顶元素小，栈顶元素就出栈，直到当前元素比栈顶元素大
然后以栈顶元素为矩阵的最大面积是栈顶元素长度*（当前元素索引-栈顶元素的下一个的索引-1）
例如柱形图2 1 5 6 2 3 栈顶元素是5，栈顶元素的下一个是1，,对应索引是1， 当前元素是2，对应索引是4,
所以以栈顶元素为矩阵的最大面积是5 x (4 - 1 - 1) = 10
还要在最左侧和最右侧弄两个高度为0的虚拟柱体处理边界问题，不加的话2为栈顶元素时没有栈顶元素的下一个元素

public int largestRectangleArea(int[] heights) {
        int[] tmp = new int[heights.length + 2];
        System.arraycopy(heights,0,tmp,1,heights.length);
        //单调递减栈 存的是索引
        Deque<Integer> stack = new LinkedList<>();
        int area = 0;
        for (int i = 0; i < tmp.length; i++) {
            //对于每个栈顶柱体，左侧比他小的柱体就是栈顶下面的柱体,当前柱体高度比栈顶柱体高度小，即当前柱体是比栈顶柱体高度小的右侧柱体
            //找到左侧和右侧小的柱体就可以计算面积,面积是不包括左侧小的柱体和右侧小的柱体
            // 例如5左侧小的柱体是1 右侧小的柱体是2  2 1 5 6 2 3 5的最大面积是5 6 不包括 1 2
            while (!stack.isEmpty() && tmp[stack.peek()] > tmp[i]) { //栈顶柱体比当前柱体大就出栈因为要保证单调性
                int top = tmp[stack.pop()];//高度
                //i是比栈顶柱体右侧小的柱体，stack.peek()是比栈顶柱体左侧小的柱体
                area = Math.max(area,(i - stack.peek() - 1) * top);
            }
            //直到栈顶柱体比当前柱体小当前柱体才入栈
            stack.push(i);
        }
        return area;
    }

把二叉搜索树转换为累加树
使用中序遍历，已经计算的总和+当前节点的值，然后作为当前节点的值

int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if (root == null) {
            return null;
        }
        convertBST(root.right);
        sum += root.val;
        root.val = sum;
        convertBST(root.left);
        return root;
    }

最大矩形
把二维矩阵转换成一维的柱形图，然后算柱状图中最大的矩形

public int maximalRectangle(char[][] matrix) {
        int[] heights = new int[matrix[0].length];
        int res = 0;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                //当前列高度加1
                if (matrix[i][j] == '1') {
                    heights[j] += 1;
                } else {
                    heights[j] = 0;
                }
            }
            res = Math.max(res,largestRectangleArea(heights));
        }
        return res;
    }

public int largestRectangleArea(int[] heights) {
        int[] tmp = new int[heights.length + 2];
        System.arraycopy(heights,0,tmp,1,heights.length);
        //单调递减栈 存的是索引
        Deque<Integer> stack = new LinkedList<>();
        int area = 0;
        for (int i = 0; i < tmp.length; i++) {
            //对于每个栈顶柱体，左侧比他小的柱体就是栈顶下面的柱体,当前柱体高度比栈顶柱体高度小，即当前柱体是比栈顶柱体高度小的右侧柱体
            //找到左侧和右侧小的柱体就可以计算面积,面积是不包括左侧小的柱体和右侧小的柱体
            // 例如5左侧小的柱体是1 右侧小的柱体是2  2 1 5 6 2 3 5的最大面积是5 6 不包括 1 2
            while (!stack.isEmpty() && tmp[stack.peek()] > tmp[i]) { //栈顶柱体比当前柱体大就出栈因为要保证单调性
                int top = tmp[stack.pop()];//高度
                //i是比栈顶柱体右侧小的柱体，stack.peek()是比栈顶柱体左侧小的柱体
                area = Math.max(area,(i - stack.peek() - 1) * top);
            }
            //直到栈顶柱体比当前柱体小当前柱体才入栈
            stack.push(i);
        }
        return area;
    }

合并K个有序链表
类似于归并排序，自底向上，当链表被分成一个节点时就开始合并

 public ListNode mergeKLists(ListNode[] lists) {
        return mergeKListsDfs(lists,0,lists.length-1);
    }

    private ListNode mergeKListsDfs(ListNode[] lists, int left, int right) {
        //只剩一个链表
        if (left == right) {
            return lists[left];
        }
        if (left > right) {
            return null;
        }
        int mid = (left + right) >> 1;
        ListNode leftNode = mergeKListsDfs(lists, left, mid);
        ListNode rightNode = mergeKListsDfs(lists, mid + 1, right);
        return mergeTwoList(leftNode,rightNode);
    }

    private ListNode mergeTwoList(ListNode a, ListNode b) {
        //其中一个为空就返回另一个
        if (a == null || b == null) {
           return a == null ? b : a;
        }

        ListNode dummy = new ListNode();
        ListNode cur = dummy;

        while (a != null && b != null) {
            if (a.val < b.val) {
                cur.next = a;
                a = a.next;
            } else {
                cur.next = b;
                b = b.next;
            }
            cur = cur.next;
        }
        cur.next = a == null ? b : a;
        a = dummy.next;
        return a;
    }

旋转链表
先断链，后拼接
链表常用技巧就是一个拿来跑，一个拿来返回结果

public ListNode rotateRight(ListNode head, int k) {
        int length = 0;
        ListNode temp = head;
        //统计长度
        while (temp != null) {
            length++;
            temp = temp.next;
        }
        //算出步长
        int remove = length - (k % length);
        if (length == 0 || length == 1 || k == 0 || remove == length) {
            return head;
        }
        ListNode cut = head;
        //算出断链位置 1->2->3->4 k = 2 就在2这里断链 变成 1->2 3->4
        for (int i = 1; i < remove; i++) {
            cut = cut.next;
        }
        ListNode next = cut.next; //3->4
        ListNode tail = next; //跑的节点
        ListNode first = next; //返回的结果
        cut.next = null;
        while (next.next != null) {
            first.next = next.next;
            next = next.next;
            tail = next;
        }
        tail.next = head;
        return first;
    }

另一种方法就是先成环，后断链