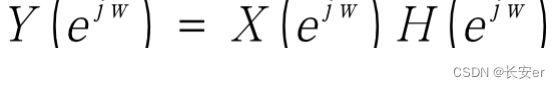数字信号处理实验：IIR数字滤波器设计及软件实现

目录

一、实验目的

二、实验原理

三、实验设备

四、实验内容及步骤

五、实验结果及分析

六、实验主程序框图及程序清单

七、实验总结

---

一、实验目的

1. 熟悉用双线性变换法设计IIR数字滤波器的原理与方法；
2. 学会调用MATLAB信号处理工具箱中滤波器设计函数（或滤波器设计分析工具FDATool）设计各种IIR数字滤波器，学会根据滤波需求确定滤波器指标参数。
3. 掌握IIR数字滤波器的MATLAB实现方法。
4. 通过观察滤波器输入、输出信号的时域波形及其频谱，建立数字滤波的概念

二、实验原理

数字滤波器是对数字信号实现滤波的线性时不变系统。数字滤波实质上是一种运算过程，实现对信号的运算处理。输入数字信号（数字序列）通过特定的运算转变为输出的数字序列，因此，数字滤波器本质上是一个完成特定运算的数字计算过程，也可以理解为是一台计算机。描述离散系统输出与输入关系的卷积和差分方程只是给数字信号滤波器提供运算规则，使其按照这个规则完成对输入数据的处理。时域离散系统的频域特性:​​​​​​​​​​​​​​

其中、分别是数字滤波器的输出序列和输入序列的频域特性（或称为频谱特性），是数字滤波器的单位取样响应的频谱，又称为数字滤经过滤波后的频域响应。只要按照输入信号频谱的特点和处理信号的目的，适当选择，使得滤波后满足设计的要求，这就是数字滤波器的滤波原理。

设计IIR数字滤波器一般采用间接法（脉冲响应不变法和双线性变换法），应用最广泛的是双线性变换法。基本设计过程是：① 将给定的数字滤波器的指标转换成过渡模拟滤波器的指标；② 设计过渡模拟滤波器；③ 将过渡模拟滤波器系统函数转换成数字滤波器的系统函数。MATLAB信号处理工具箱中的各种IIR数字滤波器设计函数都是采用双线性变换法。第6章介绍的滤波器设计函数butter、cheby1 、cheby2 和ellip可以分别被调用来直接设计巴特沃斯、切比雪夫1、切比雪夫2以及椭圆模拟与数字滤波器。本实验要求读者调用如上函数直接设计IIR数字滤波器。

本实验的数字滤波器的MATLAB实现是指调用MATLAB信号处理工具箱函数 filter对给定的输入信号x(n)进行滤波，得到滤波后的输出信号y(n）。

三、实验设备

计算机  Matlab软件

四、实验内容及步骤

1. 调用信号产生函数mstg产生由三路抑制载波调幅信号相加构成的复合信号st，该函数还会自动绘图显示st的时域波形和幅频特性曲线，如图2.1所示。由图可见，三路信号时域混叠无法在时域分离。但频域是分离的，所以可以通过滤波器的方法在频域分离，这就是本实验的目的。

2.要求将st中三路调幅信号分离，通过观察st的幅频特性曲线，分别确定可以分离st中三路抑制载波单频调幅信号的三个滤波器（低通滤波器、带通滤波器、高通滤波器）的通带截止频率和阻带截止频率。要求滤波器的通带最大衰减为0.1dB, 阻带最小衰减为60 dB。

3.编程序调用MATLAB滤波器设计函数ellipord和ellip分别设计这三个椭圆滤波器，并绘图显示其损耗函数曲线。 

4.调用滤波器实现函数filter，用三个滤波器分别对信号产生函数mstg产生的信号st进行滤波，分离出st中的三路不同载波频率的调幅信号y1(n)、y2(n)和y3(n)， 并绘图显示y1(n)、y2(n)和y3(n)的时域波形，观察分离效果。

五、实验结果及分析

1.调用信号产生函数mstg产生由三路抑制载波调幅信号相加构成的复合信号st，该函数还会自动绘图显示st的时域波形和幅频特性曲线，如图2.1所示。由图可见，三路信号时域混叠无法在时域分离。但频域是分离的，所以可以通过滤波器的方法在频域分离，这就是本实验的目的。

（1）程序运行所得波形（代码见程序清单）

​​​​​​​​​​​​​​

（2）结果分析

这个函数生成了三路调幅信号并将它们相加，最后将产生的混合信号在时域和频域上绘制出图像。

在本函数中，采样频率为10kHz，产生三路调幅信号的载波频率分别为1000Hz、500Hz、250Hz，而调制信号频率则分别为100Hz、50Hz、25Hz。产生的三路信号分别通过正弦波和载波信号相乘的方式得到，且三路信号的调幅方案均为幅度调制。

绘图部分将产生的混合信号在时域和频域上直观地展现出来。其中，时域波形显示在第一个子图中，横轴为时间，纵轴为信号幅度，此处限定了横轴范围仅为采样时间的1/8，使得波形更加清晰。第二个子图中呈现了混合信号的幅频特性，即频谱图，其中横轴为频率，纵轴为信号的幅度，由于幅度峰值可能大于1，因此在绘图前将幅度归一化到最大值为1。

通过对程序的分析，我们可以看到该程序以MATLAB语言实现了生成并展示三路调幅信号的功能，方便用户对其进行研究和分析。

2.滤波器的设计：

要求将st中三路调幅信号分离，通过观察st的幅频特性曲线，分别确定可以分离st中三路抑制载波单频调幅信号的三个滤波器（低通滤波器、带通滤波器、高通滤波器）的通带截止频率和阻带截止频率。要求滤波器的通带最大衰减为0.1dB, 阻带最小衰减为60 dB。

编程序调用MATLAB滤波器设计函数ellipord和ellip分别设计这三个椭圆滤波器，并绘图显示其损耗函数曲线。 

（1）首先讨论对于滤波器参数选取，由1可知，三路调幅信号的载波频率分别为250Hz，500Hz，1000Hz。带宽为50Hz，100Hz，200Hz。所以分离混合信号st中三路抑制载波单频调幅信号的三个滤波器（低通滤波器、带通滤波器、高通滤波器）的指标参数选取如下：

对载波频率为250Hz的调幅信号，用低通滤波器分离，其通带截止频率fp=280Hz，通带最大衰减ap=0.1dB，阻带截止频率为fs=450Hz，阻带最小衰减as=60dB。对载波频率为500Hz的调幅信号，用低通滤波器分离，其通带截止频率fpl=440Hz、fph=560Hz，通带最大衰减ap=0.1dB，阻带截止频率为fsl=275Hz、fsh=900Hz阻带最小衰减as=60dB。对载波频率为1000Hz的调幅信号，用低通滤波器分离，其通带截止频率fp=890Hz，通带最大衰减ap=0.1dB，阻带截止频率为fs=600Hz，阻带最小衰减as=60dB。

（2）程序运行波形

I 低通椭圆滤波器耗损函数曲线

II 带通椭圆滤波器耗损函数曲线

 III 高通椭圆滤波器耗损函数曲线

（2）结果分析

这段程序，通过调用函数mstg生成由三路抑制载波调幅信号相加构成的复合信号s，并对该信号进行椭圆滤波器的低通、带通、高通滤波、绘制出时域图和频谱图。

具体步骤如下：

调用mstg()函数生成长度为1600的由三路抑制载波调幅信号相加构成的复合信号s；

设置采样频率Fs=10000，采样间隔T=1/Fs;

分别设置低通、带通、高通滤波器的通、阻带边界频率；

该代码主要的功能之一是对由三路抑制载波调幅信号相加构成的混合信号进行滤波处理，得到低通、带通、高通三种处理后的信号。在处理过程中，使用了椭圆滤波器设计算法，并结合MATLAB中的相关函数实现。最后，通过绘制时域和频域波形图，直观地展示了滤波前后的信号变化。

3.调用滤波器实现函数filter，用三个滤波器分别对信号产生函数mstg产生的信号st进行滤波，分离出st中的三路不同载波频率的调幅信号y1(n)、y2(n)和y3(n)， 并绘图显示y1(n)、y2(n)和y3(n)的时域波形，观察分离效果。

（1）代码见程序清单

具体的函数调用代码

1. fp=280; fs=450;wp=2*fp/Fs;ws=2*fs/Fs; %低通
2. name='y_1(t)';LHL_filter(wp,ws,name,st,T,'low');
3. fp_L=440; fp_R=560;fs_L=275; fs_R=900;%带通
4. wp=[2*fp_L/Fs,2*fp_R/Fs];ws=[2*fs_L/Fs,2*fs_R/Fs];
5. name='y_2(t)'; LHL_filter(wp,ws,name,st,T,'bandpass');
6. fp=890; fs=600;wp=2*fp/Fs;ws=2*fs/Fs; %高通
7. name='y_3(t)';LHL_filter(wp,ws,name,st,T,'high');

（2）所得波形

I 低通y1(n)时域波形

II 带通y2(n)时域波形

III 高通信号y3(n)时域波形

（3）结果分析

在上面的代码中，已经使用椭圆滤波器对信号进行了低通、带通、高通三种不同性质的滤波，并得到了滤波后的三个不同信号y1(t)、y2(t)和y3(t)。

根据滤波后的结果和时域波形图，我们可以看出：

低通滤波器提取的是载波频率最低的调幅信号，所以y1(t)中的调幅信号频率最低；

带通滤波器提取的是载波频率在中间范围内的调幅信号，所以y2(t)中的调幅信号频率居于中间；

高通滤波器提取的是载波频率最高的调幅信号，所以y3(t)中的调幅信号频率最高。

因此，通过这些滤波器的组合，我们可以有效地将复合信号分离出三路不同频率的调幅信号。

六、实验主程序框图及程序清单

1.实验主程序框图

2. 程序清单

（代码进行了高亮处理）

（1）程序一：产生mstg信号

首先新建mstg.m文件，在该脚本文件中运行function st=mstg

1.  function st=mstg
   %产生信号st，并显示st的时域波形和频谱
   %st=mstg返回混合信号，长度N=1600
   N=1600  %长度
   Fs=10000;T=1/Fs;Tp=N*T;   %采样频率Fs=10KHz,Tp为采样时间
   t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;
   fc1=Fs/10;     %第1路调幅信号的载波频率fc1=1000Hz?
   fm1=fc1/10;    %第1路调幅信号的调制信号频率fm1=100Hz
   fc2=Fs/20;     %第2路调幅信号的载波频率fc2=500Hz??
   fm2=fc2/10;    %第2路调幅信号的调制信号频率fm2=50Hz
   fc3=Fs/40;     %第3路调幅信号的载波频率fc3=250Hz?
   fm3=fc3/10;    %第3路调幅信号的调制信号频率fm3=25Hz
   xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);%产生第1路调幅信号?
   xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);%产生第2路调幅信号
   xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);%产生第3路调幅信号???
   st=xt1+xt2+xt3;%三路调幅信号相加
   fxt=fft(st,N);     %计算信号st的频谱
   %===============绘图部分============
   subplot(3,1,1)
   plot(t,st);grid;xlabel('t/s');ylabel('s(t)');
   axis([0,Tp/8,min(st),max(st)]);title('(a)s(t)的波形')
   subplot(3,1,2)
   stem(f,abs(fxt)/max(abs(fxt)),'.');grid,title('(b) s(t)的频谱');
   axis([0,Fs/5,0,1.2]);
   xlabel('f/Hz');ylabel('幅度')
   

（2）程序二:低通滤波器

1.  function st=mstg
   %产生信号st，并显示st的时域波形和频谱
   %st=mstg返回混合信号，长度N=1600
   N=1600  %长度
   Fs=10000;T=1/Fs;Tp=N*T;   %采样频率Fs=10KHz,Tp为采样时间
   t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;
   fc1=Fs/10;     %第1路调幅信号的载波频率fc1=1000Hz?
   fm1=fc1/10;    %第1路调幅信号的调制信号频率fm1=100Hz
   fc2=Fs/20;     %第2路调幅信号的载波频率fc2=500Hz??
   fm2=fc2/10;    %第2路调幅信号的调制信号频率fm2=50Hz
   fc3=Fs/40;     %第3路调幅信号的载波频率fc3=250Hz?
   fm3=fc3/10;    %第3路调幅信号的调制信号频率fm3=25Hz
   xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);%产生第1路调幅信号?
   xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);%产生第2路调幅信号
   xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);%产生第3路调幅信号???
   st=xt1+xt2+xt3;%三路调幅信号相加
   fxt=fft(st,N);     %计算信号st的频谱
   %===============绘图部分============
   subplot(3,1,1)
   plot(t,st);grid;xlabel('t/s');ylabel('s(t)');
   axis([0,Tp/8,min(st),max(st)]);title('(a)s(t)的波形')
   subplot(3,1,2)
   stem(f,abs(fxt)/max(abs(fxt)),'.');grid,title('(b) s(t)的频谱');
   axis([0,Fs/5,0,1.2]);
   xlabel('f/Hz');ylabel('幅度')

（3）程序三:带通滤波器

Fs=10000;T=1/Fs;%采样频率Fs=10KHz,Tp为采样时间
fpl=440;fpu=560;fsl=275;fsu=900;rp=0.1;rs=60;
wp=[2*fpl/Fs,2*fpu/Fs];ws=[2*fsl/Fs,2*fsu/Fs];
[N,wp]=ellipord(wp,ws,rp,rs);
[B,A]=ellip(N,rp,rs,wp);
y2t=filter(B,A,st);
 
figure(4);
[H,w]=freqz(B,A,1000);%[h，w] = freqz（b，a，n）返回数字滤波器的n点频率响应矢量h和相应的角频率矢量w，其中分子和分母多项式系数分别存储在b和a中。
m=abs(H);
plot(w/pi,20*log(m/max(m)));
grid on;title('带通滤波损耗函数曲线');
xlabel('w/pi');ylabel('幅度'); 
figure(5);
t=0:T:(length(y2t)-1)*T;
plot(t,y2t);

（4）程序三:高通滤波器

 Fs=10000;T=1/Fs;%采样频率Fs=10KHz,Tp为采样时间
fp=890;fs=600;Rp=0.1;As=60;%设置参数
wp=2*fp/Fs;ws=2*fs/Fs;%WP，WS是通带截止频率，阻带截止频率的归一化值
[N,wpo]=ellipord(wp,ws,Rp,As,'s')
[B,A]=ellip(N,Rp,As,wpo,'high');
y3t=filter(B,A,st);
 
%=========绘图=============
figure(6);
[H,W]=freqz(B,A,1000);%[h，w] = freqz（b，a，n）返回数字滤波器的n点频率响应矢量h和相应的角频率矢量w，其中分子和分母多项式系数分别存储在b和a中。
m=abs(H);
plot(W/pi,20*log(m/max(m)));grid on;title('高通滤波损耗函数曲线');
xlabel('w/pi');
ylabel('幅度');
% axis([0,1,0,1.2*max(H)])
% % yt='y3(t)';
figure(7);
plot(t,y3t);title('高通滤波后的波形');
xlabel('t/s');ylabel(y3(t));

七、实验总结

本实验通过调用MATLAB信号处理工具箱中的滤波器设计函数和滤波器实现函数，学习了IIR数字滤波器的设计和实现方法。具体实验步骤包括：生成由三路抑制载波调幅信号相加构成的混合信号，观察其时域和频域波形，并通过椭圆滤波器的低通、带通、高通滤波处理分离出混合信号中的三路单频调幅信号；调用MATLAB的滤波器设计函数ellipord和ellip进行椭圆滤波器的设计，并绘制损耗函数曲线；调用滤波器实现函数filter对混合信号进行滤波，分离出三路单频调幅信号，并绘制其时域波形。

通过利用Matlab对混合信号st的生成、对椭圆滤波器的低通、带通、高通滤波进行处理分离，让我对Matlab的使用更加熟悉，能更加熟练的调用Matlab的内置函数进行滤波器的代码编写。整个编程的过程也让我更深入的理解了滤波器的实现原理，通过生成波形也让旅滤波的过程生动形象的呈现出来。

通过本次实验，我学习了双线性变换法设计IIR数字滤波器的原理和方法，掌握了MATLAB信号处理工具箱中各种IIR数字滤波器设计函数的使用方式和参数设置方法，深入理解了椭圆滤波器的性质和特点。同时，我也感受到在数字信号处理中滤波器的重要性，滤波器能够有效地去除信号中的噪声和干扰，提高信号的质量和可靠性。