【论文解读】NeurIPS 2021| 基于置信度校正可信图神经网络
题目: 基于置信度校正可信图神经网络
会议: NeurIPS 2021
论文地址:https://arxiv.org/abs/2109.14285
自信点,我的GNN们
图神经网络 (GNN) 卓越的性能已经广受关注,但其预测结果是否值得信赖却有待探索。之前的研究结果表明,许多现代神经网络对其预测具有过度自信的现象。然而与之不同的是,我们发现 GNN对其预测结果却呈现出欠自信的现象。因此,要想获得一个可信的GNN,亟需对其置信度进行校正。在本文中,我们设计了一种拓扑感知的后处理校正函数,并由此提出了一种新颖的可信赖 GNN 模型。具体来说,我们首先验证了图中的置信度分布具有同质性的特点,由此启发我们再次利用GNN模型来为分类GNN模型学习校正函数(CaGCN)的想法。CaGCN 能够为每个节点学习到一种从分类 GNN 的输出到校正后的置信度的唯一转换,同时这种转换还能够保留类间的序关系,从而满足保存精度的属性。此外,我们还将CaGCN应用于自训练框架,结果表明可以通过对置信度进行校正获得更可信的伪标签,从而并进一步提高性能。我们通过大量实验证明了我们提出的模型在置信度校正方面和在提高分类准确率方面的有效性。
总结(2-1-1):
2种现象:GNN的预测结果具有欠自信现象;好的置信度分布具有同质性现象;
1个模型:CaGCN
1类应用:置信度调整后的GNN可以有效应用于自训练框架
1 引言
图数据在现实世界中是无处不在的,而图神经网络(GNNs)已经在多种图(graph)数据相关的任务中拥有了卓越的性能。然而在许多现实世界的应用中,高预测准确率并不是我们唯一的追求。例如在许多安全相关的应用中,更渴望获得一个可信的模型。这里的可信指得是模型对预测的置信度可以真实地反映出模型预测的准确率。如果这两者相等,我们称其是校正的,这代表模型是可信的。事实上,深度学习中模型的校正能力早已经在如计算机视觉、自然语言处理等多个领域内被探索过,其结论是现代神经网络大多数是没有被校正的,并且对其预测是过于自信的。然而,还并没有人探究过图领域中模型的校正能力。所以,现有的图神经网络模型的校正能力到底如何呢,模型是否也对其预测过于自信呢?
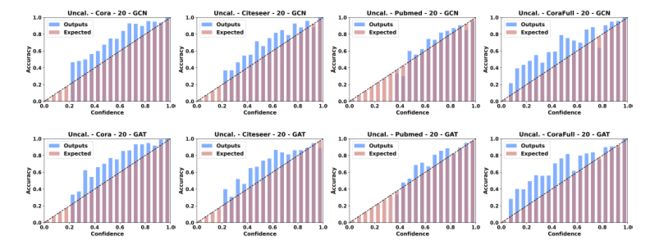
带着这个问题,我们对节点分类任务中模型的校正能力进行了实验探究。实验结果如图1所示,其中横坐标代表模型(GCN或者GAT)预测的置信度,取值范围为[0,1],我们将其划分为20等份,纵坐标代表相应置信度区间的平均分类准确率。一般来说,如果模型已经被完美的校正,其置信度应该近似等于该区间的平均分类准确率,换句话说,图1中的蓝色柱(实际输出)应与红色柱(期望输出)对齐。但是我们发现,实际上在大部分情况下,蓝色柱高于红色柱,这说明模型的分类准确率高于其置信度,模型对其预测是不自信的。这与其他领域中的结论正好相反。
图1 GCN和GAT在Cora、Citeseer、Pubmed、CoraFull数据集上的可靠性直方图。
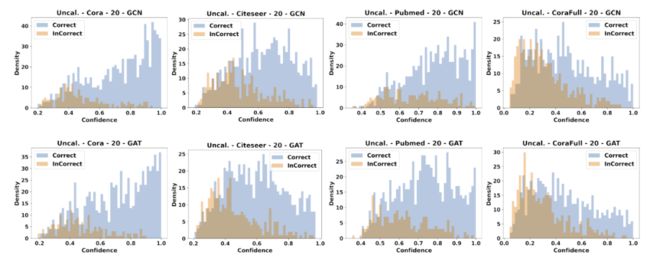
此外,我们可视化了节点的置信度分布,如图2所示,其中横坐标代表置信度,纵坐标代表对该置信度下节点数量的密度估计。从图2中我们可以明显观察到,许多预测正确(蓝色)节点的置信度分布在低置信度区间中。这可以部分解释我们上面结论,即图模型是不自信的。
图2 GCN和GAT在Cora、Citeseer、Pubmed、CoraFull数据集上的置信度分布
接下来,我们将提出图领域中置信度的校正方法——CaGCN。
2 方法
给定一个graph 的邻接矩阵 和其特征矩阵 ,对于一个层GCN来说,其输出可以通过如下方法得到:
其中 代表GCN的第层的权重,代表激活函数。接下来我们设计的置信度校正函数应该满足如下三个属性:(1)考虑网络拓扑 (2)是一个非线性函数 (3)能保存分类GCN的分类精度。
基于GCN设计的校正函数
我们假设在一个graph中,节点置信度的ground-truth分布应该满足同配(homophily)属性。我们首先设计实验验证了这一点,即利用一个经典的校正函数 tenperature scaling (TS) 对分类模型GCN的每个节点的置信度进行校正,然后计算这些节点置信度的总变差,结果如图3所示。显然,相比于没有校正(Uncal.)的情况,校正后的置信度的总变差有了明显的下降,这证明了我们假设的正确性。考虑到GCN天然可应用于高同配性图,具有平滑邻居节点信号的能力,我们利用另一个GCN作为我们的校正函数,我们称其为CaGCN。
图3 graph中置信度的同配性验证实验具体来说,CaGCN以分类GCN的输出作为输入,输出校正后的每一个节点的置信度,如下所示:
其中是softmax算子。可以看到,CaGCN能够学习到一种非线性变换,并且将网络拓扑考虑在内。但是,我们也可以注意到,由于CaGCN是一种非线性变换,对任意节点,它并不能保证和的类间序关系是一致的。换句话说,它并不能保持分类GCN的分类精度。针对这一点,接下来我们将对CaGCN进行改进。
精度保存的属性
首先,我们对一般的精度保存的校正函数进行了研究,提出了如下理论:
理论一:对于一个校正函数,一维函数以及节点的输出,如果是一个严格保序函数并满足
则是可以保存分类模型的精度。
Temperature scaling(TS)就是一个最简单的精度保存的校正函数,它用一个标量对所有节点的输出的所有维度做相同的变换:,这里的就是一个严格保序函数。因此我们可以借助TS的思想,对前面提出的CaGCN进行改进。具体来说,给定分类模型的输出,我们首先用CaGCN为每个节点学到一个,然后再进行TS变换。用公式可形式化的表示为:
相比于公式(2)中未改进的CaGCN,公式(4)的CaGCN可以保存分类模型GCN的精度;相比于TS方法,其为每个节点学习到了一种非线性变换,同时在校正过程中将网络拓扑考虑在内。需要注意的是,相比于公式(2)中的模型,公式(4)施加了很强的约束,它迫使中所有的维度只能进行相同的变换,但是接下来我们将证明他们在置信度校正方面的相等性。事实上,我们只要证明公式(4)可以输出中的任意一个置信度值即可,如下:
理论二:给定分类模型对任意节点的输出,假定对于的所有元素均不趋于无穷,则通过公式(4)得到的校正后的置信度可以取遍区间。
到此,我们提出的CaGCN已经可以满足需要的全部属性,即(1)考虑网络拓扑 (2)是一个非线性函数 (3)能保存分类GCN的分类精度。接下来我们将讲述CaGCN的目标函数。
优化目标
前人已经证明了优化NLL loss(交叉熵loss)便可以对置信度校正进行优化,因此我们也将NLL loss作为损失函数:
此外,由于NLL loss并不能直接减小错误预测的置信度,我们提出了一个正则化项:
其中,和分别指正确和错误预测的数量,和指预测概率向量的最大值和次大值。最终,目标函数为:
其中,为超参数。
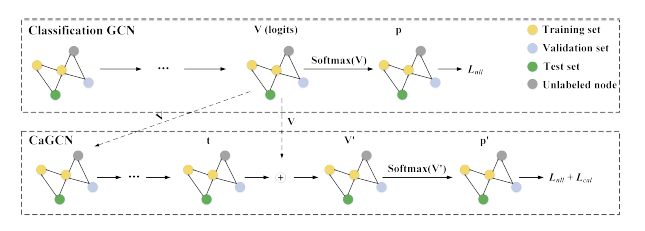
CaGCN整体的框架如图4所示,其中实线代表可以进行反向梯度传播的运算。我们首先利用训练集训练好一个分类GCN从而得到所有节点的输出,接下来以作为CaGCN的输入,利用验证集训练CaGCN。具体来说,首先将输入到CaGCN中得到每个节点的,然后对进行temperature scaling变换得到,即对于节点,,最后对做softmax变换并根据公式(5,6,7)得到目标函数,优化该目标函数从而更新CaGCN。
图4 CaGCN的整体框架3 基于置信度校正的自训练方法
这里我们额外提出一个置信度校正的实际应用,即将其用于改进GCNs中自训练方法。自训练指的是为无标签节点预测伪标签,然后选择部分高置信度节点连同伪标签加入到训练集,从而扩充训练集,改进模型性能的方法。由于GCNs普遍是不自信的,因此我们首先对GCN输出的置信度进行校正,然后再利用校正后的置信度选择无标签节点,从而更好利用正确的低置信的预测。我们将该方法称之为CaGCN-st。
4 实验
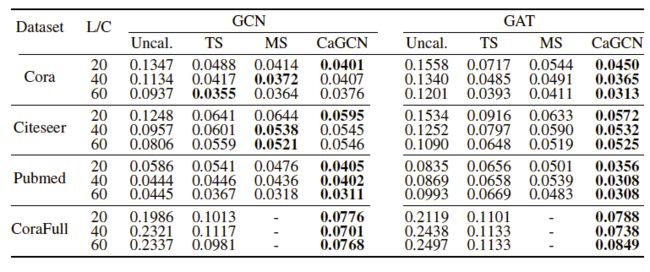
实验分为两部分,分别评估CaGCN在置信度校正方面的性能和CaGCN-st在提高模型分类准确率方面的性能,其中前者的评估指标是ECE,后者是Accuracy。两个实验均选择了Cora、Citeseer、Pubmed、CoraFull四个数据集,每个数据集选取了不同的标签率。实验结果如下:
图5 CaGCN与其他置信度校正方法的结果对比(值越小代表性能越好)
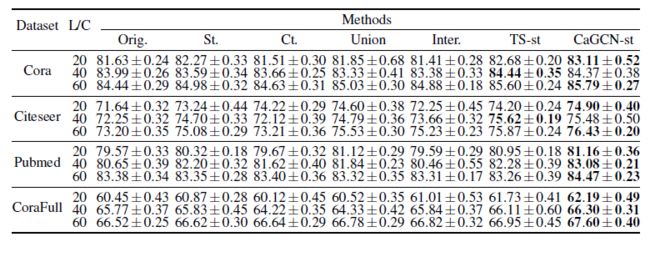
图6 CaGCN-st与其他自训练方法的结果对比(值越大代表性能越好)
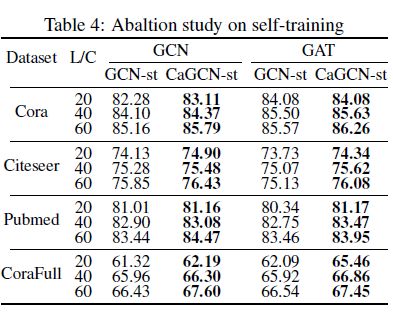
另外,我们还进行了CaGCN-st的消融实验,验证增加的置信度校正方法的有效性,结果如图7所示,其中GCN-st指没有置信度校正的普通自训练方法。
图7 自训练消融实验更多细节以及实验结果请参见:https://arxiv.org/abs/2109.14285
本期责任编辑:王啸
本期编辑:刘佳玮
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑黄海广老师《机器学习课程》视频课本站qq群851320808,加入微信群请扫码: