车间调度问题大全及编程思路(附遗传算法求解代码)
车间调度问题是典型的N-P问题,也是典型的带有复杂约束的离散优化问题.
车间调度问题一般而言是指有J个工件, 每个工件有Pj个工序, 有M个机器,工件j的第p个工序在机器m的加工时长为Tjpm,在满足加工工序前后约束的前提下,求一个加工方案,使得总的加工时间或制造跨度makespan最短.
从大类上而言,分为流水线调度(flow shop problem, fsp)和车间调度(job shop problem, jsp)
1.jsp
其特点是每个零件在机器上的加工顺序可以不一样, 加工时间也可以不同. 这类问题又分为普通车间调度jsp和柔性车间调度fjsp.
类型所需-工序数是否相同编码-是否只能在一个机器上加工编码
如jsp(1,1) 表示每个零件的工序数量相同, 且工序只能在一个机器上加工的jsp问题.
(1)普通jsp(jsp(1,1)和jsp(0,1)) jsp(1,1)
jsp(1,1):
每个零件的工序数量相同, 且工序只能在一个机器上加工
jsp(0,1):
每个零件的工序数量不相同, 且工序只能在一个机器上加工
(2)柔性jsp
jsp(1,n)
jsp(1,n) jsp表示fjsp问题, 第一个的1表示每个零件的工序数量相同, 第二个的n表示工序可以在n个机器上加工,且n对每个零件可以不同.
jsp(0,n)
jsp(1,n) jsp表示fjsp问题, 第一个的1表示每个零件的工序数量相同, 第二个的n表示工序可以在n个机器上加工,且n对每个零件可以不同.
2. jsp的一般求解方法
主要思路:采用双层编码
(1)第一层编码是工序的优先度编码
采用零件工序编码S和机器编码M的双层编码
有K个零件, 每个零件有pk个工序,那么工序编码S的长度n=p1 +p2…+pK, 且基因为1到n的一个不重复自然数排列。
并构造一个p1个1, p2个2, p3个3...的一个排列S0, S0中k的在序列中第m次出现则表示零件k的第m个工序在这一位置。
第一层编码是一个排序S,用该S对S0进行重排,得到一个新的排序S2
(2)第二层编码是为工序指派机器的编码
机器编码M长度也是n,其基因为该工序采用其第几个可用机器。
举例:
如k=2,p1=2, p2=4,n=6,M=3则 一个合法的染色体可表示为[3,4,1,5,2,6, 1,2,2,1,2,3]
S0=[1,1,2,2,2,2] 如果S=[3,4,1,5,2,6], 那么用S对S0重排后有S2=[2,2,1,2,1,2]
S2的意义为
第1位的2表示零件2的第1个工序
第2位的2表示零件2的第2个工序
第3位的1表示零件1的第1个工序
第4位的2表示零件2的第3个工序
第5位的1表示零件1的第2个工序
第6位的2表示零件2的第4个工序
机器编码M=[1,2,2,1,2,3]
第1位的1表示零件1的第1个工序用它的第1个可用机器加工
第2位的2表示零件1的第1个工序用它的第2个可用机器加工
第3位的2表示零件2的第1个工序用它的第2个可用机器加工
第4位的1表示零件2的第2个工序用它的第1个可用机器加工
第5位的2表示零件2的第3个工序用它的第2个可用机器加工
第6位的3表示零件2的第4个工序用它的第3个可用机器加工
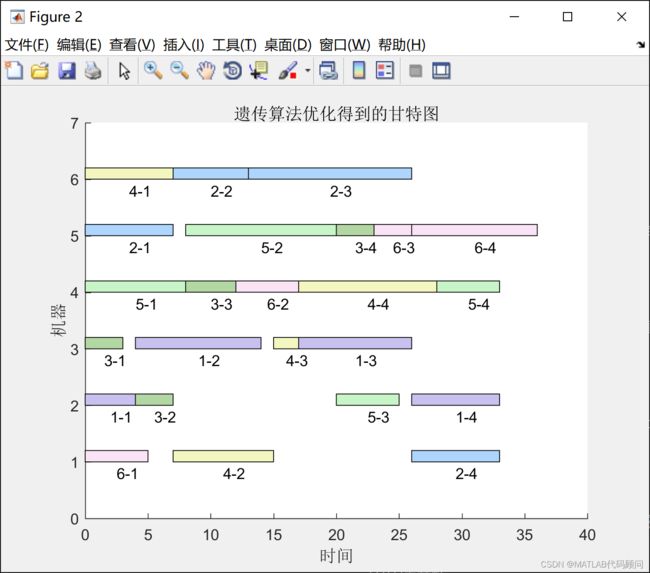
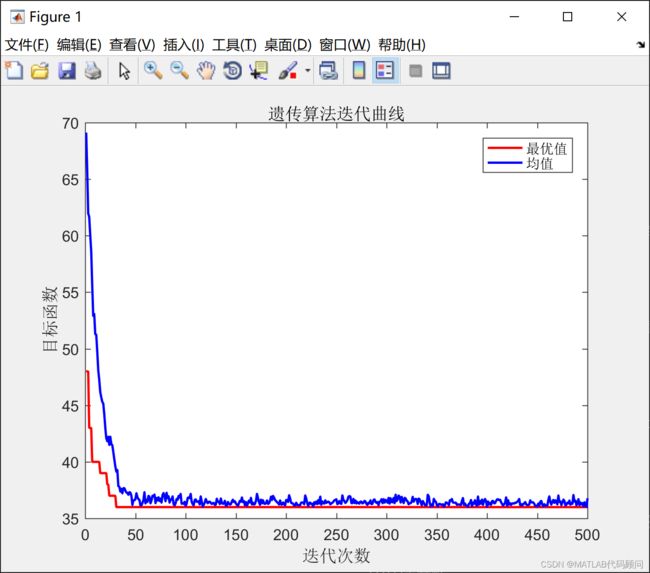
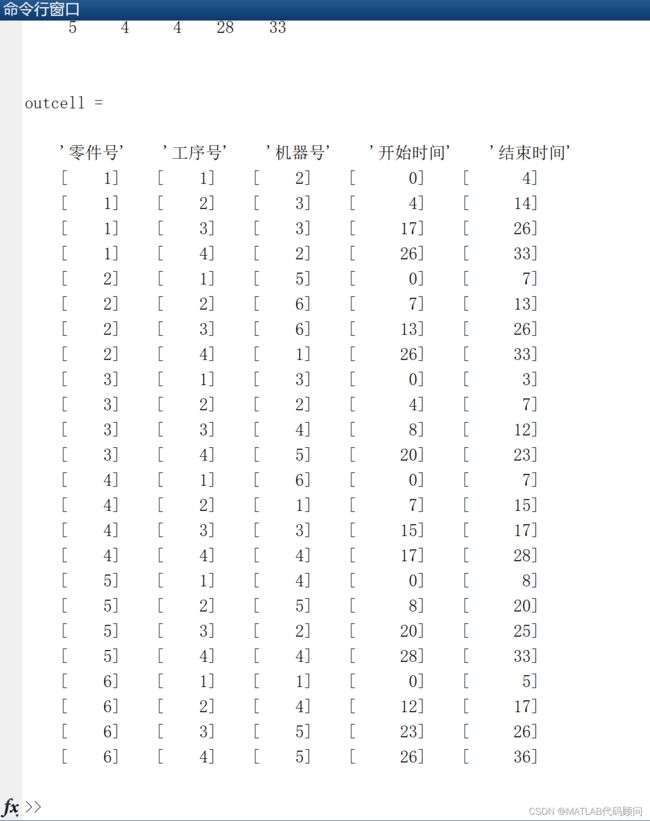
3.程序结果举例