数据结构--图（更新ing~）

  树具有灵活性，并且存在许多不同的树的应用，但是就树本身而言有一定的局限性，树只能表示层次关系，比如父子关系。而其他的比如兄弟关系只能够间接表示。

推广---  图

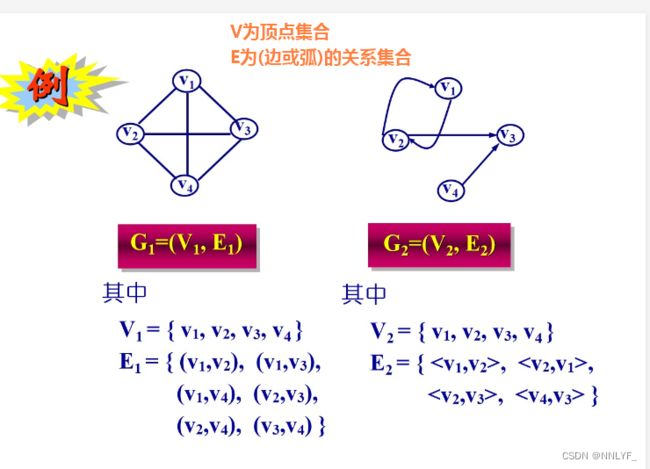
图形结构中，数据元素之间的关系是任意的。

一、图的基本概念

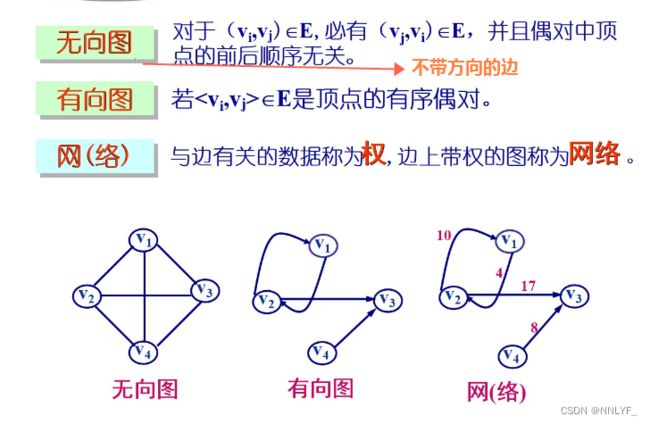
二、图的分类

三、图的相关术语

1、顶点的度

无向图：n个顶点找两条，没有方向，

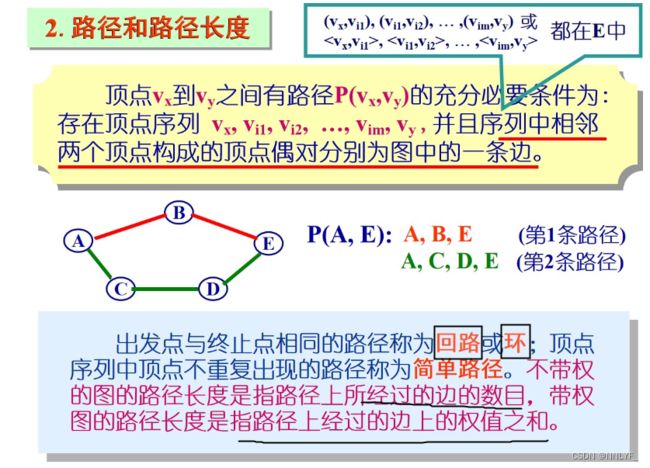
2、路径和路径长度

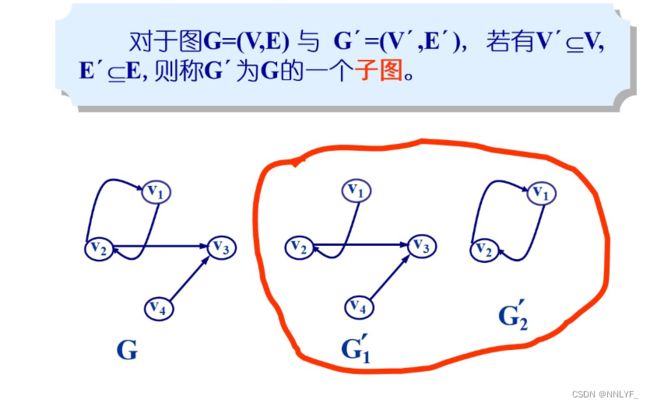
3.子图

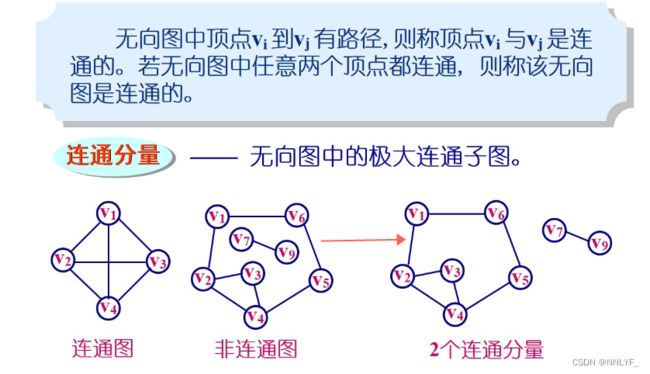
4.图的连通

1）无向图的连通

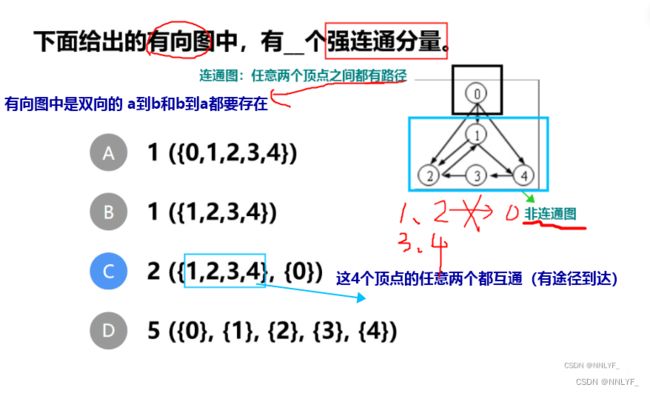
2）有向图的连通

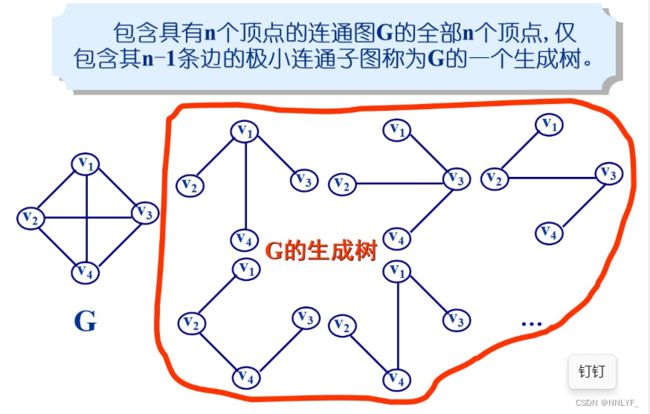
5.生成树

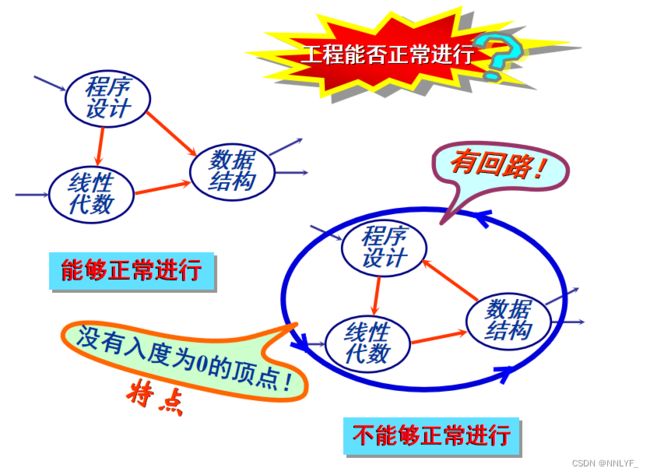
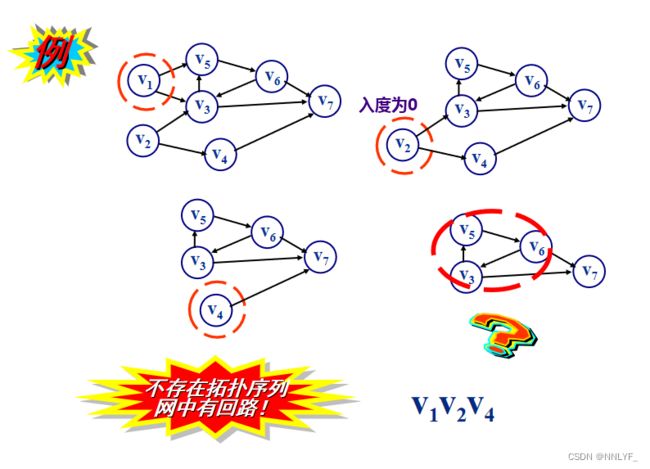
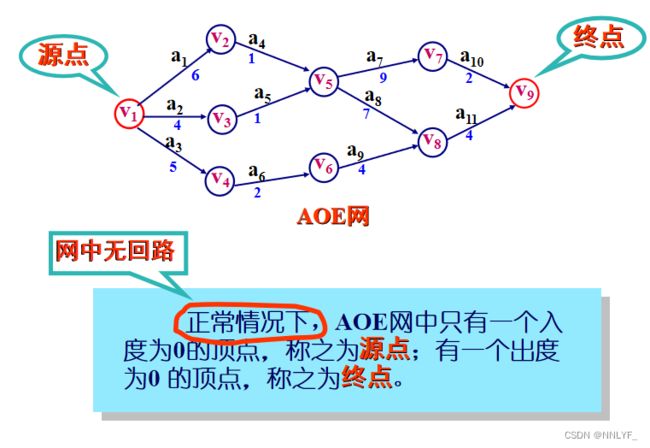
#不讨论的图：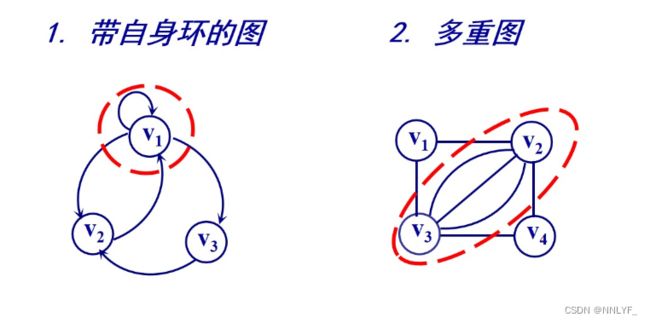

四、图的存储方法

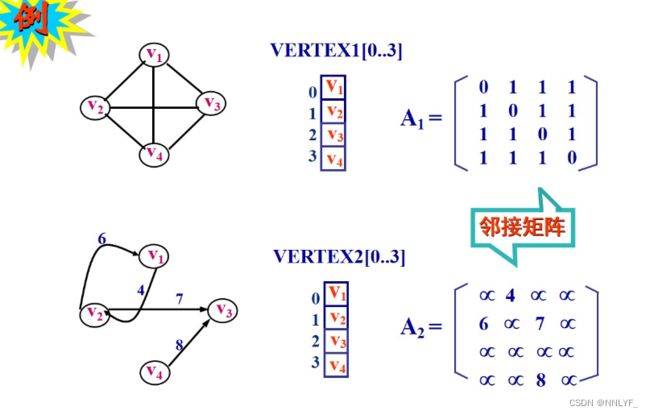
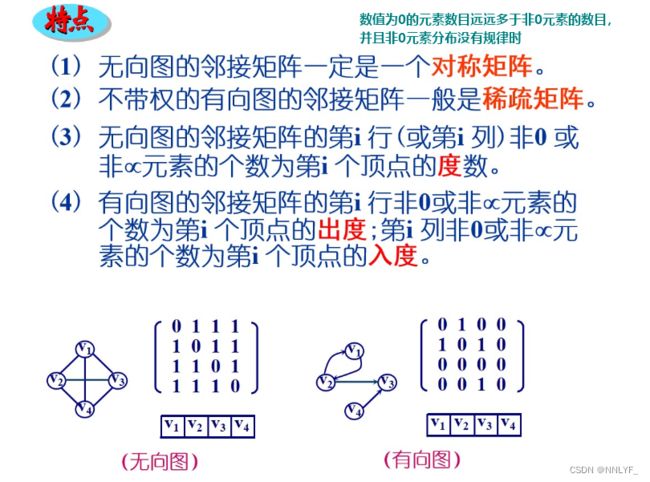
1、邻接矩阵存储方法

对称矩阵：

一个对称矩阵是指矩阵的主对角线两侧的元素相等。在这个矩阵中，通过观察可以发现对称性质：矩阵的第i行第j列的元素等于第j行第i列的元素。

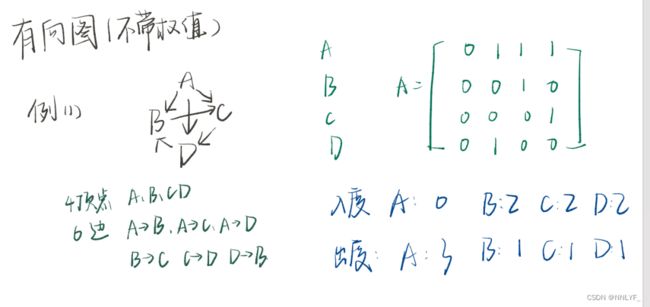
无向图的邻接矩阵一定是对称的。

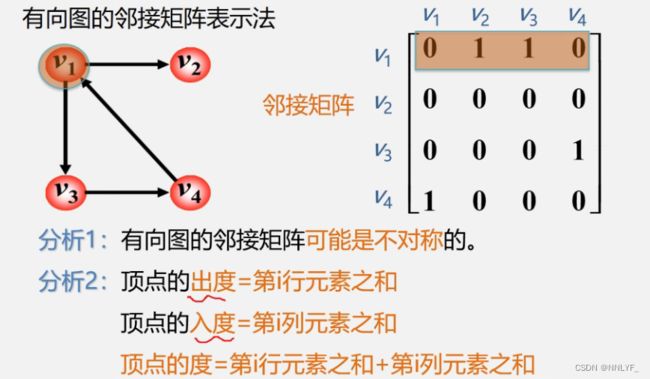
有向图的邻接矩阵一定是不对称的。

  有向图中每个节点之间的边是有方向的，因此如果节点i到节点j有一条有向边，那么邻接矩阵中第i行第j列的元素就为1或者权值，而第j行第i列的元素为0（无权值的情况）或者无穷（有权值的情况）。

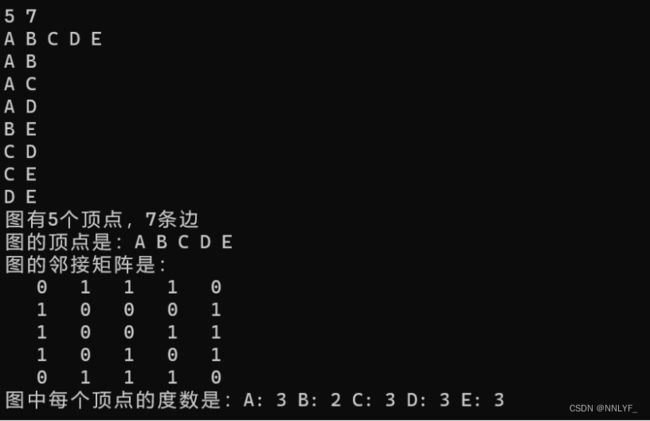
**无向图的邻接矩阵建图和度数输出（完整代码）

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}

adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
         //将顶点字符转换为对应的数组索引。
        // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
        // 可以得到对应的数组索引（0、1、2等）。   
        g.edge[n1][n2] = g.edge[n2][n1] = 1;
        //无向图，邻接矩阵对应的n1行n2列和n2n1列都赋值为1(邻接矩阵的对称性）
        //将对应的邻接矩阵元素设置为1，表示图中对应的顶点之间存在一条边。
    }

    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            printf("%4d", g.edge[i][j]);
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的度数是：");
    for (int i = 0; i < g.n; i++) {
        int degree = 0;
        for (int j = 0; j < g.n; j++) {
            if (g.edge[i][j] == 1) {
                degree++;
            }
        }
        printf("%c: %d ", g.vex[i], degree);
    }
    printf("\n");
}

输入样例：

**有向图邻接矩阵建图和度数输出（附完整代码）

修改的部分：

• 将g.edge[n1][n2] = g.edge[n2][n1] = 1; 修改为 g.edge[n1][n2] = 1; 表示从顶点n1指向顶点n2的有向边。
• 把无向图中的度数输出改成入度和出度输出

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}

adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
        //将顶点字符转换为对应的数组索引。
       // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
       // 可以得到对应的数组索引（0、1、2等）。   
        g.edge[n1][n2] = 1;
        //有向图，邻接矩阵对应的n1行n2列赋值为1
        //将对应的邻接矩阵元素设置为1，表示图中对应的顶点之间存在一条边。
    }

    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            printf("%4d", g.edge[i][j]);
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的入度是：\n");
    for (int i = 0; i < g.n; i++) {
        int indegree = 0;
            for (int j = 0; j < g.n; j++) {
                if (g.edge[j][i] == 1) {
                    indegree++;
                 }
            }
            printf("%c: %d \n", g.vex[i], indegree);
       }
       
  


    printf("图中每个顶点的出度是：\n");
    for (int i = 0; i < g.n; i++) {
        int outdegree = 0;
        for (int j = 0; j < g.n; j++) {
            if (g.edge[i][j] == 1) {
                outdegree++;
            }
        }
        printf("%c: %d \n", g.vex[i], outdegree);
        
    }

}

测试样例：

**有向带权图邻接矩阵建图和度数输出（含完整代码）

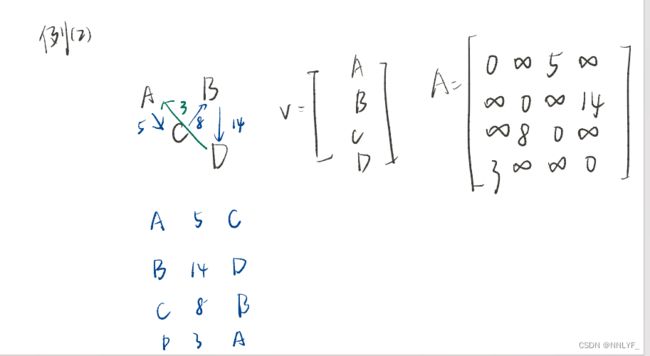
要注意有向图带权图中，含有权值的线路如 A 20 B ，反过来B到A就是 INF，不相连的两个顶点之间也是INF

**自环考虑为0的情况 **  实际情况和做题中通常考虑为无穷大

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量

typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型

typedef struct {
    int n, m; //n个顶点，m条边
    VexType vex[N];//一维数组存放所有顶点的数据信息
    EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;

//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息（顶点、邻接矩阵）
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);

int main()
{
    //1.建图
    adjGraph g = createGraph();
    //2.输出图的信息
    print(g);
    printDegree(g);
    return 0;
}


adjGraph createGraph()//建图
{
    adjGraph g;
    memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中，所有元素初始化为0
    // g.edge 邻接矩阵
    //sizeof(g.edge) 数组占用的总字节数
    scanf("%d%d", &g.n, &g.m);//输入顶点数和边数
    getchar();//吸收换行符
    //1.输入n个顶点
    for (int i = 0; i < g.n; i++) {
        scanf("%c ", &g.vex[i]);
    }
    //2.输入m条边，按照邻接矩阵存图 
    // 将邻接矩阵初始化为INF
    for (int i = 0; i < g.m; i++) {
        for (int j = 0; j < g.m; j++) {
            g.edge[i][j] = INF;
        }
    }
    for (int i = 0; i < g.m; i++) {
        char v1, v2;
        int weight;
        scanf("\n%c %d %c", &v1, &weight, &v2);//读入当前边的2个顶点
        int n1 = v1 - 'A', n2 = v2 - 'A';
        //将顶点字符转换为对应的数组索引。
        // 假设顶点标签是大写字母'A'、'B'、'C'等，通过将其减去字符'A'的ASCII码值
        // 可以得到对应的数组索引（0、1、2等）。
       
        if (n1 == n2) {
            g.edge[n1][n2] = 0;
        }
        else {
            g.edge[n1][n2] = weight;
            g.edge[n2][n1] = INF; // 反方向的边权值设置为INF
        }
    }


    return g;
}

void print(adjGraph g)
{
    printf("图有%d个顶点，%d条边\n", g.n, g.m);
    printf("图的顶点是：");
    for (int i = 0; i < g.n; i++) {
        printf("%c ", g.vex[i]);
    }
    printf("\n图的邻接矩阵是：\n");
    for (int i = 0; i < g.n; i++) {
        for (int j = 0; j < g.n; j++) {
            if (i == j) printf("0 ");
            else if (g.edge[i][j] == INF)
            {
                printf("INF ");
           }
            else  {
                   printf("%-4d", g.edge[i][j]);
            }
                  
        
            
        }
        printf("\n");
    }
}

void printDegree(adjGraph g)
{
    printf("图中每个顶点的入度是：\n");
    for (int i = 0; i < g.n; i++) {
        int indegree = 0;
        for (int j = 0; j < g.n; j++) {
     
                  if (g.edge[j][i] != 0 && g.edge[j][i] != INF) {
                     indegree++;
                 }
    
            
        }
        printf("%c: %d \n", g.vex[i], indegree);
    }




    printf("图中每个顶点的出度是：\n");
    for (int i = 0; i < g.n; i++) {
        int outdegree = 0;
        for (int j = 0; j < g.n; j++) {
                if (g.edge[i][j] != 0&& g.edge[i][j] != INF) {
                    outdegree++;
                }
            }

        
        printf("%c: %d \n", g.vex[i], outdegree);

    }

}

样例：

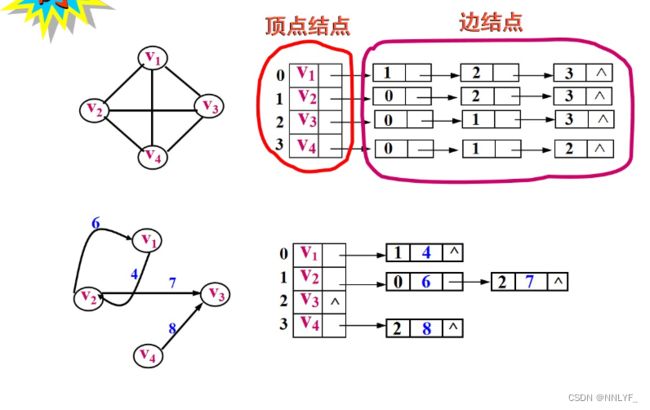
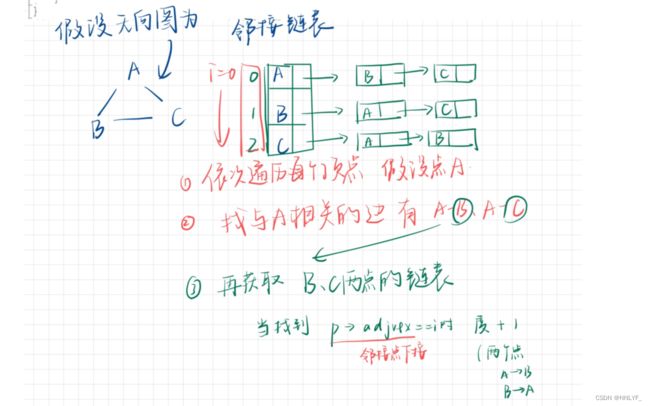
2、邻接表存储方法

  对每一个顶点建立一个单链表，将同一个顶点发出的边链接在一个称为边链表的单链表中。

头插法：

无向图中相连即放在链表里作为边结点（包含与该点相连的所有顶点）。

有向图按照方向选择结点作为边结点。‘’

** 邻接表计算顶点的度 函数

无向图：

void printDegree(adjListGraph graph) //无向图
{
    //计算每个顶点的度数
    for (int i = 0; i < graph.n; i++) {//遍历每个顶点
        int Degree = 0;

        //计算入度
        for (int j = 0; j < graph.n; j++) { //遍历所有顶点，寻找与当前顶点相关的边
            ELink* p = graph.vex[j].edge;//获取第KJj个顶点的邻接表
            while (p) {//遍历该邻接表中的所有边
                if (p->adjvex == i) {//如果当前边指向当前顶点
                    Degree++;
                    break;//跳出循环，继续计算下一个顶点的入度
                }
                p = p->next;//否则继续遍历该邻接表中的下一条边
            }
        }
  
        printf("顶点%c的度为%d\n", graph.vex[i].vertex, Degree);
    }
}

有向图：

void printDegree(adjListGraph graph) //有向图
{
    //计算每个顶点的度数
    for (int i = 0; i < graph.n; i++) {//遍历每个顶点
        int inDegree = 0;
        int outDegree = 0;
        //计算入度
        for (int j = 0; j < graph.n; j++) { //遍历所有顶点，寻找与当前顶点相关的边
            ELink* p = graph.vex[j].edge;//获取第j个顶点的邻接表
            while (p) {//遍历该邻接表中的所有边
                if (p->adjvex == i) {//如果当前边指向当前顶点
                    inDegree++;
                    break;//跳出循环，继续计算下一个顶点的入度
                }
                p = p->next;//否则继续遍历该邻接表中的下一条边
            }
        }
        ELink* p = graph.vex[i].edge;//获取当前顶点的邻接表
        while (p) {//遍历该邻接表中的所有边
            outDegree++;//记录当前顶点的出度
            p = p->next;//继续遍历该邻接表中的下一条边
        }
        printf("顶点%c的入度为%d，出度为%d\n", graph.vex[i].vertex, inDegree, outDegree);
    }
}

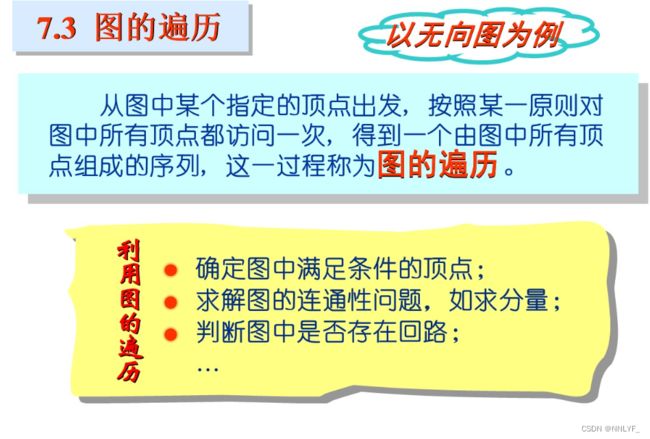
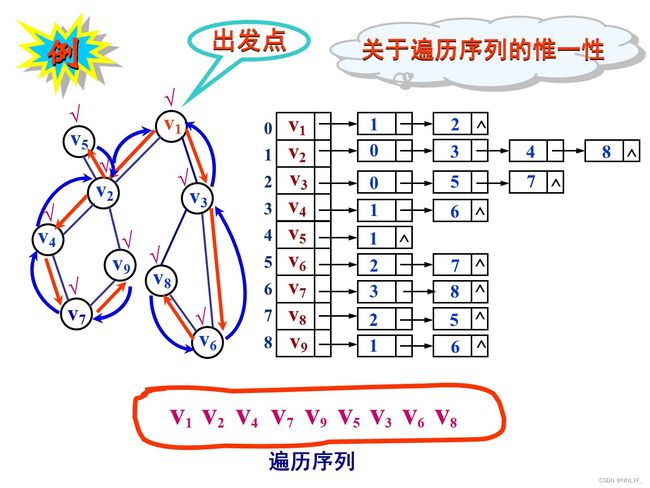
五、图的遍历

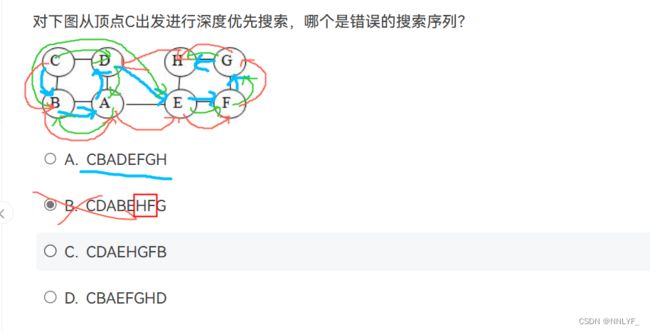
1.深度优先遍历

** 访问完顶点v以后访问的是v的邻接点，比如ABCD，访问了B，那下一步走A或者C都是可以的。

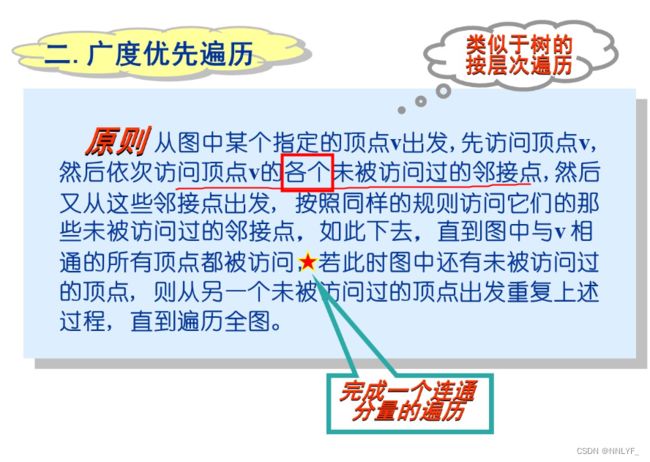
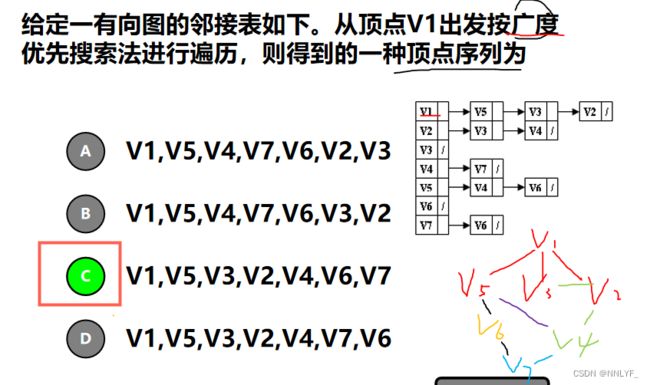
2.广度优先遍历

**无向图的创建、度的计算、dfs和bfs（完整代码）

#include 
#include 
#include 
#define N (100+5)
#define INF (0x3f3f3f3f) //定义INF为一个十六进制无穷大常量
typedef char vexType;//顶点类型
int visited[N];//状态数组，标记当前点有没有被访问过

//邻接边
typedef struct edge {
    int adjvex;//邻接点的下标，从0开始
    int weight;//边的权重
    struct edge* next;//下一个邻接点的地址
}ELink;


//邻接点
typedef struct {
    vexType vertex;//顶点的数据
    ELink* edge;//指向第一条依附于该顶点的边的指针
}VLink;

typedef struct {
    int n, m;//n个顶点，m条边
    VLink vex[N];//邻接点数组
}adjListGraph;
//1.邻接表建图
void createGraph(adjListGraph* graph);
//2.打印图
void printGraph(adjListGraph graph);
//3.输出图的度数（入度、出度、度数）
void printDegree(adjListGraph graph);
//4.1 深度优先遍历-从下标为n的点出发
void dfs(adjListGraph graph, int n);
//4.2 深度优先遍历-搜所有的点
void dfsAll(adjListGraph graph);
//5.1 广度优先遍历-从下标为n的点出发
void bfs(adjListGraph graph, int n);
//5.2广度优先遍历--搜所有的点
void bfsAll(adjListGraph graph);

//循环队列
#define M (1000+5)
typedef int ElemType;//队列元素类型
typedef struct {
    ElemType data[M];
    int front, rear;
}SqCyQueue;
//0.初始化队列
void init(SqCyQueue* q);
//1.队列是否为空，空则返回1，否则返回0
int isEmpty(SqCyQueue q);
//2.队列是否已满，满了返回1，否则返回0
int isFull(SqCyQueue q);
//入队 成功返回1，否则返回0
int push(SqCyQueue* q, ElemType item);
//出队 成功返回1，否则返回0
int pop(SqCyQueue* q, ElemType* item);

int main()
{
    memset(visited, 0, sizeof(visited));//visited 数组中的所有元素都赋值为 0，从而实现对数组的初始化
    adjListGraph g;
    createGraph(&g);
    printGraph(g);
    printDegree(g);
    int n = 0;//n不同就是从第n+1个点开始dfs或者bfs
   
    printf("\n从%c点出发深度优先遍历\n", g.vex[n].vertex);
    //从第一个点开始深度搜索
    dfs(g, n);
     printf("\n深度搜索所有点\n");
    dfsAll(g);
    
    printf("\n从%c点出发广度优先遍历\n", g.vex[n].vertex);
    bfs(g, n);
    printf("\n广度搜索所有点\n");
    bfsAll(g);
    return 0;
}

1.邻接表建图
(一）无向图
void createGraph(adjListGraph* graph)
{
    //1.输入n个顶点和m条边
    scanf("%d%d", &graph->n, &graph->m);

    //2.输入n个顶点，存入图邻接点数组中
    for (int i = 0; i < graph->n; i++) {
        //读入的字符数据是不是有效的
        while (1) {
            char c = getchar();
            if (c >= 'A' && c <= 'Z' || c >= '0' && c <= '9')
            {
                graph->vex[i].vertex = c;
                graph->vex[i].edge = NULL;//指针初始化为空
                break;
            }
        }
    }

    //3.依次输入m条边的2个顶点v1和v2
    for (int i = 0; i < graph->m; i++) {
        char v1, v2;
        scanf("\n%c %c", &v1, &v2);
        //在邻接点数组vex中查找v1和v2的下标k1和k2
        int k1 = -1, k2 = -1;
        for (int j = 0; j < graph->n; j++) {
            if (graph->vex[j].vertex == v1)
                k1 = j;
            if (graph->vex[j].vertex == v2)
                k2 = j;
        }
        //如果找不到对应的下标，说明输入的顶点信息有误
        if (k1 == -1 || k2 == -1) {
            printf("Error: invalid vertex information.\n");
            exit(0);
        }
        //以k2为下标创建邻接边
        //分配内存并初始化
        ELink* p = (ELink*)malloc(sizeof(ELink));
        p->adjvex = k2;
        p->next = NULL;
        //把这条边加到k1对应的邻接点
        if (graph->vex[k1].edge == NULL)
            graph->vex[k1].edge = p;
        else {
            ELink* tail = graph->vex[k1].edge;
            while (tail->next != NULL)
                tail = tail->next;
            tail->next = p;
        }

        //无向图的话，另加一条边，以k1为下标创建邻接边
        ELink* q = (ELink*)malloc(sizeof(ELink));
        q->adjvex = k1;
        q->next = NULL;
        if (graph->vex[k2].edge == NULL)
            graph->vex[k2].edge = q;
        else {
            ELink* tail = graph->vex[k2].edge;
            while (tail->next != NULL)
                tail = tail->next;
            tail->next = q;
        }
    }
}

// 2.打印图
void printGraph(adjListGraph graph)
{
    // 遍历图的n个邻接点
    for (int i = 0; i < graph.n; i++) {
        // 1.输出顶点数据
        printf("%c", graph.vex[i].vertex);
        // 2.输出当前邻接点关联的邻接边
        // 遍历链表
        ELink* p = graph.vex[i].edge; // 初始化为链表的表头
        while (p) {
            int t = p->adjvex; // 邻接点下标
            printf(" -> %c", graph.vex[t].vertex);
            p = p->next;
        }
        printf("\n");
    }
}
//3.输出图的度数

//（1）无向图
void printDegree(adjListGraph graph) 
{
    //计算每个顶点的度数
    for (int i = 0; i < graph.n; i++) {//遍历每个顶点
        int Degree = 0;

        //计算入度
        for (int j = 0; j < graph.n; j++) { //遍历所有顶点，寻找与当前顶点相关的边
            ELink* p = graph.vex[j].edge;//获取第KJj个顶点的邻接表
            while (p) {//遍历该邻接表中的所有边
                if (p->adjvex == i) {//如果当前边指向当前顶点
                    Degree++;
                    break;//跳出循环，继续计算下一个顶点的入度
                }
                p = p->next;//否则继续遍历该邻接表中的下一条边
            }
        }
  
        printf("顶点%c的度为%d\n", graph.vex[i].vertex, Degree);
    }
}




//4.1深度优先遍历-从下标为n的点出发
void dfs(adjListGraph graph, int n)
{
    visited[n] = 1; // 标记当前节点已被访问
    printf("%c ", graph.vex[n].vertex); // 输出当前访问的节点

    // 递归访问未访问过的邻接点
    ELink* p = graph.vex[n].edge;//将指针p指向下标为n的节点的邻接表链表头
    
    while (p) {//循环遍历所有与当前节点相连的未访问过的邻接点
   //这里通过遍历邻接表链表，依次访问所有与当前节点相连的邻接点。
   // 由于邻接表链表有可能为空，因此需要用while循环判断p是否为空。
        if (!visited[p->adjvex]) {
            dfs(graph, p->adjvex);
        }
        p = p->next;
    }
}

//4.2深度优先遍历-搜所有的点
void dfsAll(adjListGraph graph)
{
    memset(visited, 0, sizeof(visited)); // 初始化状态数组
    for (int i = 0; i < graph.n; i++) {
        if (!visited[i]) {
            dfs(graph, i); // 对未访问过的节点进行深度优先遍历
        }
    }
}

//5.1广度优先遍历-从下标为n的点出发
void bfs(adjListGraph graph, int n)
{
    memset(visited, 0, sizeof(visited)); // 初始化状态数组
    SqCyQueue queue;
    init(&queue); // 初始化队列

    visited[n] = 1; // 标记起始节点已被访问
    printf("%c ", graph.vex[n].vertex); // 输出起始节点
    push(&queue, n); // 将起始节点入队

    while (!isEmpty(queue)) {
        int front;
        pop(&queue, &front); // 出队
        ELink* p = graph.vex[front].edge;
        while (p) {
            if (!visited[p->adjvex]) {
                visited[p->adjvex] = 1; // 标记当前节点已被访问
                printf("%c ", graph.vex[p->adjvex].vertex); // 输出当前访问的节点
                push(&queue, p->adjvex); // 将当前节点入队
            }
            p = p->next;
        }
    }
}

//5.2广度优先遍历-搜所有的点
void bfsAll(adjListGraph graph)
{
    memset(visited, 0, sizeof(visited)); // 初始化状态数组
    for (int i = 0; i < graph.n; i++) {
        if (!visited[i]) {
            bfs(graph, i); // 对未访问过的节点进行广度优先遍历
        }
    }
}







//0.初始化队列
void init(SqCyQueue* q)
{
    q->front = q->rear = 0;
}
//1.判断队列是否为空
int isEmpty(SqCyQueue q)
{
    if (q.front == q.rear) return 1;
    else return 0;
}
//2.判断队列是否已满
int isFull(SqCyQueue q)
{
    return (q.rear + 1) % M == q.front;
}
//3.入队，成功返回1，否则返回0
int push(SqCyQueue* q, ElemType item)
{
    if (isFull(*q)) {
        printf("队列已满，入队失败\n");
        return 0;
    }
    q->data[q->rear] = item;
    q->rear = (q->rear + 1) % M;
    return 1;
}
//4.出队，成功返回1，否则返回0
int pop(SqCyQueue* q, ElemType* item)
{
    if (isEmpty(*q)) {
        printf("队列为空，出队失败!\n");
        return 0;
    }
    else {
        *item = q->data[q->front];
        q->front = (q->front + 1) % M;
        return 1;
    }
}

测试样例：

**有向图的创建、度的计算、dfs和bfs（完整代码）

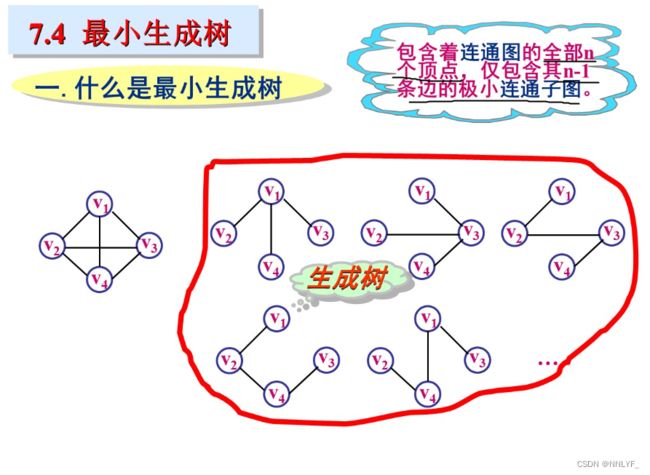
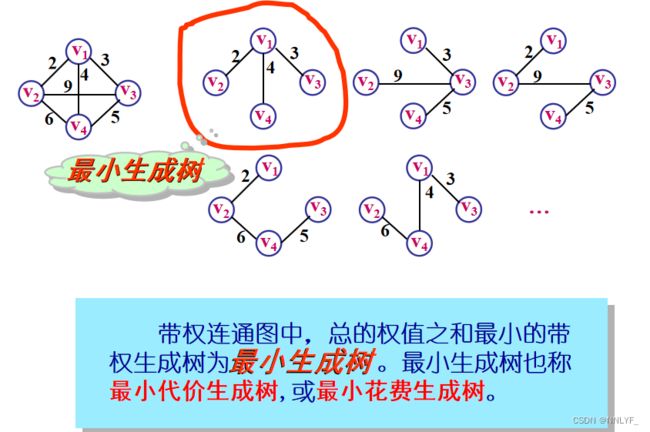
六、最小生成树

      

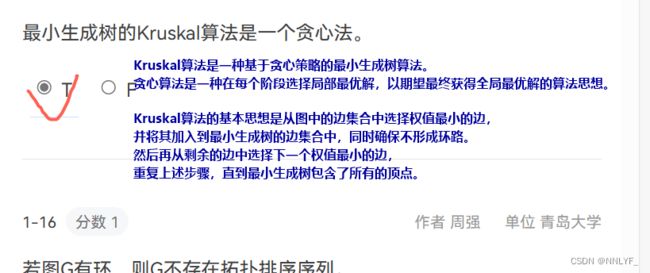
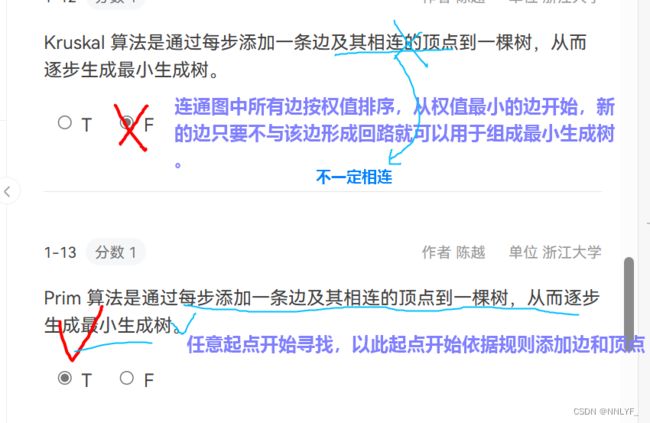
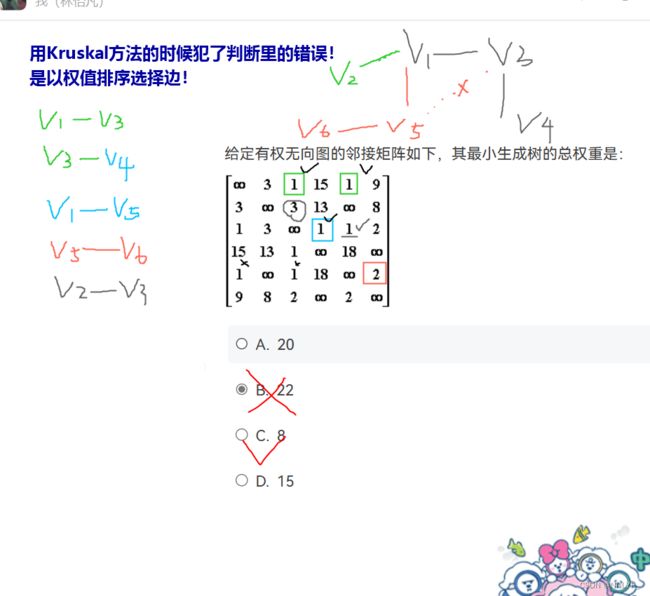
1.克鲁斯卡尔（Kruskal）方法

2.普里姆（Prim）算法

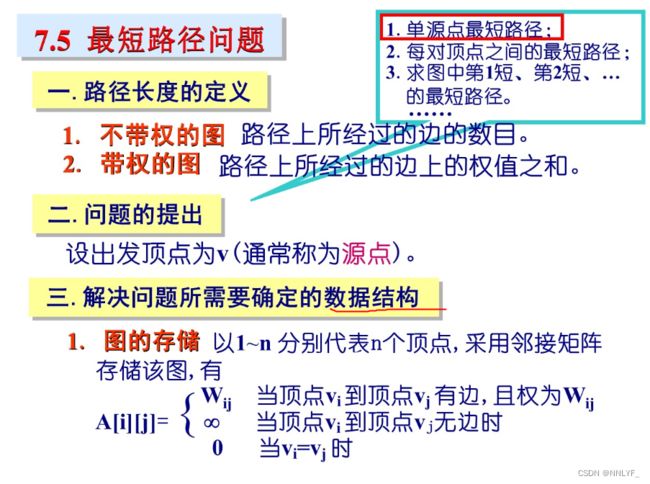
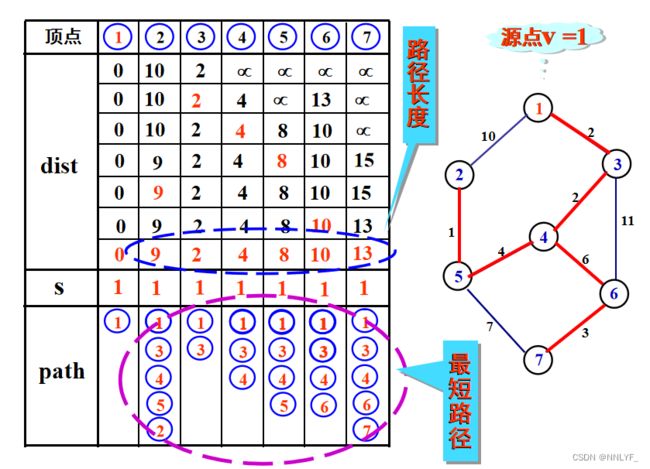
七、最短路径问题

一、Dijkstra算法（源点到某一顶点的最短路径）

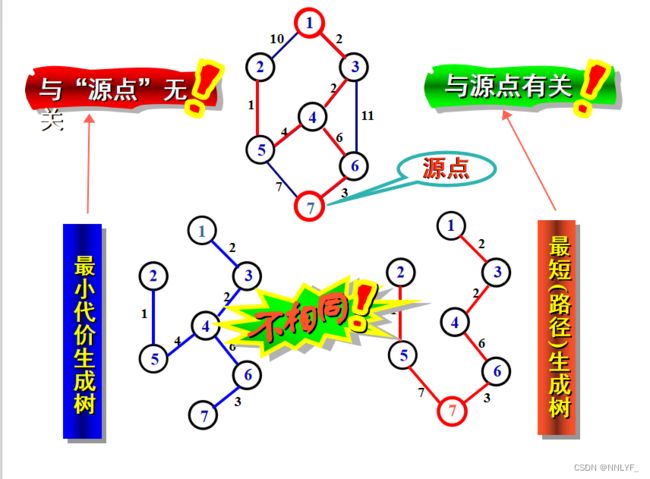
Q:对于对于给定的带权连通无向图，从某源点到图中各顶点的最短路径构成的生成树是否是该图的最小生成树？？

不一定相同。

二、Floyd算法（任意两个顶点之间的最短路径）

八、AOV网与拓扑排序

九、AOE网与关键路径

1、AOE网的定义

2、AOE网的特点

3、AOE网的存储方法

4、关键路径