归并排序(五)——归并排序的递归与非递归
目录
一.前言
二.归并排序
三.结语
一.前言
归并排序,本文全程高能,特别在涉及非递归的时候十分烧脑,大家加油~本文干货满满,高能不断,一定不要错过!码字不易,希望大家多多支持我呀!(三连+关注,你是我滴神!)
二.归并排序
基本思想:
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
如果它的左半区间有序,右半区间也有序,我们就能把它归并。那我们又应该如何将两个有序区间归并呢?
学过之前链表的都应该很熟悉,只需要不断取小的进行尾插就可以形成新的序列了。
对于不熟悉两个有序数组合并为一个有序数组的友友可以看看我这篇文章:https://mp.csdn.net/mp_blog/creation/editor/134120204
那我们现在要解决的就是如何让它左半区间有序,右半区间也有序。——对左半区间进行递归,也对右半区间进行递归。
4个分割2个,不断分割直到只剩下一个数为止。
我们在递进成1个数完成时开始回归的时候,一个数与一个数合并为有序,两个数与两个数合并为有序,最后回归的时候就是左半区间有序了,右半区间同理。
归并和我们快排的递归原理很像,只不过前者是后序,后者是前序。
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
首先开始归并的时候需要一个第三方数组,不能在原数组中归并。
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n - 1);//递归函数
free(tmp);
}
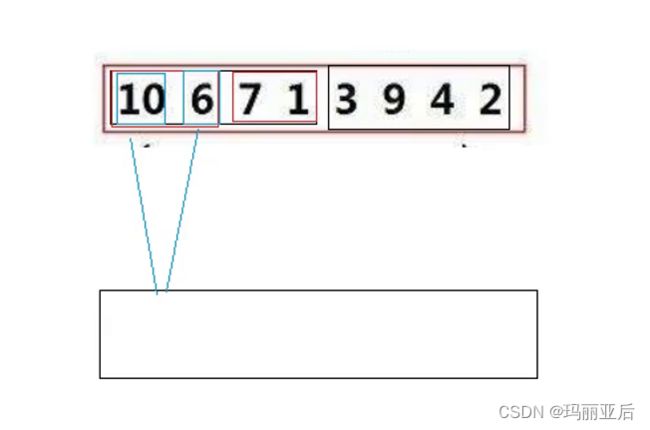
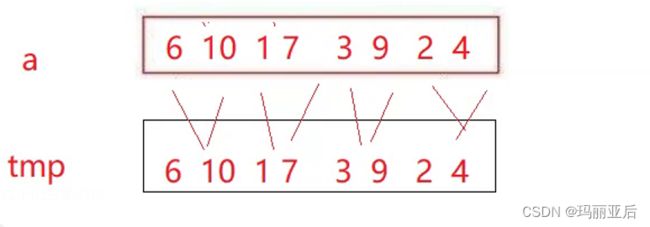
一开始的思路是把8个分成4个与4个让其有序
再把4个分成2个和2个让其有序
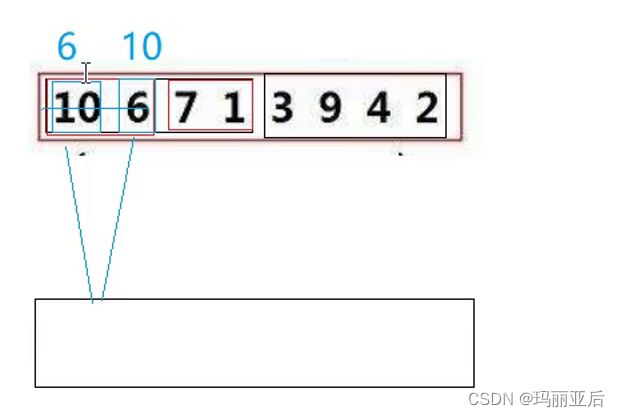
当2个分成1个和1个的时候,我们就发现一个数一定是有序的。那我们就把它拿下来归并。
拿到下面排好序后再拷贝回来。
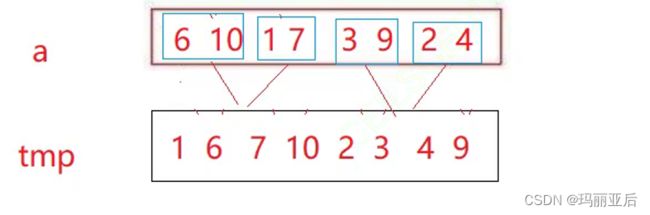
再把单独的7与1拿下来排好序,拷贝回去排好序的1 7。
因为6-10,1-7是两组有序的,再把它们拿下去排好序再拷贝回来,这样左半区间就有序了(1-6-7-10)。 右半区间同理。
现在回归到代码部分。
因为是走后序遍历,我们先分割数组(用mid)
void _MergeSort(int* a, int* tmp, int begin, int end)
{
//当只剩下一个数或没有数的时候,开始回归
if (end <= begin)
{
return;
}
int mid = (begin + end) / 2;
//划定范围[begin,mid][mid+1,end]
//开始分割,分割到一个数有序
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid+1, end);
//分割完毕时,开始进行两个有序序列合并,回归拷贝阶段
}
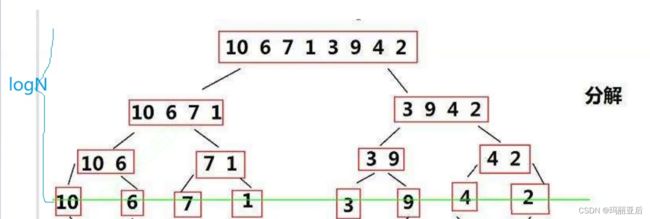
下面是递归展开图:
你归并的是从这段开始的区间,那自然也要把这段区间拷贝回去。
总代码:
void _MergeSort(int* a, int* tmp, int begin, int end)
{
//当只剩下一个数或没有数的时候,开始回归
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
//划定范围[begin,mid][mid+1,end]
//开始分割,分割到一个数有序
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid+1, end);
//分割完毕时,开始进行两个有序序列合并,回归拷贝阶段
//设置在tmp数组下的下标,方便进行取小插入
int begin1 = begin;
int end1 = mid;
int begin2 = mid+1;
int end2 = end;
int dex = begin;
//两个有序数组合并时,谁先取完数谁就停下
while (begin1 <= end1 && begin2 <= end2)
{
//取数开始比谁小
if (a[begin1] > a[begin2])
{
tmp[dex] = a[begin2];
dex++;
begin2++;
}
if (a[begin2] > a[begin1])
{
tmp[dex] = a[begin1];
dex++;
begin1++;
}
}
//因为我们在最后不知道哪一组先取完,所以我们最后要把没取完的那一组进行插入
while (begin1 <= end1)
{
tmp[dex] = a[begin1];
dex++;
begin1++;
}
while (begin2 <= end2)
{
tmp[dex] = a[begin2];
dex++;
begin2++;
}
//拷贝回去
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}时间复杂度:
高度遇到这种二分的数据基本是logN
每一层都要遍历N个数据,所以时间复杂度是标准的O(N*logN)
非递归:
我们能否像快排一样通过栈完成呢?
因为归并核心思想是后序,用栈不好控制。
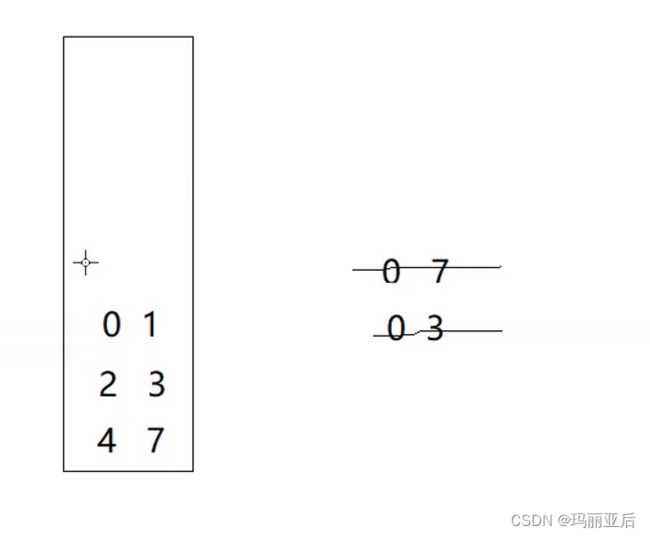
在0-7出栈后把4-7与0-3入栈
0-3取出,把2-3与0-1入栈
把0-1与2-3拿出来后就有序了,因为它们无法分割所以开始排序归并
接下来是4-7开始出栈,但我们可以发现左边的区间只是局部有序,并不是左半有序。这就是栈的弊端。
其实我们可以跳出归并的思想,采用类似斐波那契的方法,从头顺到尾。
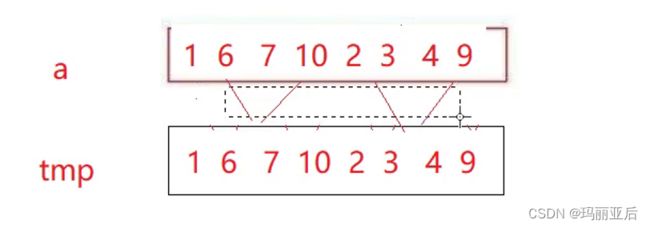
我们可以反向理解但都递归到最后一层时(只有一个数),两两归并然后准备拷贝回去的时候是下图所示:
1个数与1个数都归并且拷贝回去后:(目前是两两有序)
我们再让2个数与2个数开始归并
然后再拷贝回去。(目前是四个四个有序)
我们再让4个数与4个数进行归并:
我们设置gap,11归那gap就是1,22归那gap就是2
一开始gap为1的间隔,对这两组区间要进行归并
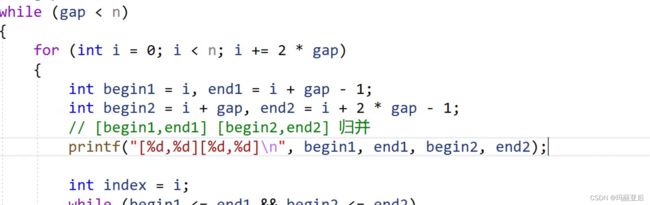
我们的循环只是控制了第一组,现在我们要如何控制在同一层gap的同时让范围往后走呢?
我们已经控制好范围了,接下来就是归并排序的代码(两个有序组取小),直接拷贝我们递归的取小代码。
void MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail"); return; } int gap = 1; for (int i = 0; i < n;i+=2*gap) { int begin1 = i,end1 = i + gap - 1; int begin2 = i + gap,end2 = i + 2 * gap - 1; //[begin1,end1][begin2,end2]归并 //不能再取begin,因为现在不走递归,所以要从原数组对应位置取小插入 int dex = i; //复制拷贝代码 while (begin1 <= end1 && begin2 <= end2) { //取数开始比谁小 if (a[begin1] > a[begin2]) { tmp[dex] = a[begin2]; dex++; begin2++; } if (a[begin2] > a[begin1]) { tmp[dex] = a[begin1]; dex++; begin1++; } } //因为我们在最后不知道哪一组先取完,所以我们最后要把没取完的那一组进行插入 while (begin1 <= end1) { tmp[dex] = a[begin1]; dex++; begin1++; } while (begin2 <= end2) { tmp[dex] = a[begin2]; dex++; begin2++; } //拷贝回去 memcpy(a + i, tmp + i, (2*gap) * sizeof(int)); } free(tmp); }
那么按照这个逻辑如果我们接下来要控制44归,88归的话只需要控制gap的取值就行了。
在每次排完后gao*2就好了。
void MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail"); return; } int gap = 1; while (gap < n) { for (int i = 0; i < n; i += 2 * gap) { int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //[begin1,end1][begin2,end2]归并 //不能再取begin,因为现在不走递归,所以要从原数组对应位置取小插入 int dex = i; //复制拷贝代码 while (begin1 <= end1 && begin2 <= end2) { //取数开始比谁小 if (a[begin1] > a[begin2]) { tmp[dex] = a[begin2]; dex++; begin2++; } if (a[begin2] > a[begin1]) { tmp[dex] = a[begin1]; dex++; begin1++; } } //因为我们在最后不知道哪一组先取完,所以我们最后要把没取完的那一组进行插入 while (begin1 <= end1) { tmp[dex] = a[begin1]; dex++; begin1++; } while (begin2 <= end2) { tmp[dex] = a[begin2]; dex++; begin2++; } //拷贝回去 memcpy(a + i, tmp + i, (2 * gap) * sizeof(int)); } //第一层11归并排完后开始下一层 gap = gap * 2; } free(tmp); }
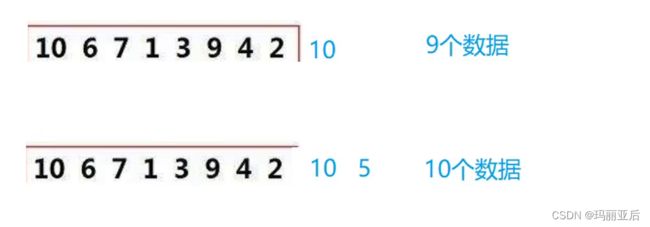
代码这样写其实还存在一些缺陷,比如当我们有9个数,甚至10,11个数据需要排序时:会出现越界问题
因为我们的范围都是由gap控制的,但是当9个数据11归时10没有与之对应的数组,但通过gap还是取到了它后面的下标,同理下面22归时gap也造成了数组越界问题。
所以这样按2的整数倍这样归并下去,必然会出现越界的问题。
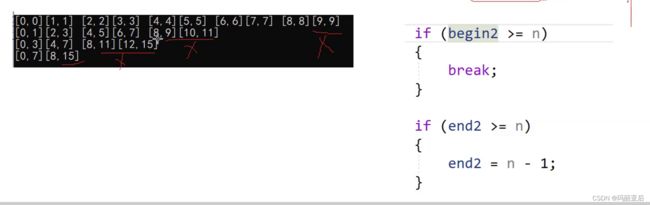
我们把所以情况的区间都打印出来分辨是否越界
这是正常的8个数
当我们输入9个值的时候,就出现了越界,11归就开始越界了
经过总结我们发现这三个范围定量是最容易出现越界的。
其实我们不用刻意去追求两两归并之类的,当end1越界了就不用回归了或end1没越界,begin2越界了。
当end2越界的时候我们就需要修正下标。
最后可以简化成这样,因为如果是end1越界,那后面也一定是越界的。所以只需要判断begin2就行了,反正它一越界就退出循环。
最后有一点要改的地方,2*gap明显是错误的
当我们有9个数的时候,最后88归时[8,8]可没有8个,而我们却开辟了16个空间。
其实应该是end2-begin1+1才是最终个数,但应该begin1在取小过程中发生++,所以只能用i来代替。
最后代码:
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1,end1][begin2,end2]归并
// 如果第二组不存在了,这一组就不用归并了
if (begin2 >= n)
{
break;
}
//如果第二组的右边界越界,修正
if (end2 >= n)
{
end2 = n - 1;
}
//不能再取begin,因为现在不走递归,所以要从原数组对应位置取小插入
int dex = i;
//复制拷贝代码
while (begin1 <= end1 && begin2 <= end2)
{
//取数开始比谁小
if (a[begin1] > a[begin2])
{
tmp[dex] = a[begin2];
dex++;
begin2++;
}
if (a[begin2] > a[begin1])
{
tmp[dex] = a[begin1];
dex++;
begin1++;
}
}
//因为我们在最后不知道哪一组先取完,所以我们最后要把没取完的那一组进行插入
while (begin1 <= end1)
{
tmp[dex] = a[begin1];
dex++;
begin1++;
}
while (begin2 <= end2)
{
tmp[dex] = a[begin2];
dex++;
begin2++;
}
//拷贝回去
memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));
}
//第一层11归并排完后开始下一层
gap = gap * 2;
}
free(tmp);
} 三.结语
三.结语
归并排序真是让人学得疯狂,特别是写非递归的时候要考虑太多东西啦,现在回头看看发现递归真的是小儿科了,希望大家珍惜好递归时光,因为非递归懂的都懂。最后感谢大家的观看,友友们能够学习到新的知识是额滴荣幸,期待我们下次相见~