第四部分第十二章：序列和时间序列

第四部分第序列，时间序列和预测

时间序列数据科学中最常用的技术之一，它具有广泛的应用—天气预报、销售预测、趋势分析等。本部分主要介绍时间序列的生成，并主要使用RNN、双向LSTM对时间序列进行预测。

• 序列和时间序列
• RNN网络样本的生成方法
• RNN时间序列预测
• 双向LSTM时间预测

本章将会学习通过计算机仿真的方法，生成带有一定随机性的时间序列的数据，也就是体现有一定周期变化的信号，如何和随机的信号叠加，从而能够模拟现实的一些随机的信号。
另外还会介绍如何对序列数据进行加窗处理，也就是进行编码，从而适应长短期记忆以及循环神经网络的训练要求。
还有将会学习搭建比较简单的多层的循环神经网络，这些网络还要和传统的时间序列的预测算法进行比较，也就是对循环神经网络要处理的时序信号而言，如何预测未来的取值，可以和传统的时间序列数据的预测算法进行比较。
还有还会学习如何搭建性能更高的双向的循环神经网络，也就是双向的长短期记忆网络，通过实验可以比较双向的循环神经网络或者说LSTM的性能，它的性能要比单向的循环神经网络更高一些，从而可以完成对时间序列处理的过程。在这个过程中，还要学会如何对网络的结构进行调参，例如学习率这些参数。通过调整可以查看模型性能的变化。

时序信号的生成：

1.时间序列介绍
时间序列是按照时间序列的一组随机变量，时间序列数据本质上反映的是某个或者某些随机变量随时间不断变化的趋势，而时间序列预测方法的核心就是从数据中挖掘出这种规律，并利用其对将来的数据做出估计，经济数据中大多数以时间序列的形式给出，根据观察时间的不同，时间序列中的书简可以是年份、季度或其他任何时间形式。
循环神经网络比较适合处理时序性数据。比如股票变化。

案例：
1.在本案例中，我们将首先生成一个趋势性时间序列。
趋势性（Trend):即在一定时间内的单调性，一般来说斜率是固定的。

2.在现实中，时间序列的信息往往具有一定的周期性，而且还会参杂一些随机信号。
时序信号是由一个周期性信号和一个随机信号，包括一些趋势信号组合而成的。
代码实现：
首先做一些图的声明

import numpy as np
import matplotlib.pyplot as plt

#定义两个函数，一个画图就是把时间序列可视化的函数plot_series，另外还有一个趋势性，也就是一个直线。
def plot_series(time, series):
    plt.figure(figsize=(10, 6))
    plt.plot(time, series)
    plt.xlabel("time")
    plt.ylabel("value")
    plt.grid(True)
    plt.show()
def trend(time, slope=0):
    return slope * time #斜率slope,

time = np.arange(4 * 365 + 1)#arange相当于一维数组生成的一个方法，365就是一年为1个周期，生成4个周期的数据。
baseline = 10 #baseline是基线，基线也是作为比较复杂的一个时序信号，基础的信号相当于一个水平线。
series = trend(time, 0.1)
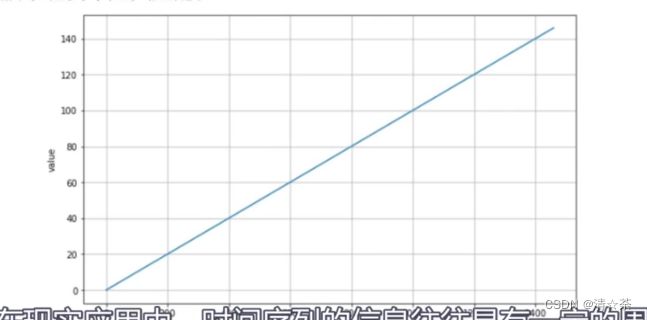
plot_series(time, series) #画出趋势性，横纵坐标。

比如time
趋势线就是斜率，斜率是0.1，纵向的series的value是乘以0.1得到的，比如time等于200所以series就是200*0.1，value的值就是20.

3.生成季节性时间序列：
然后，我们需要生成一个季节性的时间序列。季节性时间序列的特点是它有固定长度的变化，就想春夏秋冬的温度变化一样。季节性和周期性的区别在于，周期性的波动的时间频率是不定的。

# 生成季节性的时间序列
#定义了两个函数，seasonal_pattern就是一个具有周期性变化模式的时间序列数据。
#seasonality函数生成周期性的时间序列信号，
def seasonal_pattern(season_time):
    return np.where(season_time < 0.4,
                    np.cos(season_time * 2 * np.pi),
                    1 / np.exp(3 * season_time))

def seasonality(time, period, amplitude=1, phase=0):
    season_time = ((time + phase) % period) / period
    return amplitude * seasonal_pattern(season_time)

baseline = 10
amplitude = 40
series = seasonality(time, period=365, amplitude=amplitude)#调用语句，time就是前面定义的时间1400维的向量，时差period是365，amplitude是40就是整个信号在垂直方向，也就是在取值方向上它相当于振幅，
plot_series(time, series)

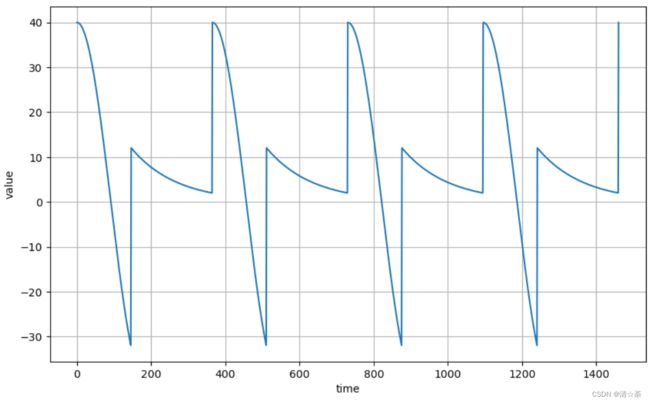
四个周期，非常规律的。但在现实中不会是这种情况，所以逐步增加一些其他信号来模拟。

slope = 0.05
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)#首先把刚才生成的信号，加上一个基线，然后再加上一个趋势信号。baseline相当于水平线，trend相当于斜率是0.05的趋势线，seasonality是刚才生成的周期性的时序信号。
plot_series(time, series)

有一定的朝上增长的趋势，另外它有周期性。

4.噪声的生成
在平常的时间序列分析中，时序数据会不可避免的含有噪声。噪声序列的特点表现在任何两个时点的随机变量都不相关，序列中没有任何可以利用的动态规律，因此不能用历史数据对未来进行预测和推断。因此，在这里我们也加入一些噪声对序列数据进行一定的干扰。

#增加一些白噪声。加了一个正态分布。
def noise(time, noise_level=1):
    return np.random.randn(len(time)) * noise_level#randn表示正态分布。noise_level表示随机信号强度的一个参数，它返回的值和时间有关，在不同的时间，我们要升上噪音水平，噪音水平越大，返回的值越大，噪声越强。
noise_level = 15 #噪声水平是15
noisy_series = series + noise(time, noise_level)
plot_series(time, noisy_series)

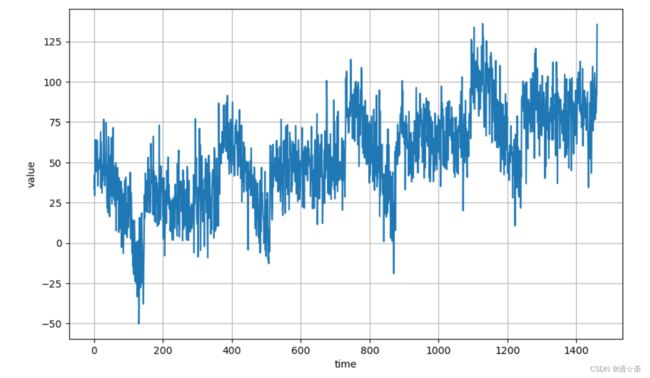
随着时间变化，这个周期性明显地变弱了。因为参杂了噪音信号，规律性降低了。

又生成了一个噪音信号，水平提高了：
从15变成40，有了更大的干扰。

noise_level = 40
noisy_series = series + noise(time, noise_level)
plot_series(time, noisy_series)

5.噪声的处理方法
由于噪声序列是没有意义的，所以我们需要尽量去除时间序列中的噪声，从而来减小其对我们预测时间序列产生的干扰。在这里，我们选用了平滑处理的方式，使用某一区间的加权和来替代原本噪声中的某个取值，下面的图片是经过处理后的噪声。
在实际项目里，怎么对噪声进行所谓的平滑处理？
第一种在原来含有噪声的信号的点，可以用加权和来替代原来的取值。

def autocorrelation(time, amplitude):
#rho1、rho2两个权重，
    rho1 = 0.5
    rho2 = -0.1
    ar = np.random.randn(len(time) + 50)
    ar[:50] = 100
    for step in range(50, len(time) + 50):
        ar[step] += rho1 * ar[step - 50]#把原来的值加上50
        ar[step] += rho2 * ar[step - 33]
    return ar[50:] * amplitude#乘以权重。使得信号和原来的信号振幅尽量相同，ar在0—1之间正态分布。

第二种平滑方法：

def autocorrelation(time, amplitude):
    rho = 0.8
    ar = np.random.randn(len(time) + 1)
    for step in range(1, len(time) + 1):
        ar[step] += rho * ar[step - 1]#某一个时间点的取值，在它的基础上加上0.8的前一个时刻的取值。
    return ar[1:] * amplitude

#调用第二个函数，实参是time和10，

series = autocorrelation(time, 10)
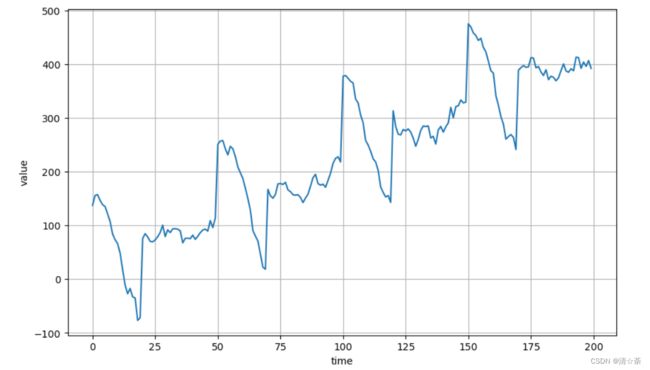
plot_series(time[:200], series[:200])#0~199

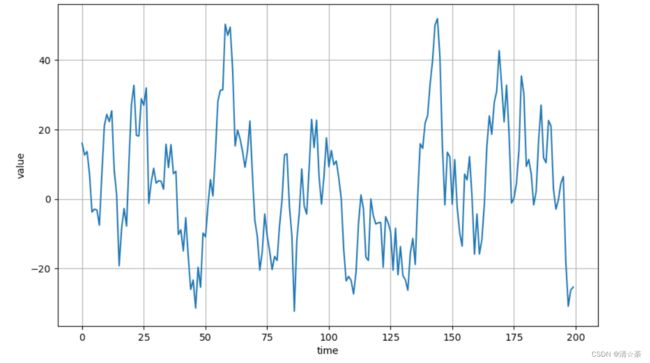
这个序列只展示前面200个时刻点，做过平滑处理随机信号好很多。

series = noise(time)#生成一个噪声信号，调用了noise函数，
plot_series(time[:200], series[:200])

均值为0，方差一般为1

#噪声再加一个趋势
series = autocorrelation(time, 10) + trend(time, 2)
plot_series(time[:200], series[:200])

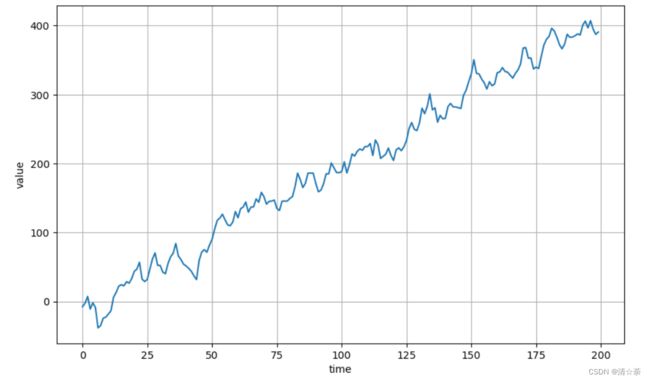
它是有一定的趋势变化的一个随机信号，生成一个斜率比较大，数值为2的趋势性。

#和刚才的周期性的信号叠加起来
series = autocorrelation(time, 10) + seasonality(time, period=50, amplitude=150) + trend(time, 2)
plot_series(time[:200], series[:200])

趋势开始具有周期性。

series = autocorrelation(time, 10) + seasonality(time, period=50, amplitude=150) + trend(time, 2)
series2 = autocorrelation(time, 5) + seasonality(time, period=50, amplitude=2) + trend(time, -1) + 550#series2就是对刚定义的序列信号参数做了修正，
series[200:] = series2[200:]
#series += noise(time, 30)
plot_series(time[:300], series[:300])

趋势和周期性优化了。
该程序为了预热使用，为后续如何用循环神经网络、长短期记忆、双向的LSTM处理时序信息做准备。然后进行预测，对过去或者将来的曲线进行预测。
步骤共两步：
第一步:生成一个含有不同噪声水平、具有周期性的时序信号。由多种信号组成，包括基线、趋势线、周期性信号以及正态分布的噪声组成的
第二步：模拟现实项目，对其进行了简单的平滑处理。

时间序列预测方法（移动平均）

1.时间序列的生成

在预测时间序列之前，我们需要生成一个时间序列。按照上一节课的知识，我们生成一个含有噪声的时间序列，如图。

# 生成有季节成分和趋势成分的时间序列
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras

def plot_series(time, series, format="-", start=0, end=None):
    plt.plot(time[start:end], series[start:end], format)
    plt.xlabel("Time")
    plt.ylabel("Value")
    plt.grid(True)

def trend(time, slope=0):
    return slope * time

def seasonal_pattern(season_time):
    """Just an arbitrary pattern, you can change it if you wish"""
    return np.where(season_time < 0.4,
                    np.cos(season_time * 2 * np.pi),
                    1 / np.exp(3 * season_time))

def seasonality(time, period, amplitude=1, phase=0):
    """Repeats the same pattern at each period"""
    season_time = ((time + phase) % period) / period
    return amplitude * seasonal_pattern(season_time)

def noise(time, noise_level=1, seed=None):
    rnd = np.random.RandomState(seed)
    return rnd.randn(len(time)) * noise_level

time = np.arange(4 * 365 + 1, dtype="float32")   #1461
baseline = 10
series = trend(time, 0.1)  
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5

# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=42)

plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()

横坐标是时间，纵坐标就是序列取值。

2.划分数据集

得到了时间序列后，我们需要将时间序列划分为训练集和检验集。训练集的作用在机器模型的案例中是来拟合模型，在本章节中在后续中没有用到。而验证集的作用则是用来检验模型的效果，在本章节中用于评估后续预测方法的准确性。

前1000作为训练集，剩下的序列样本作为校验集。

split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]#从split_time开始，一直到最后1461，
plt.figure(figsize=(10, 6))
plot_series(time_train, x_train)
plt.show()

plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plt.show()

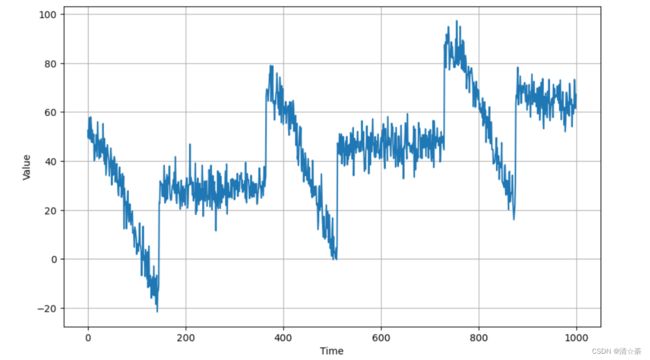
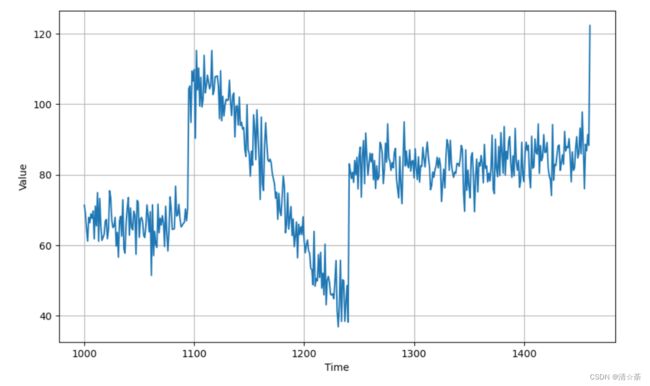
第一个图是训练集0_{999,第二个图是校验集1000}1461。

对时间序列进行预测：

3.朴素预测法预测时间序列

首先我们使用朴素预测法来预测时间序列，即把前一个时刻的时序值作为后一个时刻的预测值，某一段时刻内的预测值如图。得到完整的序列后，我们使用均方误差和平均绝对误差来评估预测的结果。

# 使用朴素预测法进行预测

naive_forecast = series[split_time - 1:-1]#校验曲线往右平移了一个时间单位。

plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, naive_forecast)

把上图做了一个扩展，一个room.

plt.figure(figsize=(10, 6))
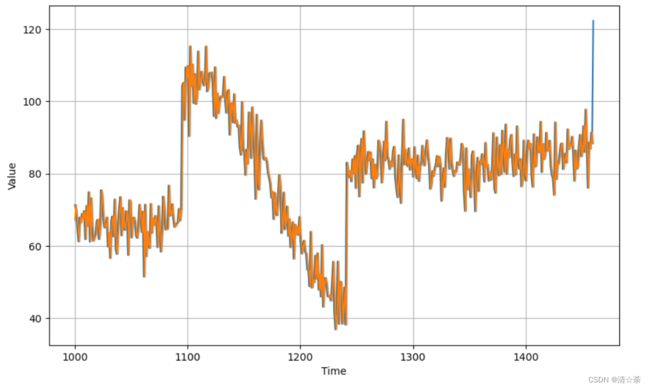
plot_series(time_valid, x_valid, start=0, end=150)
plot_series(time_valid, naive_forecast, start=1, end=151)

很明显的趋势，下图中的黄色线全部都是预测值组成的，蓝的都是原来真实的校验集。误差很小，只是有一个相位差，在垂直方向比例做了改动，通过调整start和end来实现。

# 计算误差

tf.compat.v1.enable_eager_execution()
print(keras.metrics.mean_squared_error(x_valid, naive_forecast).numpy())#平均绝对误差
print(keras.metrics.mean_absolute_error(x_valid, naive_forecast).numpy())#均方误差

4.移动平均法预测时间序列

我们再使用移动平均法来预测时间序列，移动平均法是用最近某一区间内时刻值的均值来预测未来时刻的值。直接对时间序列预测的预测结果如左图，可以看到其效果并不好。因此我们做了一些改进，最终得到右图的预测结果。

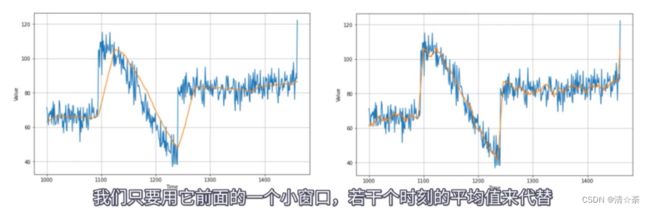
采用移动平均法来预测进行优化：

# 使用移动平均法进行预测
#定义一个函数叫moving_average_forecast，
def moving_average_forecast(series, window_size):
  """Forecasts the mean of the last few values.
  #实际上就是校验集窗口往前移动一个步长。
     If window_size=1, then this is equivalent to naive forecast"""
  forecast = []
  for time in range(len(series) - window_size):#series减去窗口，实际上就是时间序列往前移一个窗口
    forecast.append(series[time:time + window_size].mean())
  return np.array(forecast)

#某一个时刻它前面或者后面一个窗口的点做预测，
moving_avg = moving_average_forecast(series, 30)[split_time - 30:]#窗口大小为30，调用这个函数可以得到一个数组，校验集中的每一个时刻的预测值用列表表示，然后将列表转化成数组。校验集预测的时候用的是训练集最后30个时刻取值的平均值。
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, moving_avg)

# 计算误差
print(keras.metrics.mean_squared_error(x_valid, moving_avg).numpy())
print(keras.metrics.mean_absolute_error(x_valid, moving_avg).numpy())

# 去除趋势或周期性
diff_series = (series[365:] - series[:-365])#相减是只留下误差的信号，在校验集中的每一个时刻点，都只保留随机误差信号，diff_series提取随机误差
diff_time = time[365:]
plt.figure(figsize=(10, 6))
plot_series(diff_time, diff_series)
plt.show()

#对随机误差的信号做移动平均，黄线就是趋势线。
diff_moving_avg = moving_average_forecast(diff_series, 50)[split_time - 365 - 50:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, diff_series[split_time - 365:])
plot_series(time_valid, diff_moving_avg)#蓝的是真实的
plt.show()

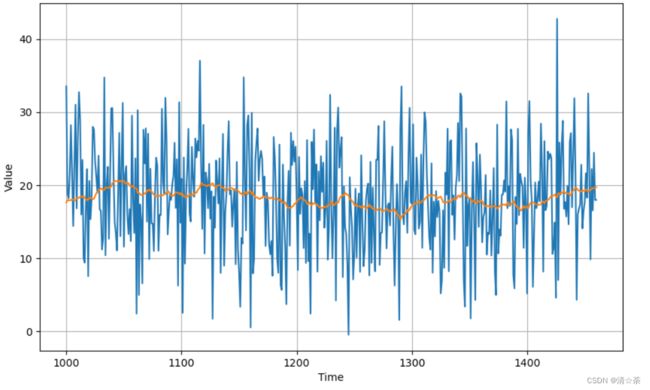
思路就是不对原来的周期性信号做移动平均，而对组合的误差的信号做移动平均，

#对正态分布的信号做移动平均，对误差信号做移动平均。
diff_moving_avg_plus_past = series[split_time - 365:-365] + diff_moving_avg
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)#真实的校验集数据
plot_series(time_valid, diff_moving_avg_plus_past)#优化后的数据。
plt.show()

# 计算误差
print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_past).numpy())#均方误差
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_past).numpy())#平均绝对误差

52.97366
5.839311

# 使用0均法来消除部分噪声，使用移动平均法来消除部分噪声。
diff_moving_avg_plus_smooth_past = moving_average_forecast(series[split_time - 370:-360], 10) + diff_moving_avg
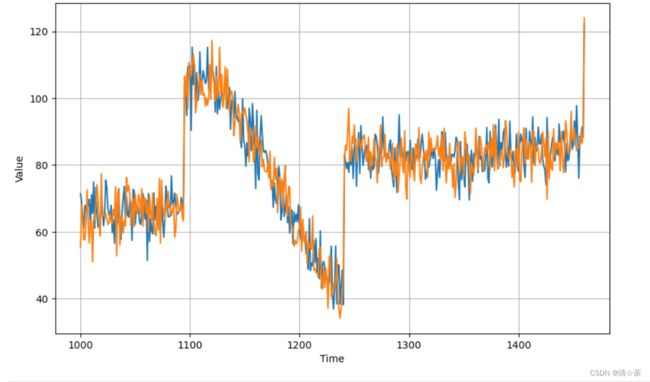
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, diff_moving_avg_plus_smooth_past)
plt.show()

print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())

33.45226
4.569442