奇妙的带环链表

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

前言

一、什么是带环链表？

二、带环链表的相关问题

1.带环链表1

2.带环链表2

总结

---

前言

带环链表作为链表结构中非常重要的一部分，其奇妙之处真的是耐人寻味，下面就让我们来一起深入了解一下吧。

---

一、什么是带环链表？

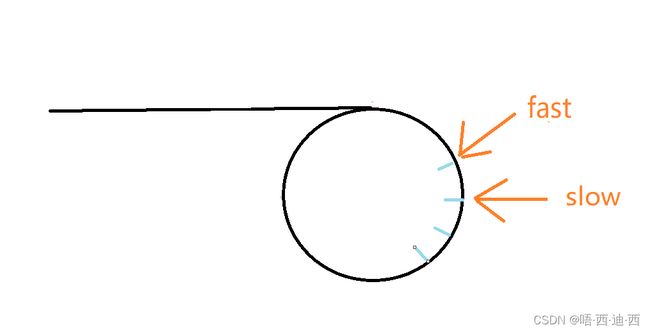
正如其名，带环链表就是在普通链表的基础上自身形成了环状结构，如下图所示：

其中（-4）中存储的是（2）的地址，自然形成了环状结构，且此时链表中是不存在尾节点的。

二、带环链表的相关问题

1.带环链表1

题目：141. 环形链表 - 力扣（LeetCode）

题意即是让我们判断一个链表是否带环，在这里我们可以使用快慢指针的思路进行解题。

建立快指针 fast 和满指针 slow，初始都指向链表的头 head，让 fast 一次走两步，让 slow 一次走一步，那么如果是带环链表的话，一定会在某一时刻 fast 会”追上“ slow。如果链表不带环，那么 fast 最终一定会变为空指针（NULL）。

问题一：为什么 fast 一定会”追上“ slow ，它们会不会在环中错过呢？

结论：fast 一定会追上 slow ，它们不会在环中错过。

证明：

        两指针大致变化如下图：

当 slow 刚进入环时，fast 可能已经在环里转了几圈了，也可能一圈都没转，这取决于环的长度，我们把这几种情况一起处理，不妨设此时 fast 与 slow 之间的距离为x（如图所示），因 fast 每次走两步，slow每次走一步，那么每走一次，fast 与 slow 之间的距离就会-1，则走一次 fast 与 slow 之间的距离变为 x-1，再走一次，fast 与 slow 之间的距离变为 x-2，易知，走x次后，fast 与 slow 之间的距离变为 0 ，即 fast ”追上了“ slow。到此问题一已经得到了解决。

问题二：为什么 fast 一定要一次走两步？能不能一次走三步或四步或更多呢？

结论：若 fast 一次走 n 步 （n>2），slow 还是一次走一步，那 fast 不一定能在环中再次”追上“slow，或者说它们在环中不一定能够相遇.

证明：

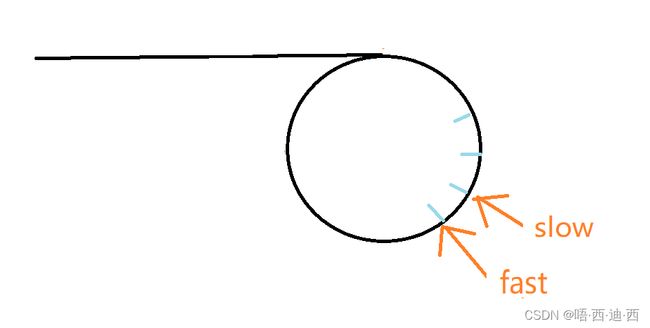
我们假设n=3，同样的，假设 slow 刚进入环时，fast 与 slow 之间的距离为 x，易知走一次后，它们之间的距离变为 x-2，再走一次变为x-4。

  1.      若x为偶数，则它们的距离变化过程为：

           x -> x-2 -> x-4 -> ...... -> 4 -> 2 -> 0

           距离为0代表 fast 与 slow 再次相遇，即 fast ”追上了“ slow。

 2.        若x为奇数,，则它们的距离变化为：

           x -> x-2 -> x-4 -> ...... -> 5 -> 3 -> 1 -> (-1)

            我们发现这里的距离从 1 直接变成了（-1），这代表着 fast 与 slow 并没有直接相遇，而是fast 直接跑到了 slow 前面 ，如下图所示：

        我们不妨设环的长度为 C，那么此时 fast 与 slow 之间的距离就变成了 C-1，然后又重新开始了 fast 努力追赶 slow 的过程，有已证可得若C-1为偶数的话，那么 fast 与 slow 将在第二轮的追赶中相遇，若C-1为奇数的话，那么每次 fast 都会恰好与 slow 错过，直接跑到了它前面，那么 fast 与 slow 将永远不会相遇。到此我们已经证明了问题二中的 n=3的情况，其他的情况也是类似的证明方法，这里就不一个一个列举了。 

        解决了这两个问题，相信大家都对该题的解法有了清晰的了解，接下来就是大家熟悉的敲代码环节了，AC代码奉上：

bool hasCycle(struct ListNode* head) //141.环形链表
{
	struct ListNode* fast, * slow;
	fast = slow = head;
	while (fast && fast->next)  //若为空，则不含环
	{
		fast = fast->next->next;
		slow = slow->next;
		if (fast == slow)
			return true;
	}
	return false;
}

        其中 while 的判断条件中因 fast 一次走两步，所以链表（不含环）的长度是奇数还是偶数对结束的条件有影响，故判断条件有两个。

2.带环链表2

题目：142. 环形链表 II - 力扣（LeetCode）

该题在上一题的基础上更深入了一些，如果是带环链表的话要让我们找到环的入口

---

对于该例子，2 就是环的入口。

解决这一题我们需要沿用上一题的思路， 由上题代码我们已经可以找到 fast 与 slow 相遇的点 meet，我们只需要让一个指针从链表的头部，另一个指针从 meet 点开始，两个指针同步移动，即一次都走一步，那么它们一定会在环的入口相遇。

证明：

对于一个带环链表，我们假设其未成环部分长度为L，环长为C，并由上题假设它们相遇于meet，设 meet 与环的入口间的距离为 X，如图：

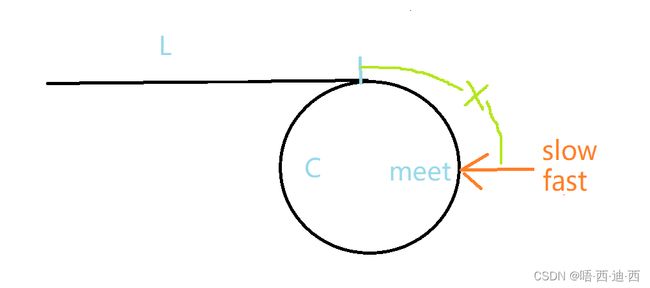 则从开始到它们相遇，slow 一定是在走完一圈之前与 fast 相遇，因为假设 slow 走完了一圈还没与 fast 相遇，那么 fast 一定走了至少两圈，那么它们一定相遇过了，与假设相矛盾，故 slow 一定在走完一圈之前就与 fast 相遇。则相遇时：

slow 走过的距离为：L+X；

fast 走过的距离为：L+N*C（表示fast可能再相遇前已经转了好几圈了）+X；

根据slow与fast的定义，可得： 2*（L+X）= L+N*C+X；

可解得：L=N*C-X；可写为：L=（N-1）*C+C-X;

那么一个指针A从链表头开始走，另一个指针B从 meet 开始走，同步前进，当A走了L时（刚好走到环的入口处），B也走了L，而L=（N-1）*C+C-X；即B转了N-1圈后又走了C-X（也刚好走到了环的入口处），即A与B会在环的入口出相遇。到此，这个问题也被完美的解决了。

理清思路后代码都不是事啦

struct ListNode* detectCycle(struct ListNode* head) //142.环形链表二---牛客
{
	struct ListNode* fast, * slow;
	fast = slow = head;
	while (fast && fast->next)
	{
		fast = fast->next->next;
		slow = slow->next;
		if (fast == slow)//有环
		{
			struct ListNode* meet = slow;

			while (head != meet)//有结论
			{
				head = head->next;
				meet = meet->next;
			}

			return meet;
		}
	}

	return NULL;
}

总结

        经过上面的学习，相信已经对带环链表有了一定的认识，如果觉得有收获的话记得点赞收藏加关注哦qwq