【文献阅读】AutoMap：Diagnose Your Microservice-based Web Applications Automatically

论文链接AutoMap:Diagnose Your Microservice-based Web Applications Automatically

前言（务必看一下~）

最近查看故障相关论文，发现故障根因这一块在微服务中也有诸多涉及。微服务场景下各项服务也具有多项检测数据，服务之间的拓扑结构也是异常复杂。因此，希望通过这篇文章的思想来探究故障根因分析。但是，这篇出自2020年的文章，至今没有一篇文章对该论文做出比较详细的讲述，笔者希望能够将本文章所述的方法尽量简单明了的展示给大家。

摘要部分

主要说明三点。
（1） 微服务是具有高度复杂性和动态性，静态故障排除方法无法适应频繁变化的情况。
（2） 服务之间存在故障传播，所以需要动态的故障诊断机制。
（3） 单一类型的指标不足以表征不同服务器中的异常。
所以AutoMap通过以下三种方法来解决上述问题。
（1） 定义一种“异常行为图”来描述微服务之间动态且复杂的拓扑结构。
（2） 定义两个二元运算，以及行为图上的相似函数来帮助AutoMap选取适当的诊断目标。
（3） 通过启发式的方法来进行游走，以实现故障原因的定位。

引言部分

探究了微服务故障排除算法的难点集中在：
（1） 动态的应用程序结构。以往静态的方法诸如阈值的方法，在微服务环境下无法获取适用于频繁变化的情况。
（2）间接异常传播，随着微服务架构中组件粒度变小，服务驻留在分布式主机和容器上，它们调用过程可以像直接调用一样同步。因此，异常的传播不再受调用依赖限制。如此，即使未被调用的微服务发生异常，也可能影响同一主机或容器中的其他服务，并且导致异常的传播。如下图所示，红色是故障源，黄色是受影响的服务，绿色的实线和虚线是同步和异步调用关系。（不理解没关系，知道会发生故障传播即可）

（3） 多种类型的度量。基于单一指标的算法无法识别根本原因，因为单衣类型的指标肯定是不足以表征不同服务中发生的异常的。（即缺乏先验知识，无法知道具体的采用哪几项指标来描述服务性能）

相关工作部分

该部分主要介绍前人的方法，此处省略。主要讲作者从前人的工作中总结到的经验，包括如下几点：
（1）MS-Rank提出了基于历史诊断记录来生成动态自适应的诊断机制。
（2）NetMedic、Sherlock都注意到另外一个关键问题，如何选取合适的指标类型。
（3）通过启发式的方法来进行故障定位。
所以AutoMap的工作主要做出如下几个贡献：
（1）通过行为图的概念以及一些计算方法，反映服务正常情况与异常情况下的统计特征。
（2）针对特定异常场景下的度量指标自动选择机制。
（3）真实场景下的验证。

问题陈述

问题定义

微服务的Web应用程序和以往故障诊断的场景类似，都是”黑盒”，只能够获取到几种类型的监控指标，但是不了解任何系统知识。现假设一个场景，在事件周期 $l$ 中，前端服务$V_{fe}$ 中观察到异常（即故障现象）。其中，$n$ 是服务数量，$m$是指标类型（即观测了m种监测指标）。目标是识别导致故障现象的一组服务$r_c$ （即故障原因）。

模型部分

模型整体

AutoMap算法具体的步骤如下：
（1）选择原始指标的采样间隔参数；
（2）使用多种类型的指标构建行为图；
（3）通过定义的“+”，“-”运算提取异常的轮廓，即异常模式图。
（4）进行启发式的根本故障原因检测算法。
（5）验证结果并计算精度
（6）更新度量权重矩阵，如果出现新的异常就重复上述过程。
重点关注 步骤三 与 步骤四。

模型采样间隔

简单来说就是，保证在该采样间隔过程中，每个服务平均被调用一次。

• 如果间隔过大，会导致有效波动的流失。
• 如果间隔过小，会导致冗余。

所以通过请求频率加权平均的方式得到最终的采样间隔。

行为图的构建（重点）

（1）将一个服务视作为一个节点，讲所有服务构建成一个无向完全连接图，$G(V,E,W)$，其中$W_{ijk}=1$ 的意思是，对于任意的一组服务$i,j$在第 $k$ 项观测值下的连接强度。
（2）**构建完全图：**在每个度量值下，例如下图在$M_{lat}$ 延迟的角度下进行判断。在$level=0$中，判断Dashboard与Event、AI之间是条件独立的，在$level=1$中，判断Event和AI是基于Dashboard条件独立的，由此可知，$level$是控制住“条件数目”的变量。后面$level=2$、$level=3$的情况都是同理。通上述方法可以将无向完全图转变为一个无向不完全图。
（3）**方向判断：**再通过三条规则进行方向的判断，（以往的方法都没有对连边方向进行判定，只是得知有无连边即可），根据规则一和方向的排列组合，可以得知，最终的行为图应为下图中绿色连线。
（4）计算权重更换不同观测值的视角，如图中表格所示，如果在其他观测值中也存在相同连边，则记为1，反之为0，最终做归一化得到该连边的权重。

加法操作以获得服务正常运行的特征

注：文中是Service Profile，我这里翻译成服务特征是结合了对于文章的理解，如下图红色下划线标注的。因为实际上就是得到了一个描述Service的特征情况，同时文章中此处还介绍了要将服务进行分类的一个过程，但是对实验影响不大，有兴趣的读者可以自行观看。

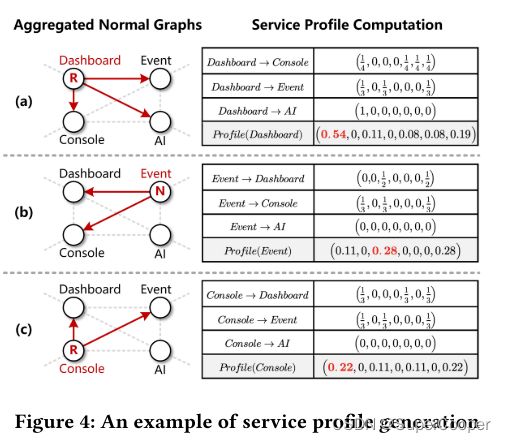
加法操作的定义：使用正常指标绘制数十个行为图，并将它们聚合以显示服务的特征。具体算法流程如下，即图的相加。

一个具体的例子，做法就是将所有连边加起来做平均，其中R,N是分类后的标签，不用太在意~

减法操作以获得服务异常运行的特征

事实上，在现实世界的事件中，只有少数服务会导致异常传播。由于很大一部分服务与异常无关，最初构建的行为图可能包含冗余服务和相关性。考虑到服务特征文件仅描述正常状态下的相关性，需要从行为图中删除这些冗余相关性。从而使得行为图更加贴合异常的描述。

下面是一个例子，很好理解，就是将与正常情况下相同的连边关系进行删除，得到“纯异常行为图“

小结：通过”加法操作“得到正常情况下的服务特征图；通过”减法操作“得到异常情况下的服务特征图。得到这两项，就是得到了服务之间的拓扑结构。

自动故障根因诊断

自动度量权重学习

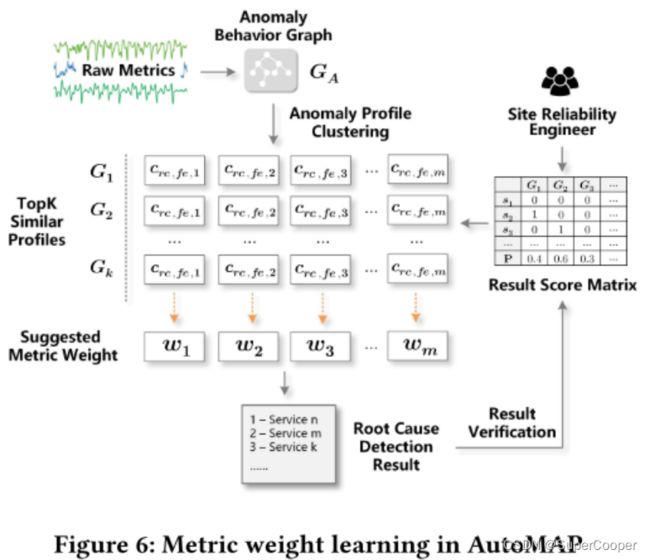
在AutoMaP中，如前面所提到的选择合适的诊断指标的基本思想是从经验丰富的工程师手动故障排除的方式中得出的。也就是说，如果历史事件中已确认的根本原因在某些指标上与前端服务显示出较高的相关性，则在类似情况下，候选根本原因服务也应该在相同指标下具有较高的相关性。为此，AutoMaP引入了基于特征(Profile)相似度的度量权重学习机制。
$c_{i,j,k}$表示在第$k$个度量下，$i,j$之间的相似度，以下图来说明如何使用历史信息的。
（1）利用原始观测值，使用之前提到的方法构建异常行为图。
（2）通过这个异常行为图可以计算得出一个异常特征，通过在【不同监测指标】下计算异常行为图中【故障原因】与【故障现象】之间的关系。如$G_1$中一行中的$c_{re,fe,1}$ 是在历史记录$G_1$指标1的情形下，计算根因之间的关联分数。
（3）得到相似分数后，就按照$\frac{1}{k}{\sum }_{j=1}^{k}P(G_j{)}_{c_{rc,fr,i}}$ 计算每个观测指标的权重值。（公式就是在将之前的关联分数求和再求平均，从而得到权重）

特征相似度计算

主要就是通过公式计算出两个图的相似度，具体可以看原文，Step1计算共享特征，Step2计算共享节点，Step3计算共享边。最终通过这三个指标值计算相似程度。文章中还举了一个例子。

故障源探因

采用的是启发式自动游走的方式，简单来说就是三部分，前向游走、自回游走，后向游走。

总结

该方法或将可以作为我们其他邻域故障诊断的框架式方法。从构建图的方法、通过相似度利用历史记录的方法进行诊断、以及最终通过启发式游走的方法来获取故障传播链路的方法，都是目前比较成熟，比较常用的方法。（这一篇文章由于距离看的时间太久啦，就简单的把一些我认为重要的部分给主要介绍了一下，有些不重要的我就省略了，还请大家见谅~）

致谢

感谢热心市民斌！！！