有限元分析简单实例之四杆结构（matlab）
有限元分析简单实例之四杆结构（matlab）
- 问题描述
- 要用到的函数
- 解答步骤
问题描述
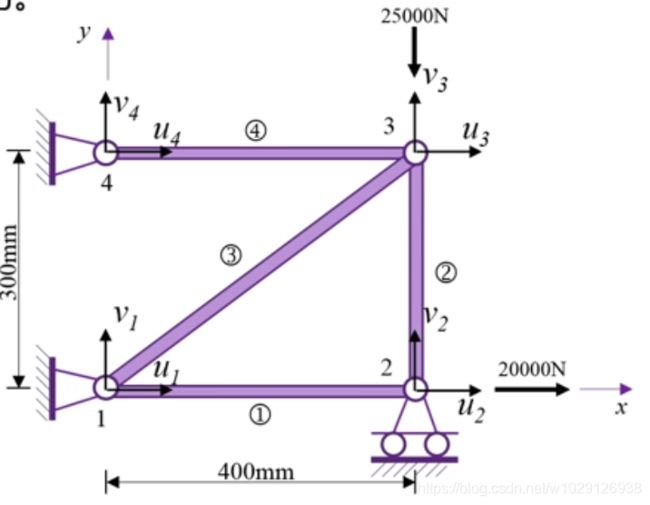一个四杆结构，施加如图所示的两个带有方向的力，对其进行有限元分析。
要用到的函数
（1）计算单元的刚度矩阵
function k = Bar2D2Node_Stiffness(E,A,x1,y1,x2,y2,alpha)
% 计算单元的刚度矩阵
% 输入弹性模量E，横截面积A，第一个结点的坐标（x1,y1）第二个节点的坐标（x2,y2）,角度alpha
% 输出单元刚度矩阵k(4*4)
L= sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
x = alpha*pi/180;
C=cos(x);
S=sin(x);
k = E*A/L*[C*C C*S -C*C -C*S;C*S S*S -C*S -S*S;-C*C -C*S C*C C*S;-C*S -S*S C*S S*S];
end
(2)进行单元刚度矩阵的组装
function z = Bar2D2Node_Assembly(KK,k,i,j)
% 该函数进行单元刚度矩阵的组装
% 输入单元刚度矩阵k，单元节点编号i,j
% 输出整体刚度矩阵KK
DOF(1)=2*i-1;
DOF(2)=2*i;
DOF(3)=2*j-1;
DOF(4)=2*j;
for n1=1:4
for n2=1:4
KK(DOF(n1),DOF(n2))=KK(DOF(n1),DOF(n2))+k(n1,n2);
end
end
z = KK;
end
（3）计算单元的应力
function stress = Bar2D2Node_Stress(E,x1,y1,x2,y2,alpha,u)
% 该函数计算单元的应力
% 输入弹性模量E，第一个结点的坐标（x1,y1）,第二个节点的坐标（x2,y2）
% 输入角度（alpha），单位结点位移矢量u
% 返回单元应力标量stress
L= sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
x = alpha*pi/180;
C=cos(x);
S=sin(x);
stress = E/L*[-C -S C S]*u;
end
解答步骤
(1)结构的离散化和编号
对结点和杆单元进行编号，如上图所示。
>> E = 2.95e11;
>> A = 0.0001;
>> x1=0;
>> y1=0;
>> x2=0.4;
>> y2=0;
>> x3=0.4;
>> y3=0.3;
>> x4=0;
>> y4=0.3;
>> alpha1=0;
>> alpha2=90;
>> alpha3=atan(0.75)*180/pi;
（2）计算各单元的刚度矩阵
对比弹簧单元和杆单元可以得到
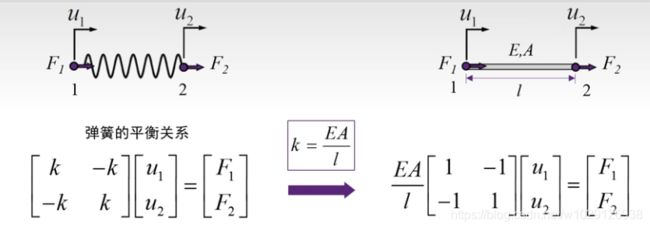k是弹簧的弹性系数，E是杆单元的弹性模量，A是横截面积，l是长度
利用Bar2D2Node_Stiffness函数分别对杆单元1，2，3，4计算其刚度矩阵。
>> k1 = Bar2D2Node_Stiffness(E,A,x1,y1,x2,y2,alpha1)
k1 =
73750000 0 -73750000 0
0 0 0 0
-73750000 0 73750000 0
0 0 0 0
>> k2 = Bar2D2Node_Stiffness(E,A,x2,y2,x3,y3,alpha2)
k2 =
1.0e+07 *
0.0000 0.0000 -0.0000 -0.0000
0.0000 9.8333 -0.0000 -9.8333
-0.0000 -0.0000 0.0000 0.0000
-0.0000 -9.8333 0.0000 9.8333
>> k3 = Bar2D2Node_Stiffness(E,A,x1,y1,x3,y3,alpha3)
k3 =
1.0e+07 *
3.7760 2.8320 -3.7760 -2.8320
2.8320 2.1240 -2.8320 -2.1240
-3.7760 -2.8320 3.7760 2.8320
-2.8320 -2.1240 2.8320 2.1240
>> k4 = Bar2D2Node_Stiffness(E,A,x4,y4,x3,y3,alpha1)
k4 =
73750000 0 -73750000 0
0 0 0 0
-73750000 0 73750000 0
0 0 0 0
（3）建立整体的刚度方程
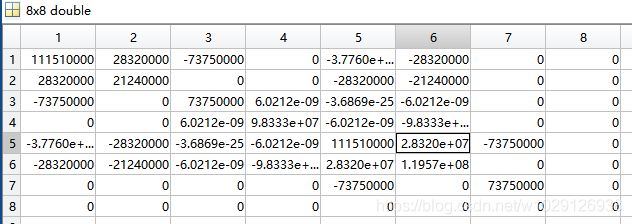
由于该结构有四个节点，每个节点各有x，y两个方向的自由度，因此，设整体的刚度矩阵为KK（8×8），先对KK清零，后调用Bar2D2Node_Assembly函数进行刚度矩阵的组装。
>> KK = zeros(8,8);
>> KK = Bar2D2Node_Assembly(KK,k1,1,2);
>> KK = Bar2D2Node_Assembly(KK,k2,2,3);
>> KK = Bar2D2Node_Assembly(KK,k3,1,3);
>> KK = Bar2D2Node_Assembly(KK,k4,4,3);
KK长这个样
（4）边界条件处理及刚度方程求解（求各个节点的位移）
实际上就是把不动的节点的行和列划掉。
节点1在x和y方向上不动，节点2只在x方向上移动，节点3在x和y方向上都有位移，节点4在x和y方向上不动。因此最后得到的位移矩阵就是3×3的刚度矩阵。再将节点力带入，可得到位移矩阵。
>> k = KK([3,5,6],[3,5,6])
k =
1.0e+08 *
0.7375 -0.0000 -0.0000
-0.0000 1.1151 0.2832
-0.0000 0.2832 1.1957
>> p=[20000;0;-25000];
>> u = k\p
u =
1.0e-03 *
0.2712
0.0565
-0.2225
>>
其中u是位移矩阵
（5）支反力的计算
首先把总的结点位移列出来，将总的结点位移乘上总的刚度矩阵得到所有结点里的结果，这个结果包含外部力和支反力。
>> q = [0 0 0.0002712 0 0.0000565 -0.0002225 0 0]'
q =
1.0e-03 *
0
0
0.2712
0
0.0565
-0.2225
0
0
>> P =KK*q
P =
1.0e+04 *
-1.5833
0.3126
2.0001
2.1879
-0.0001
-2.5005
-0.4167
0
>>
以上内容源自《有限元分析及应用》清华大学 曾攀老师主讲