怎样判断平面上一个矩形和一个圆形是否有重叠？

设 c为矩形中心， h为矩形半長， p为圆心，r为半径。

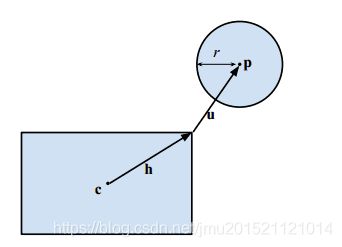
方法是计算圆心与矩形的最短距离 u，若 u 的长度小于 r 则两者相交。

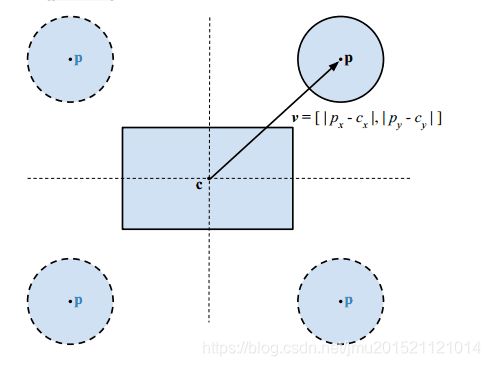
1. 首先利用绝对值把 p - c 转移到第一象限，下图显示不同象限的圆心也能映射至第一象限，这不影响相交测试的结果：

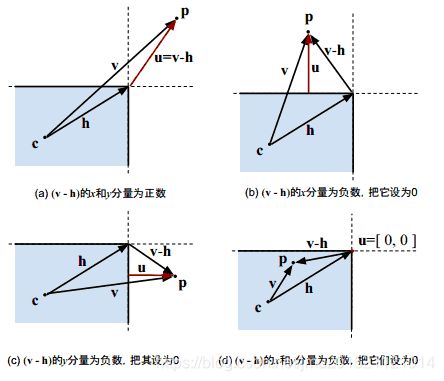
2. 然后，把 v 减去 h，负数的分量设置为0，就得到圆心与矩形最短距离的矢量 u。下图展示了4种情况，红色的 u是结果。

3. 最后要比较 u 和 r 的长度，若距离少于 r，则两者相交。可以只求 u 的长度平方是否小于 r 的平方。

代码：

bool BoxCircleIntersect(Vector2 c, Vector2 h, Vector2 p, float r) {
    Vector2 v = abs(p - c);    // 第1步：转换至第1象限
    Vector2 u = max(v - h, 0); // 第2步：求圆心至矩形的最短距离矢量
    return dot(u, u) <= r * r; // 第3步：长度平方与半径平方比较
} 

这个方法可能最早记录于[1]，而[2][3]也有相关描述。这个方法应该是最优的，而且可扩展至任何维度。如矩形不是轴对齐矩形（AABB）而是定向矩形（OBB），可以把圆心旋转至矩形的座标系。

这个方法考虑了矩形的对称及轴对齐性质，实际上等同5个分离轴测试[3]，包括矩形4边、圆心与矩形最近点的分离轴。后者容易被忽略。

这类型问题可以使用 閔可夫斯基和转化为圆角矩形和点的相交问题，可以应用不同的距离函数，如[5]。

[1] Arvo, “A Simple Method for Box-Sphere Intersection Testing”, Graphics Gems, pp. 247-250, 1993. http://tog.acm.org/resources/GraphicsGems/gems/BoxSphere.c
[2] Gottschalk, "Separating axis theorem ",. Technical Report TR96-024, Department of Computer Science, UNC Chapel Hill, 1996.
[3] Philip, Eberly, Geometric tools for computer graphics , Morgan Kaufmann, pp.644-646, 2002.
[4] Gomez, “Simple Intersection Tests for Games,” Gamasutra, October 1999. Gamasutra - Simple Intersection Tests For Games
[5] Quilez, “Modeling with distance functions”, 2008. Iigo Quilez - fractals, computer graphics, mathematics, demoscene and more