吴恩达卷积神经网络学习笔记（二）

一.卷积神经网络（一）

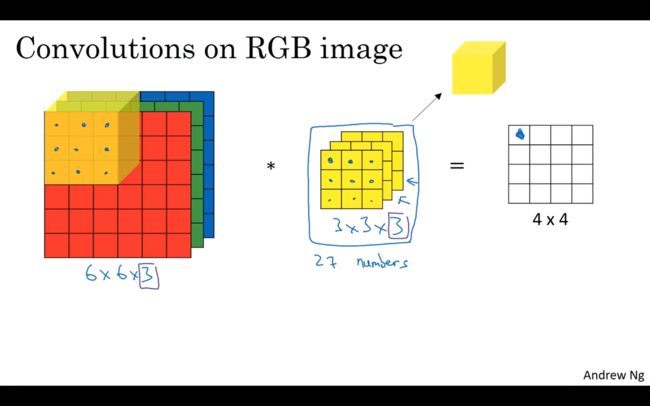
1.6 三维卷积

3指的是颜色通道（RGB） 

6*6*3分别对应宽*高*通道的数目

滤波器也有相对应的3*3*3，由此得到一个4*4的输出。

 对三维图像进行卷积时，卷积核的通道数要与三维图像的通道数相等。当我们想对图像的多个边缘特征进行检测时，我们可以使用多个卷积核，这样卷积后生成图像的通道数为使用的卷积核的个数。 

 对于三维卷积具体运算的实例如下：如果使用的是下图3*3*3的卷积核，则一共有27个参数，进行卷积运算时让数值与相应的参数相乘后求和，这就是最后4*4*1矩阵中的一个值。

第一个卷积核是垂直边缘检测，第二个是水平边缘检测器（利用两个不同的卷积核进行卷积，就会得到一个4*4*2的输出图层）

  （ nc是通道数目，前后两个都要相同。）

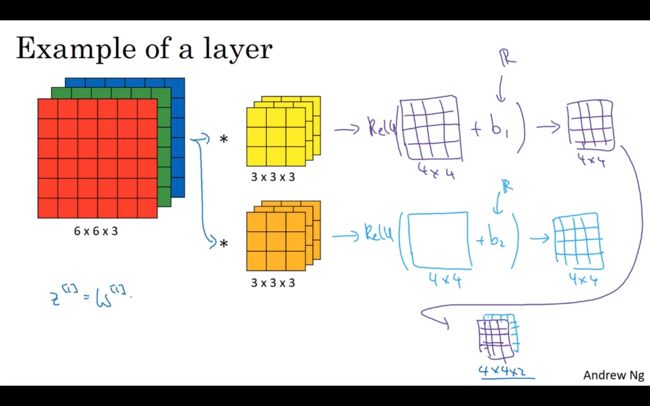
1.7 单层卷积网络

通过下图来说明卷积层所做的操作，但我们有一个6*6*3的图片输入时，我们想要提取图片的两个特征值，所以我们用了两个3*3*3的卷积核，然后对矩阵增添一个偏置量b（这是一个实数），通过Python的广播机制，给途中的16个元素都加上同一偏差，然后应用非线性函数，为了说明它是一个非线性激活函数ReLU，下一个如法炮制，把两个矩阵堆叠起来，从而生成了4*4*2的两个矩阵。

例如：3*3*3中，用10个滤波器，加一个偏差，则共有多少个参数值。共有（27+1)×10个参数

下图是对各个变量以及参数的维数的总结

f[l]:过滤器大小（也就是f*f）,,表示l层中过滤器大小为f*f;

f[l] = filter size

p[l] = padding

s[l] = stride

n_c[l] = number of filters

Each filter is: f[l] × f[l] × n_c[l]（如何得到通道数量）

Activations: a[l] —> n_h[l] × n_w[l] × n_c[l]

Weights: n_h[l] × n_w[l] × n_c[l] × n_c[l]

bias: n_c[l] —>(1,1,1,n_c[l])

input:n_h[l-1] × n_w[l-1] × n_c[l-1]

output:n_h[l] × n_w[l] × n_c[l]

n_h[l]=[(n_h[l-1] +2p[l] -f[l])/s[l] +1 ]

1.8 简单卷积网络示例

下图展示了使用一个卷积神经网络实现图片分类，在最后我们要将得到的矩阵展开成一个向量，然后输入到输出层的sigmoid函数或者softmax函数。对于卷积神经网络来说，通常图片会变小，通道数会增加。

解析：

nH[0]=nw=39，即高度和宽度都是39，0层的信道数量是3，假设第一层我们用一个3*3的数据集来提取特征，那么f[1]=3，因为是3*3的过滤器，s[1]=1,p[1]=0,所以高度和宽度都使用同一卷积。
如果有10个过滤器，神经网络下一层的激活值为37*37*10，（37是公式(（n+2p-f）/s)+1的计算结果），第一层标记为nH[1]=nW[1]=37,nC[1]=10,nC[1]等于第一层中过滤器的个数，这是第一层激活值的维度。
假设还有另外一个卷积层，这次采用的过滤器是5*5的矩阵，在标记发中，神经网络下一层的f=5,即f[2]=5，步幅为2，即s[2]=2,padding为0，即p[2]=0，其输出结果会是一张新图像，这次的输出结果是17*17*20，过滤器是20个，所以信道数量也是20 ，a[2]表示激活值维度，因此nH[2]=nW[2]=17，nC[2]=20。
最后图片提取了7*7*40=1960个特征
一个典型的卷积网络常有三层：卷积层、池化层、全连接层。

 
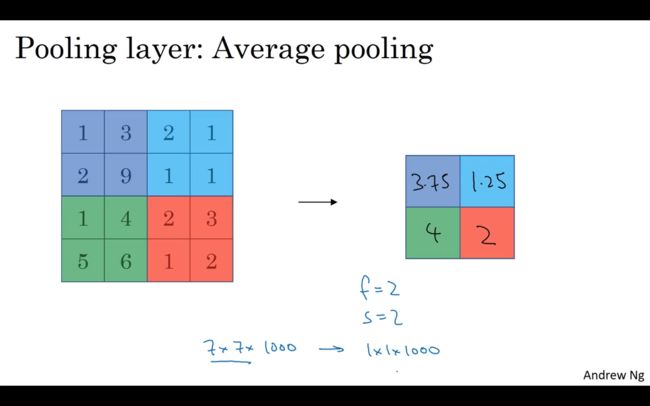
1.9 池化层

作用：利用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。

下图是最大池化，在每个作用区域内选择值最大的一个放在输出的方格上。当输入有多层时，对每一层都采用相同的操作，这样输入和输出的层数是相同的。最大池化的功能就是只要在任何一个象限内提取到某个特征，它都会保留在最大池化的输出里。最大池化运算的实际作用就是，如果在过滤器中提取到某个特征，那么保留其最大值，如果没有提取的这个特征，那么其最大值也是很小的。

  下图是平均池化，平均池化没有最大池化应用的广泛。

  需要注意的是，池化过程中的参数都是静态的，不需要进行学习，它只是一个静态属性。并且，卷积过程中计算维数的公式也可以应用在池化过程中。池化层的主要作用是特征降维，提高模型的鲁棒性。

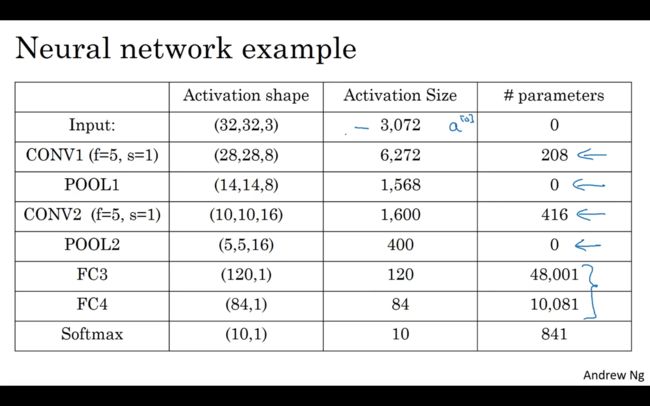
1.10 卷积神经网络示例

卷积神经网络一般将卷积层和池化层作为一层，为Layers,下图就是一个卷积神经网络的示例：

 随着神经网路的加深，激活值会逐渐变小，如果激活值下降太快，也会影响网络性能。

1.11   为什么使用卷积

与只使用全连接层相比，卷积层有两个优势：参数共享和稀疏连接。

 这样可以有效减少参数的数量。

 B站视频来源：【中英字幕】吴恩达深度学习课程第四课 — 卷积神经网络_哔哩哔哩_bilibili