三维重建（6）--多视图几何
目录
一、运动恢复问题（SfM）
二、欧式结构恢复问题
1、概述
2、算法流程
3、本质矩阵分解
4、欧式结构恢复歧义
三、仿射结构恢复问题
1、概述
2、因式分解法
3、仿射结构恢复歧义
四、透视结构恢复问题
1、概述
2、透视结构恢复歧义
3、代数方法
4、捆绑调整
五、P3P问题
六、随机采样一致性（RANSAC）
一、运动恢复问题（SfM）
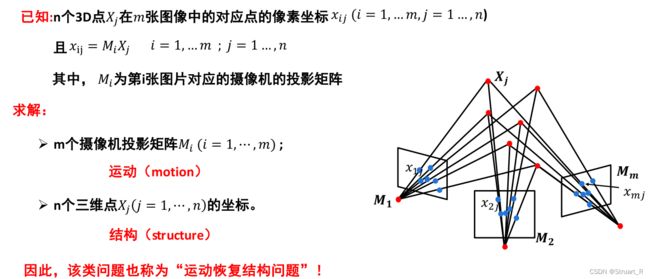
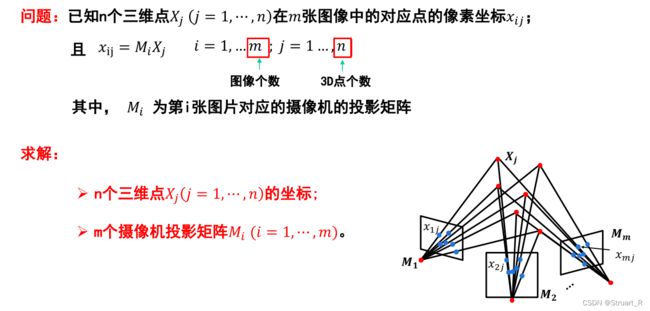
运动恢复问题：通过三维场景的多张图像，恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。
运动恢复问题建模表述：已知n个世界坐标点在m张图像中的对应点的像素坐标
，计算出m个摄像机的投影矩阵
和n个三维点
的坐标。
下图为求解SfM问题进行场景重构与计算摄像机位姿（投影矩阵得到的外参数）
二、欧式结构恢复问题
1、概述
欧式结构恢复问题：摄像机内参数已知，外参数未知情况。
对于欧式结构恢复问题，已知摄像机内参数，根据投影矩阵的计算公式可知，![x_{ij}=M_iX_j=K_i[R_i \hspace{0.25cm} T_i]X_j](http://img.e-com-net.com/image/info8/be6b075101864fc0997ac478968a43db.png){kind=small}
，其中
表示图像个数，
表示世界坐标下3D点个数，那么求解投影矩阵M只需要求解外参数![[R \hspace{0.25cm} T]](http://img.e-com-net.com/image/info8/c9efe13769d44378b365332a066b8d9d.png){kind=small}
。
2、算法流程
一般针对二视图问题的欧式结构重建问题，多视图即拆解为若干二视图问题。
对于二视图问题，外参数未知即表示摄像机1的外参数为![[I \hspace{0.25cm} 0]](http://img.e-com-net.com/image/info8/ec305e4f0e144b56bd60e099a1fce8fd.png){kind=small}
，而摄像机2的外参数为，即摄像机2与摄像机1的R、T关系为。
（1）求解基础矩阵F（归一化八点法）
（2）求解本质矩阵 
（3）分解本质矩阵 
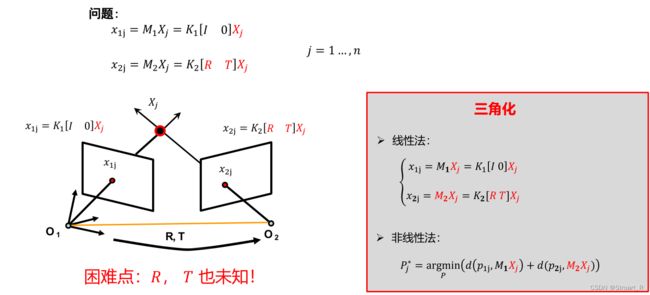
（4）三角化（求解世界坐标系下的3D坐标）
3、本质矩阵分解
算法流程中的第1,2,4步均已经提到过，所以此处不在介绍，详细过程请参见本专栏其他文章。
由于本质矩阵表达式为![E=T \times R=[T_x]R](http://img.e-com-net.com/image/info8/6ae20a9393e4437c8f89d2c4f802c93e.png){kind=small}
，这种叉乘关系一般都是通过奇异值分解的方式。另外，由于八点法求解的F的符号和尺度无法确定（本质上是
计算尺度的问题），所以E的符号和尺度也无法确定。
首先定义两个矩阵：
有性质成立：在相差一个正负号的情况下，
此时有![[T_x]=kUZU^T](http://img.e-com-net.com/image/info8/fbf3292fac404ad3972eaa0777f7aecc.png){kind=small}
成立，其中U是单位正交矩阵，这种结构可以用于后续的奇异值分解。
将W替换Z，且不考虑符号和尺度变化则：
![[T_x]=UZU^T \\ =Udiag(1,1,0)WU^T \\ =Udiag(1,1,0)W^TU^T](http://img.e-com-net.com/image/info8/25238e0a976a4dbba3260461b06b2692.png)
利用奇异值分解，由于本质矩阵E的秩为2，所以对角矩阵为
，则可分解为
，通过与上面的式子代换可得
，那么旋转矩阵R为下面表达式，两个解是由于不考虑尺度和符号的情况下。
通过奇异值分解，我们可以得到
是一个正交矩阵，从前面定义可以知道W是一个正交矩阵，则R为一个正交矩阵，满足旋转矩阵定义，另外需要保证行列式值为正，所以进一步完善R：
由于![T \times T=[T_x]T=UZU^TT=0](http://img.e-com-net.com/image/info8/733cf768c6134ec29dcc2945dd0e5489.png){kind=small}
(叉乘为0)，根据奇异值分解，
（U的第三列）。
这样本质矩阵分解的四个解就得到了，如何选择正确的那个解呢？只需要对多个点进行三角化，选择两个摄像机z坐标均为正最多的那组R、T，就是正确的解。
4、欧式结构恢复歧义
由于恢复的结构与真实场景之间相差一个相似变换（旋转、平移、缩放）。
三、仿射结构恢复问题
1、概述
仿射结构恢复问题：摄像机为仿射相机，内外参数均未知。
一般来说仿射相机代表为弱透视投影摄像机。
弱透视投影摄像机参见：三维重建（1）--摄像机几何-CSDN博客
下面图中所有坐标使用欧式坐标，对于仿射变换而言z轴的
，所以经过等式变换世界坐标的欧式坐标与像平面欧式坐标关系为
，其中
。
仿射结构恢复问题可以建模为：已知n个三维点在m张图像中的对应点的像素坐标为，且
，其中第i张图片对应的仿射相机的投影矩阵
，求解n个三维点的坐标以及m个仿射相机的投影矩阵中的
。
2、因式分解法
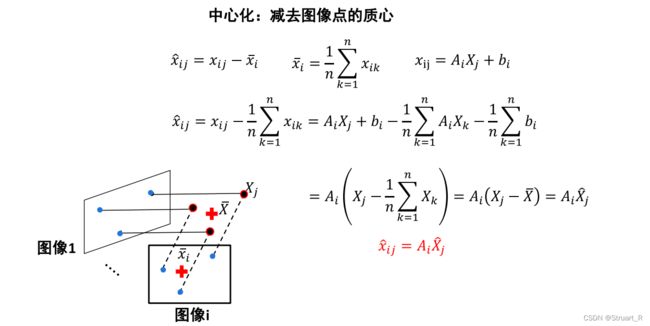
（1） 数据中心化
对于所有像平面点，和世界坐标的三维点分别减去像平面点和三维点的质心，建立新的关系，可知
，其中
，
。通过数据中心化消掉了b的影响。
通过上面的公式 ，我们可以将数据中心化矩阵形式写出，此时我们只需要解出下面M矩阵的值，所以也就是将
分解为
和
并得到M矩阵的值。
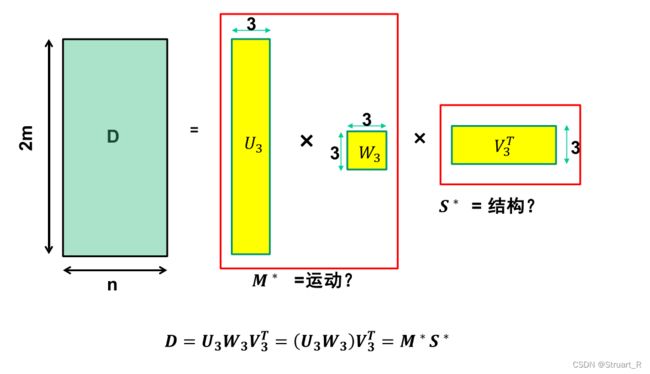
由于M和S的秩为3，所以D的秩为3，我们对矩阵进行奇异值分解，可以得到
，所以我们会得到新的2m*3的矩阵
，该矩阵与真实的参数A所构成的矩阵
之间差一个3*3的可逆矩阵H，这就是仿射结构的歧义。
3、仿射结构恢复歧义
仿射结构恢复歧义：投影矩阵存在一个可逆3*3矩阵的变换，也就是差了一个仿射变换的矩阵系数。
对于歧义我们需要引入其他约束来解决歧义。
另外对于给定m个相机，n个3维点情况下，我们将有2mn个等式，8m+3n-8个未知量。
四、透视结构恢复问题
1、概述
透视结构恢复问题：摄像机为透视相机，内外参数均未知。
问题建模：已知n个三维点在m张图像中的对应点的像素坐标为，且
，其中为第i张图片对应的摄像机投影矩阵，求解n个三维点的坐标以及m个摄像机投影矩阵。
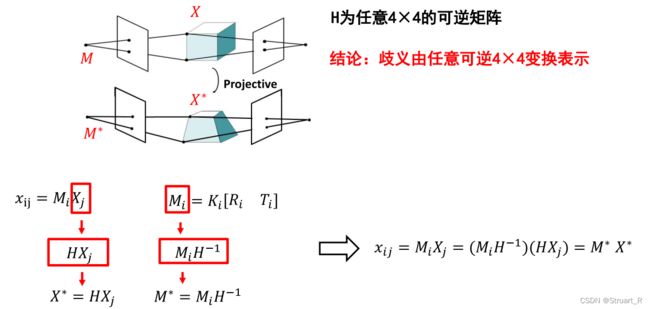
2、透视结构恢复歧义
透视结构与仿射结构的区别在于，透视结构计算得到的投影矩阵，与真实投影矩阵差一个4*4的可逆矩阵H，也就是差了一个透视变换关系。
对于给定m个相机，n个三维点，我们将有2mn个等式，11m+3n-15个未知量。
3、代数方法
下面的代数法基于二视图情况。多视图透视结构一般采用增量法。
算法流程：
（1）求解基础矩阵F（归一化八点法）
（2）基于F估计摄像机矩阵 
（3）三角化
对于第二步的解释：
对于透视结构的二视图问题，可以推导出基础矩阵F与A和b的关系：![F=[b_x]A](http://img.e-com-net.com/image/info8/9252fc211ff74a9a9affe823118f1bfe.png){kind=small}
。
如何计算A和b：
4、捆绑调整
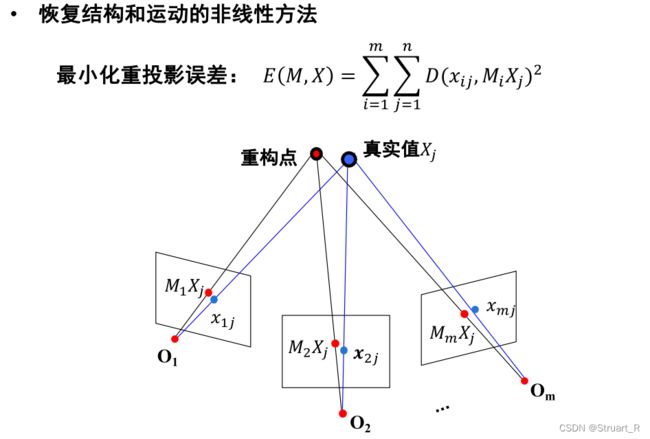
捆绑调整（Bundle Adjustment，BA），捆绑调整使用最小化重投影误差，可以进行多次迭代，使重构点足够拟合真实值，可以应用于欧式结构、仿射结构和透视结构多种情况，是一个恢复结构和运动的非线性方法。
代数法与分解法的局限性：
（1）因式分解法：假定所有点都是可见的，所以对于存在遮挡，建立对应点关系失败的情况将不得不删除该对应点关系。
（2）代数法：应用于2视图重建，容易出现误差累积。
最小化重投影误差：
利用最小化重投影误差，来计算投影矩阵，对于非线性最小化问题，可采用牛顿法和L-M法。
捆绑调整的优势：同时处理大量视图，处理丢失的数据
局限性：大量参数的最小化问题，需要良好的初始条件（即初始）
一般来说，捆绑调整作为SfM的最后一步，首先通过分解或代数方法先求出优化问题的初始。
五、P3P问题
PnP问题：指通过世界中N个三维点坐标及其在图像中N个像点坐标，计算出相机或物体位姿的问题。
P3P问题：对于PnP问题，我们只讨论世界中3个三维点和图像中3个像点的关系，计算欧式结构恢复相机位姿的问题，也就是计算出摄像机的外参数R、T。
相比于之前求F+三角化得到摄像机外参数的方法，该方法误差更小。
步骤1的计算方法：由于![a=K[I \hspace{0.2cm} 0]P_a](http://img.e-com-net.com/image/info8/17739f04e9d74ea8a4c12c350bd23b15.png){kind=small}
，则![K^{-1}a=[I \hspace{0.2cm} 0]P_a](http://img.e-com-net.com/image/info8/fad1e5936951491f8b641b248d205628.png){kind=small}
，所极点到像点a的方向向量为：
，同理可以计算出
。
P3P问题解法：
六、随机采样一致性（RANSAC）
随机采样（Random sample consensus,RANSAC）:一种适用于数据受到异常值污染的模型拟合方法，通过选择随机均匀采样一定的点，估计模型参数，并输出模型分数最高的模型。
算法流程：
（1）随机均匀采样获取模型求解所需的最小子集
（2）适用该子集估计模型参数
（3）计算剩余样本与当前模型的一致性，统计满足当前模型的内点（在正确拟合模型上的点为内点，负样本点为外点）个数，作为当前模型分数
（4）按照设定次数重复（1）-（3）步，最终输出分数最高的模型
Reference：https://www.bilibili.com/video/BV1aU4y1T74j/?spm_id_from=333.999.0.0&vd_source=2152dec20715e478285cc87cc31201ed