【数据结构】极致详解:树与二叉树(下)——链式存储实现
目录
前言:
一、链式存储概述:
二、链式结构的遍历:
1.前序、中序与后序遍历:
2.层序遍历:
三、链式存储结构各接口功能实现:
1.创建二叉树结构:
2.创建二叉树节点:
3.前序遍历:
4.中序遍历:
5.后序遍历:
6.层序遍历:
7.二叉树元素个数:
8.叶节点个数:
9.第 K 层节点个数:
10.查找元素:
11.完全二叉树判断:
12.二叉树销毁:
四、链式存储结构完整代码:
1.Heap.h:
2.Heap.c:
总结:
️博客主页:✈️銮同学的干货分享基地
️欢迎关注:点赞收藏✍️留言
️系列专栏: 数据结构
【进阶】C语言学习
C语言学习
️代码仓库:数据结构仓库
VS2022_C语言仓库
家人们更新不易,你们的点赞和⭐关注⭐真的对我真重要,各位路过的友友麻烦多多点赞关注,欢迎你们的私信提问,感谢你们的转发!
关注我,关注我,关注我,你们将会看到更多的优质内容!!
本文重点 :
二叉树的链式存储结构实现
前言:
上节课我们学习了关于堆的应用,即 TOP-K 问题的解决方法,实现了各接口功能,同时标志着我们关于二叉树顺序存储结构的完美结束。而这节课我们就将继续研究二叉树的另一种存储结构,即二叉树链式存储结构的相关接口功能的实现。
一、链式存储概述:
前面我们说过,二叉树的存储结构一般可以简单地分为顺序存储结构与链式存储结构,今天我们将要进行研究的,就是其实中的链式存储结构。
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
链式存储结构又可以分为二叉链与三叉链:
我们今天要研究的,是其中的二叉链部分,而三叉链的讲解我们暂时不关心,将来在研究红黑树时,将会极尽细致的为各位小伙伴们进行讲解。
二、链式结构的遍历:
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是指:按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。同时,遍历也是二叉树上最重要的运算之一,是二叉树上进行其它运算的基础。
1.前序、中序与后序遍历:
按照规则,二叉树的遍历有:前序、中序与后序的递归结构遍历,其规则如下:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之间。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以 N(Node)、L(Left subtree)和 R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。
2.层序遍历:
除了最常用的先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为 1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第 2 层上的节点,接着是第三层的节点,以此类推。而这种自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
三、链式存储结构各接口功能实现:
包括本节课在内,若没有特殊强调,默认我们使用标准模块化开发格式进行代码书写。
1.创建二叉树结构:
- 在实现二叉树其他接口功能之前,我们首先创建一个二叉树节点的结构体类型,然后我们就可以通过根节点对这个二叉树进行操作。
typedef char BDataType; typedef struct BinaryTreeNode { struct BinaryTreeNode* left; // 指向当前节点左孩子 struct BinaryTreeNode* right; // 指向当前节点右孩子 BDataType data; // 当前节点值域 }BNode;
2.创建二叉树节点:
- 节点的创建只需要动态开辟一个空间,用于存放我们节点的值,再将左右指针置空,并返回创建好的节点的地址即可。
BNode* CreateTreeNode(BDataType x) { BNode* node = (BNode*)malloc(sizeof(BNode)); node->data = x; node->left = NULL; node->right = NULL; return node; }
3.前序遍历:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 对于前序遍历的操作原理,我们可以结合这张示意图来理解:
- 这个接口的实现方式(访问顺序)为:先访问根节点,即当前节点的值,接着递归访问左子树,最后递归访问右子树。
- 使用递归实现整个二叉树的遍历,而不使用循环语句。
void PrevOrder(BNode* root) { if (root == NULL) { printf("PrevOrder Error!\n"); return; } printf("%c ", root->data); // 访问当前节点的值 PrevOrder(root->left); // 先递归访问当前节点的左子树 PrevOrder(root->right); // 再递归访问当中前节点的右子树 }
4.中序遍历:
- 执行操作前需进行非空判断,防止对空指针进行操作。
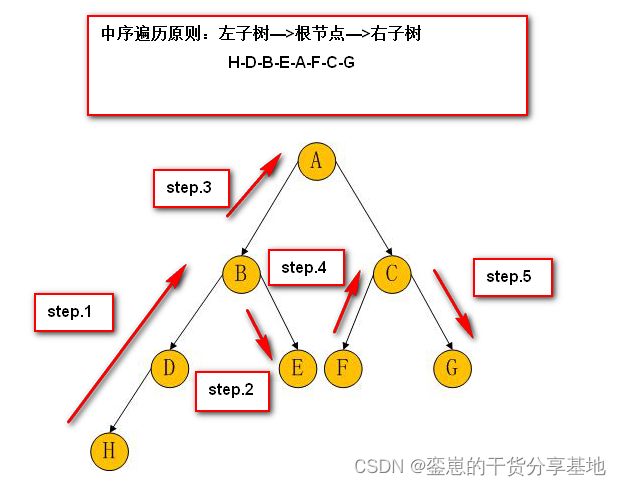
- 同样我们结合操作原理示意图来理解:
- 这个接口的实现方式(访问顺序)为:先递归访问左树,再访问节点自身,最后递归访问右树。
- 中序遍历同样使用递归实现整个二叉树的遍历,而不使用循环语句。
void InOrder(BNode* root) { if (root == NULL) { printf("InOrder Error!\n"); return; } InOrder(root->left); // 递归访问当前节点的左树 printf("%c ", root->data); // 访问当前节点的值 InOrder(root->right); // 最后递归访问当前节点的右树 }
5.后序遍历:
- 执行操作前需进行非空判断,防止对空指针进行操作。
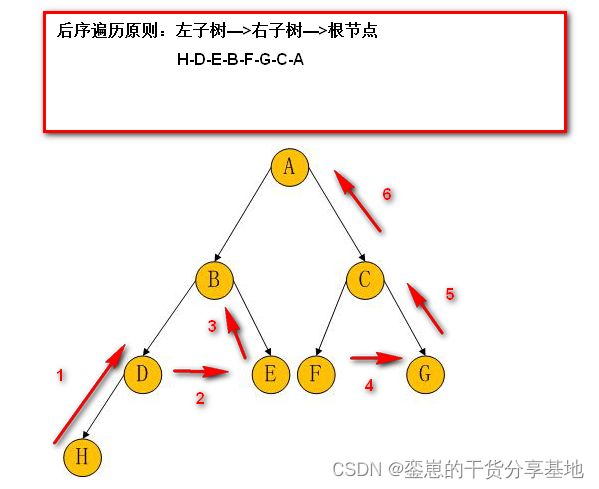
- 后序遍历操作原理示意图:
- 后序遍历接口的实现方式(访问顺序)为:先递归访问左子树,再递归访问右子树,最后访问节点自身。
- 后续遍历也使用递归实现整个二叉树的遍历,而不使用循环语句。
void PostOrder(BNode* root) { if (root == NULL) { printf("PostQrder Error!\n"); return; } PostOrder(root->left); // 先递归访问左子树 PostOrder(root->right); // 再递归访问右子树 printf("%c ", root->data); // 最后访问当前节点的值 }
6.层序遍历:
- 执行操作前需进行非空判断,防止对空指针进行操作。
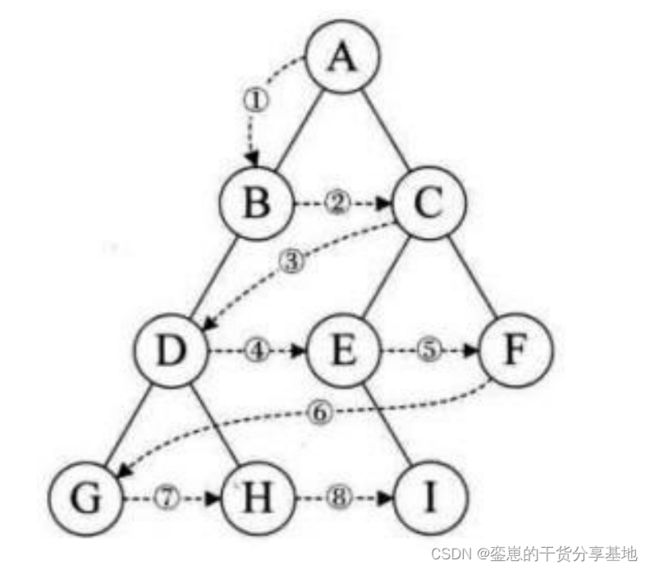
- 层序遍历操作原理示意图:
- 层序遍历就是一层一层的遍历,在链式储存中,我们一般借助队列来实现层序遍历。
- 利用的是队列的先进先出的性质。先让根入队,然后出队头数据,再让队头数据的左右孩子入队。每从队头删除掉一个元素,就让这个元素的两个孩子入队,直到队列为空为止。
- 首先创建队列,并对队列进行初始化。接着让二叉树的根入队(注意修改队列元素的类型)。判断队列是否为空,如果队列为空,说明遍历已经结束,应当换行并销毁队列。若队列不为空,就将队头的节点拷贝出来,然后删除队头节点,把拷贝的队头节点数据进行打印,最后让拷贝接节点的左右孩子先后入队。如果孩子没有子节点,相当于使空 NULL 入队,并不影响访问结果。
void TreeLevelOrder(BNode* root) { Q q; QInit(&q); if (root) { QPush(&q, root); } while (!QEmpty(&q)) { BNode* front = QFront(&q); QPop(&q); printf("%c ", front->data); if (front->left) { QPush(&q, front->left); } if (front->right) { QPush(&q, front->right); } } printf("\n"); QDestroy(&q); }
7.二叉树元素个数:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 对于二叉树元素(节点)数量的统计,我们采用的方式是任意选择一种遍历顺序(只依照遍历顺序,不访问节点),遍历整个树结构,每找到一个节点让计数变量加一即可:
void TreeSize(BNode* root, int* size) { if (root == NULL) { printf("TreeSize Get Error!\n"); return; } (*size)++; TreeSize(root->left, size); TreeSize(root->right, size); }
8.叶节点个数:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 叶节点就是度为0的节点,即没有子树,我们同样使用递归进行统计。
- 如果一个节点为空(结构内没有存放左右子节点),那它的叶节点个数肯定为 0;如果一个节点的左子树和右子树同时为空,说明这是一个叶节点。如果不是,其左子树的叶节点和右子树的叶节点之和就是当前节点以下的所以叶节点,形成递归。
- 根节点进入函数后,应当首先判断根节点是否为叶节点,如果不是就计算根节点左右子树的叶节点的和,形成递归。
int TreeLeafSize(BNode* root) { if (root == NULL) { printf("TreeLeafSize Get Error!\n"); return 0; } else { return (root->left) == NULL && (root->right) == NULL ? 1 : TreeLeafSize(root->left) + TreeLeafSize(root->right); } }
9.第 K 层节点个数:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 若根节点为空,则节点的个数为0。如果我们要计算第 K 层的元素(节点)个数,首先从根节点开始统计,假设我们每向下一层 K 就减 1,那么当 K = 1 时,表示我们来到了第 K 层,然后计算 K = 1 时的节点个数返回值相加的结果即可。
int TreeKLevelSize(BNode* root, int k) { if (root == NULL) { printf("TreeKLevelSize Get Error!\n"); return 0; } if (k == 1) { return 1; } return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1); }
10.查找元素:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 若节点为空,就返回空。若节点的值等于要查找的值,就返回节点的坐标。
- 若节点不为空,但节点的值不是我们要查找的值,就查找节点的左子树,如果查找的结果不为空,就返回该节点。若左子树的查找结果为空,就以同样的方式处理右子树。如果都找不到,就返回空。
BNode* TreeFind(BNode* root, BDataType x) { if (root == NULL) { return NULL; } if (root->data == x) { return root; } BNode* lret = TreeFind(root->left, x); if (lret) { return lret; } BNode* rret = TreeFind(root->right, x); if (rret) { return rret; } return NULL; }
11.完全二叉树判断:
- 执行操作前需进行非空判断,防止对空指针进行操作。
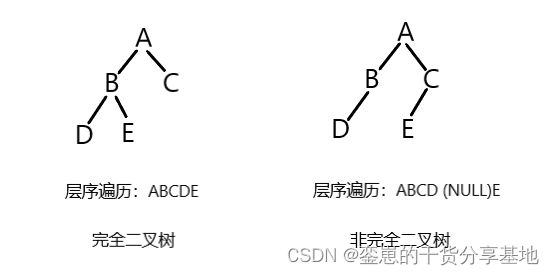
- 判断原理示意图:
- 若一个二叉树不是完全二叉树时,那么当我们对它进行层序遍历时,其中的部分节点就会是 NULL,于是我们可以通过这一点来判断一个二叉树是否为完全二叉树。
- 前半部分与二叉树的层序遍历一样,建队列,根入队,队列不为空,进入while循环,在循环中删队头节点,然后让该节点的左右孩子入队。要特别注意的是,这里循环停止的条件还要加上一个即堆顶的元素为空。在跳出循环后存在两种情况,第一种是队列已空,节点之间没有空,表明是完全二叉树,返回true;而第二种情况是队列不为空,但在访问队头节点时访问到了 NULL,这时我们需要再次进行循环,若队列不为空,就进入循环逐个查找并删除队头的节点,若发现不为空的节点,说明节点间有 NULL 相隔,即该二叉树不是完全二叉树,返回false。
bool BinaryTreeComplete(BNode* root) { Q q; QInit(&q); if (root) { QPush(&q, root); } while (!QEmpty(&q)) { BNode* front = QFront(&q); QPop(&q); if (front == NULL) { break; } QPush(&q, front->left); QPush(&q, front->right); } while (!QEmpty(&q)) { BNode* front = QFront(&q); QPop(&q); if (front) { return false; } } QDestroy(&q); return true; }
12.二叉树销毁:
- 执行操作前需进行非空判断,防止对空指针进行操作。
- 销毁二叉树需要把二叉树的每个节点都销毁,故采用后序遍历的顺序进行销毁。
- 注意:节点里存放的是左右孩子的指针,若我们在传参时仅传递节点的指针类型,则函数中的左右孩子地址就是一份临时拷贝,将导致无法对每个节点的指针进行置空,故我们在销毁二叉树时,函数参数应当传递二级指针。
void BinaryTreeDestory(BNode** pproot) { if (*pproot == NULL) { printf("BinaryTreeDestroy Error!\n"); return NULL; } BinaryTreeDestory(&(*pproot)->left); BinaryTreeDestory(&(*pproot)->right); free(*pproot); pproot = NULL; }
四、链式存储结构完整代码:
1.Heap.h:
#pragma once
#include
#include
#include
#include
//队列(为层序遍历做准备):
typedef int QDataType;
typedef struct QueueNode
{
QDataType data;
struct QNode* next;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
}Q;
void QInit(Q* p); //初始化队列
void QPush(Q* p, QDataType x); //入队
void QPop(Q* p); //出队
QDataType QFront(Q* p); //查看队头
bool QEmpty(Q* p); //查看队列容量
void QDestroy(Q* p); //队列的销毁
//二叉树的链式结构:
typedef char BDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left; // 指向当前节点左孩子
struct BinaryTreeNode* right; // 指向当前节点右孩子
BDataType data; // 当前节点值域
}BNode;
BNode* CreateTreeNode(BDataType x); //二叉树节点创建
void PrevOrder(BNode* root); // 前序遍历
void InOrder(BNode* root); // 中序遍历
void PostOrder(BNode* root); // 后序遍历
void TreeLevelOrder(BNode* root); //层序遍历
void TreeSize(BNode* root, int* size); // 统计二叉树元素个数
int TreeLeafSize(BNode* root); // 计算叶节点个数
int TreeKLevelSize(BNode* root, int k); // 计算第 K 层的节点个数
BNode* TreeFind(BNode* root, BDataType x); // 查找元素(节点)
bool BinaryTreeComplete(BNode* root); // 完全二叉树判断 2.Heap.c:
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
//队列部分接口(为层序遍历做准备):
//初始化队列
void QInit(Q* p)
{
if (p == NULL)
{
printf("QueueINit fail\n");
return;
}
p->head = NULL;
p->tail = NULL;
}
//入队:
void QPush(Q* p, QDataType x)
{
if (p == NULL)
{
printf("QueuePush fail\n");
return;
}
//申请新节点:
QNode* newnode = (QNode*)malloc(sizeof(QNode));
newnode->data = x;
newnode->next = NULL;
//分情况插入:
if (p->head == NULL)
{
p->head = p->tail = newnode;
}
else
{
//将新节点连接在队尾:
p->tail->next = newnode;
//更新队尾:
p->tail = newnode;
}
}
//出队:
void QPop(Q* p)
{
if (p == NULL)
{
printf("QueuePop fail\n");
exit;
}
if (QEMpty(p))
{
printf("Queue is NUll\n");
return;
}
else
{
QNode* next = p->head->next; //记录第二数据
free(p->head); //释放原头节点
p->head = next; //更新头节点
//注意对删空队列的情况应进行区分处理
if (p->head == NULL)
{
p->tail = NULL;
}
}
}
//查看队头
QDataType QFront(Q* p)
{
if (p == NULL)
{
printf("QueueFront get fail\n");
return;
}
if (QEmpty(p))
{
printf("The Queue is NULl\n");
return;
}
return p->head->data;
}
//查看队列容量
bool QEmpty(Q* p)
{
if (p == NULL)
{
printf("QueueEmpty fail\n");
return;
}
return p->head == NULL;
}
//队列的销毁:
void QDestroy(Q* p)
{
if (p == NULL)
{
printf("QueueNodeDestroy fail\n");
exit;
}
QNode* cur = p->head;
while (cur != NULL)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
p->head = p->tail = NULL;
}
//二叉树节点创建:
BNode* CreateTreeNode(BDataType x)
{
BNode* node = (BNode*)malloc(sizeof(BNode));
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
//前序遍历:
void PrevOrder(BNode* root)
{
if (root == NULL)
{
printf("PrevOrder Error!\n");
return;
}
printf("%c ", root->data); // 访问当前节点的值
PrevOrder(root->left); // 先递归访问当前节点的左子树
PrevOrder(root->right); // 再递归访问当中前节点的右子树
}
//中序遍历:
void InOrder(BNode* root)
{
if (root == NULL)
{
printf("InOrder Error!\n");
return;
}
InOrder(root->left); // 递归访问当前节点的左树
printf("%c ", root->data); // 访问当前节点的值
InOrder(root->right); // 最后递归访问当前节点的右树
}
//后序遍历:
void PostOrder(BNode* root)
{
if (root == NULL)
{
printf("PostQrder Error!\n");
return;
}
PostOrder(root->left); // 先递归访问左子树
PostOrder(root->right); // 再递归访问右子树
printf("%c ", root->data); // 最后访问当前节点的值
}
//层序遍历:
void TreeLevelOrder(BNode* root)
{
Q q;
QInit(&q);
if (root)
{
QPush(&q, root);
}
while (!QEmpty(&q))
{
BNode* front = QFront(&q);
QPop(&q);
printf("%c ", front->data);
if (front->left)
{
QPush(&q, front->left);
}
if (front->right)
{
QPush(&q, front->right);
}
}
printf("\n");
QDestroy(&q);
}
//统计二叉树元素个数:
void TreeSize(BNode* root, int* size)
{
if (root == NULL)
{
printf("TreeSize Get Error!\n");
return;
}
(*size)++;
TreeSize(root->left, size);
TreeSize(root->right, size);
}
//计算叶节点个数:
int TreeLeafSize(BNode* root)
{
if (root == NULL)
{
printf("TreeLeafSize Get Error!\n");
return 0;
}
else
{
return (root->left) == NULL && (root->right) == NULL ? 1 : TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
}
//计算第 K 层的节点个数:
int TreeKLevelSize(BNode* root, int k)
{
if (root == NULL)
{
printf("TreeKLevelSize Get Error!\n");
return 0;
}
if (k == 1)
{
return 1;
}
return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}
//查找元素(节点):
BNode* TreeFind(BNode* root, BDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BNode* lret = TreeFind(root->left, x);
if (lret)
{
return lret;
}
BNode* rret = TreeFind(root->right, x);
if (rret)
{
return rret;
}
return NULL;
}
//完全二叉树判断:
bool BinaryTreeComplete(BNode* root)
{
Q q;
QInit(&q);
if (root)
{
QPush(&q, root);
}
while (!QEmpty(&q))
{
BNode* front = QFront(&q);
QPop(&q);
if (front == NULL)
{
break;
}
QPush(&q, front->left);
QPush(&q, front->right);
}
while (!QEmpty(&q))
{
BNode* front = QFront(&q);
QPop(&q);
if (front)
{
return false;
}
}
QDestroy(&q);
return true;
}
//二叉树销毁:
void BinaryTreeDestory(BNode** pproot)
{
if (*pproot == NULL)
{
printf("BinaryTreeDestroy Error!\n");
return NULL;
}
BinaryTreeDestory(&(*pproot)->left);
BinaryTreeDestory(&(*pproot)->right);
free(*pproot);
pproot = NULL;
}总结:
到这里,我们关于树与二叉树,以及二叉树的两种存储结构的学习就全部结束了,这里的学习相对来说比较基础,如果各位小伙伴们已经感觉到些许吃力,最好能够将这几篇节课的学习内容多复习几遍,以巩固自己的基础,为将来的排序与红黑树等相关内容的学习做好准备。
道路一旦选定,就勇敢地走到底,决不回头
更新不易,辛苦各位小伙伴们动动小手,三连走一走 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!