【论文阅读笔记】Towards Universal Unsupervised Anomaly Detection in Medical Imaging
Towards Universal Unsupervised Anomaly Detection in Medical Imaging
arxiv,19 Jan 2024 【开源】
【核心思想】
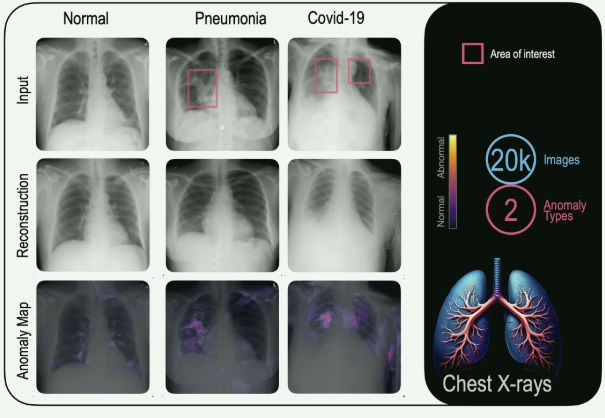
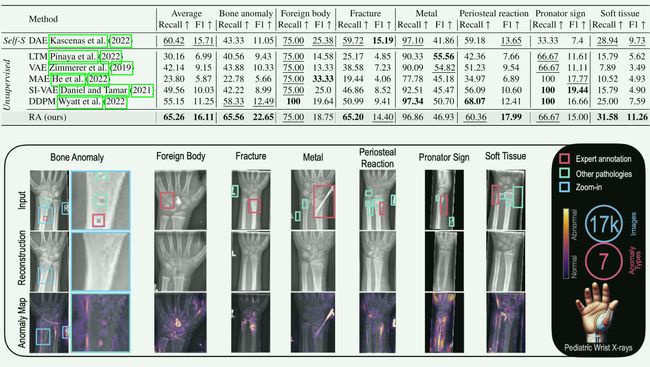
本文介绍了一种新的无监督异常检测方法—Reversed Auto-Encoders (RA),旨在提高医学影像中病理检测的准确性和范围。RA通过生成类似健康的重建图像,能够检测到更广泛的病理类型,这在现有技术中是一个挑战。RA方法在多种医学成像模态(如脑部磁共振成像、儿童腕部X光片和胸部X光片)中展示了卓越的检测性能,与现有最先进的方法相比,RA在检测各种病理、解剖结构和成像模态方面都表现出更高的准确性和稳健性。此外,RA的自动异常检测能力在缺乏放射学专业知识的环境中特别有价值。然而,该研究也指出了在检测极其微妙的异常方面的限制,强调了需要改进异常图计算和开发更为复杂的评估指标,以满足临床诊断的精细需求。总的来说,RA框架在医学成像领域展现出巨大潜力,其能够准确地检测广泛的异常,对于推动医学成像与人工智能的结合、提高诊断过程的准确性具有重要意义。
【医学影像中的异常检测的常用方法概述】
- 自监督方法:这些方法通过数据增强或预文本任务生成替代监督信号,利用数据固有特征和有限注释来识别异常。但这些方法可能会在预期的异常分布中引入偏见,尤其是当噪声或人工改变作为真实病理特征的代理时。例如,去噪自编码器(DAE)学习消除人工添加的粗糙高斯噪声,这种方法可能对特定异常(如脑肿瘤)有效,但对更广泛的异常检测应用有限。
- 无监督异常检测:无监督方法旨在从正常人群中学习标准分布,然后将这些知识应用于异常检测。传统的自编码器(AE)和变分自编码器(VAE)在此领域起到了基础性作用。AEs通过编码解码架构捕捉和重建输入数据,假设异常将表现为显著的重建错误。然而,AEs常常难以学习详细的正常解剖特征,并不适合泛化到病理。VAEs通过规范化潜在空间并将其视为概率分布来解决AE的一些局限性。这种规范化允许更受约束的学习过程,使VAEs能更紧密地遵循标准分布。然而,这种规范化经常导致重建的图像模糊,这在识别微妙异常时可能是一个缺点。
- 遮蔽自编码器(MAEs):这些方法也利用了先进的神经网络架构的优势,但从不同的角度来处理异常检测问题。MAEs通过选择性地遮蔽输入数据的部分,并让模型预测这些遮蔽部分来工作。
- 生成对抗网络(GANs):GANs引入了对抗性训练方法,能够生成高度真实的图像。然而,它们可能会遭受模式崩溃,或生成与输入数据不一致的图像。为解决这些挑战,像软内省变分自编码器(SI-VAEs)等进步技术已经出现,它们融合了VAEs和GANs,旨在克服GANs在异常检测中的特定局限性。
- 去噪扩散概率模型(DDPMs):DDPMs采用一种迭代方法,涉及在图像空间中添加和随后去除噪声。然而,DDPMs的一个关键方面在于精心选择噪声水平,这一决策极大地影响它们的性能。
【方法】
1.方法提出的背景
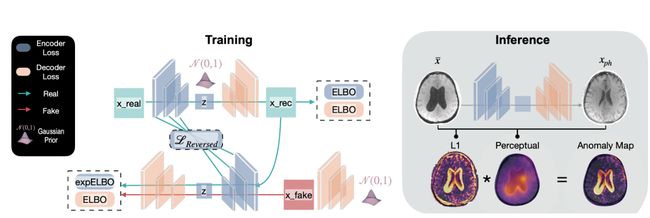
在训练阶段(左),使用多尺度反向嵌入损失 L Reversed \mathcal{L}_{\text {Reversed }} LReversed ,结合证据下界(ELBO)和对抗优化,对编码器和解码器网络进行优化。在此过程中,解码器从随机噪声中生成合成图像,目的是欺骗编码器将其视为真实图像 x fake x_{\text {fake }} xfake 。在推理阶段(右),RA模型处理一个新的输入 x x x ,将其编码并重建为伪健康图像 x p h x_{\mathrm{ph}} xph 。异常检测是通过计算 x x x和 x p h x_{\mathrm{ph}} xph 之间的 L1 范数和感知差异来进行的,从而得到突出显示病理区域的异常图。
将“正常”称为没有病理。给定一组正态样本 x ∈ X ⊂ R N x \in X \subset \mathbb{R}^{N} x∈X⊂RN ,AE的目标是找到函数 f : R N → R D f: \mathbb{R}^{N} \rightarrow \mathbb{R}^{D} f:RN→RD , g : R D → R N g: \mathbb{R}^{D} \rightarrow \mathbb{R}^{N} g:RD→RN 使得 x ≈ g ( f ( x ) ) x \approx g(f(x)) x≈g(f(x)) 。 f f f 分别 g g g 称为编码器和解码器,将 f f f 输入映射到较低维的表示形式。无监督异常检测(UAD)的基本假设是,这些学习的表示包含描述规范分布的特征,即使对于异常样本 x ˉ ∉ X \bar{x} \notin X xˉ∈/X 也是如此。因此, x p h = ( g ( f ( x ˉ ) ) ) ∈ X x_{p h}=(g(f(\bar{x}))) \in \mathcal{X} xph=(g(f(xˉ)))∈X 表示 x ˉ \bar x xˉ 的伪健康重建。异常分数通常来自输入与其重建之间的像素差异: s ( x ) = ∣ x − g ( f ( x ) ) ∣ s(x)=|x-g(f(x))| s(x)=∣x−g(f(x))∣ 。
在变分推理框架中,目标是通过最大化观测样本 x x x 的对数似然 log p θ ( x ) \log p_{\theta}(x) logpθ(x) 来优化潜在变量模型 ��(�) p θ ( x ) p_{\theta}(x) pθ(x) 的参数 θ \theta θ 。为了解决这个问题,真正的后验 p θ ( z ∣ x ) p_{\theta}(z \mid x) pθ(z∣x) 通过使用证据下限 (ELBO) 的提议分布 q ϕ ( z ∣ x ) q_{\phi}(z \mid x) qϕ(z∣x) 来近似: log p θ ( x ) ≥ E q ( z ∣ x ) [ log p θ ( x ∣ z ) ] − KL [ q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ] = ELBO ( x ) \log p_{\theta}(x) \geq \mathbb{E}_{q(z \mid x)}\left[\log p_{\theta}(x \mid z)\right]-\operatorname{KL}\left[q_{\phi}(z \mid x)|| p(z)\right]=\operatorname{ELBO}(x) logpθ(x)≥Eq(z∣x)[logpθ(x∣z)]−KL[qϕ(z∣x)∣∣p(z)]=ELBO(x)
p θ ( x ∣ z ) p_{\theta}(x \mid z) pθ(x∣z)和 q ϕ ( z ∣ x ) q_{\phi}(z \mid x) qϕ(z∣x)分别是解码器 D θ D_{\theta} Dθ和编码器 E ϕ E_{\phi} Eϕ,AE 通常使用正态分布作为先验分布 p ( z ) = N ( μ , σ ) p(z)=\mathcal{N}(\mu, \sigma) p(z)=N(μ,σ) ,并采用重参数化技巧来最大化 ELBO。为了将 VAE 的潜在特性与 GAN 的图像合成能力相结合,SI-VAE为 VAE 训练引入了对抗性损失。关键的创新是以对抗方式利用VAE的编码器和解码器,而无需外部鉴别器。该编码器旨在通过最小化真实样本和先验样本的潜在分布的KL散度来区分真实样本和生成样本,同时最大化生成样本的KL散度。相反,解码器通过使用标准ELBO重建真实数据样本并最小化编码器压缩的生成样本的KL散度来训练来“欺骗”编码器。编码器和解码器的优化目标如下:
L E ϕ ( x , z ) = ELBO ( x ) − 1 α ( exp ( α ELBO ( D θ ( z ) ) ) ) , L D θ ( x , z ) = ELBO ( x ) + γ ELBO ( D θ ( z ) ) , \begin{array}{l} \mathscr{L}_{E_{\phi}}(x, z)=\operatorname{ELBO}(x)-\frac{1}{\alpha}\left(\exp \left(\alpha \operatorname{ELBO}\left(D_{\theta}(z)\right)\right)\right), \\ \mathscr{L}_{D_{\theta}}(x, z)=\operatorname{ELBO}(x)+\gamma \operatorname{ELBO}\left(D_{\theta}(z)\right), \end{array} LEϕ(x,z)=ELBO(x)−α1(exp(αELBO(Dθ(z)))),LDθ(x,z)=ELBO(x)+γELBO(Dθ(z)),
2.RA: Reversed Autoencoders
RA的主要创新在于其复杂的训练机制,旨在学习和准确重建正常的解剖模式。通过三种不同训练策略的独特组合来实现:首先,利用ELBO对平滑潜在空间进行正则化处理,使模型能够有效地捕捉正常解剖特征的潜在分布;其次,实现了RA的编码器和解码器组件之间的内省对抗相互作用。这种相互作用确保了规范分布的高保真表示的生成,因为编码器和解码器相互挑战以优化其输出。最后,为了增强输入与其重建之间的连贯性——这在可能发生重大分歧的恢复阶段尤其重要——我们引入了“反向损失”。该损失函数旨在最大限度地减少原始图像与其重建版本之间的差异,从而确保 RA 在重建正常解剖结构时保持高度准确性,同时突出显示异常。
- Reversed Embedding Similarity
在编码器中实现反向多尺度嵌入相似性损失。这种方法确保输入表示与其生成的重建的嵌入紧密对齐,在多个尺度上执行:
L Reversed ( x ) = ∑ l = 0 L [ ( 1 − L Sim ( E ϕ l ( x ) , E ϕ l ( x rec ) ) ) + 1 2 MSE ( E ϕ l ( x ) , E ϕ l ( x rec ) ) ] , \begin{array}{r} \mathcal{L}_{\text {Reversed }}(x)=\sum_{l=0}^{L}\left[\left(1-\mathcal{L}_{\text {Sim }}\left(E_{\phi}^{l}(x), E_{\phi}^{l}\left(x_{\text {rec }}\right)\right)\right)\right. \\ \left.+\frac{1}{2} \operatorname{MSE}\left(E_{\phi}^{l}(x), E_{\phi}^{l}\left(x_{\text {rec }}\right)\right)\right], \end{array} LReversed (x)=∑l=0L[(1−LSim (Eϕl(x),Eϕl(xrec )))+21MSE(Eϕl(x),Eϕl(xrec ))],
其中 E ϕ l E_{\phi}^{l} Eϕl 表示 L L L 个编码器层的第 l l l 个嵌入, x rec = D θ ( E ϕ ( x ) ) , L Sim x_{\text {rec }}=D_{\theta}\left(E_{\phi}(x)\right), \mathcal{L}_{\text {Sim }} xrec =Dθ(Eϕ(x)),LSim 是余弦相似度, M S E MSE MSE 是均方误差。编码器的目标函数结合了反向相似性的概念,定义为:
L E ϕ ( x , z ) = ELBO ( x ) − 1 α ( exp ( α ELBO ( D θ ( z ) ) ) + λ L Reversed ( x ) \mathcal{L}_{E_{\phi}}(x, z)=\operatorname{ELBO}(x)-\frac{1}{\alpha}\left(\exp \left(\alpha \operatorname{ELBO}\left(D_{\theta}(z)\right)\right)+\lambda \mathcal{L}_{\text {Reversed }}(x)\right. LEϕ(x,z)=ELBO(x)−α1(exp(αELBO(Dθ(z)))+λLReversed (x)
-
异常分数计算
除了重建之外,准确检测异常还需要强大的异常评分计算方法。传统的基于残差的方法由于依赖于强度差异而经常面临局限性。为了解决这个问题,在计算残差之前应用自适应直方图均衡 。此外,还整合了感知差异,以增强异常检测的鲁棒性: s ( x ) = ∣ e q ( x p h ) − e q ( x ˉ ) ∣ × ( S lpips ( x p h , x ˉ ) × S lpips ( e q ( x p h ) , e q ( x ˉ ) ) ) s(x)=\left|\mathrm{eq}\left(x_{p h}\right)-\mathrm{eq}(\bar{x})\right| \times\left(\mathcal{S}_{\text {lpips }}\left(x_{p h}, \bar{x}\right) \times \mathcal{S}_{\text {lpips }}\left(\mathrm{eq}\left(x_{p h}\right), \mathrm{eq}(\bar{x})\right)\right) s(x)=∣eq(xph)−eq(xˉ)∣×(Slpips (xph,xˉ)×Slpips (eq(xph),eq(xˉ)))
其中 S lpips \mathcal{S}_{\text {lpips }} Slpips 表示学习的感知图像贴片相似度指标。
Perceptual Image Patch Similarity (PIPS)度量是一种用于评估图像之间相似性的方法,特别关注于感知特征。这种度量通常基于深度卷积神经网络(CNN)的特征,利用这些网络提取的特征来判断图像片段(patch)之间的相似度。PIPS度量的关键在于它不仅考虑像素级别的差异,而且还着眼于图像的感知特性,如结构和纹理。这使得PIPS度量能够更好地与人类视觉系统的感知一致,特别是在处理具有复杂纹理和结构的图像时。
【应用】