计算CNN卷积层和全连接层的参数量
计算CNN卷积层和全连接层的参数量
先前阅读
- CNN Explainer
- A Comprehensive Guide to Convolutional Neural Networks — the ELI5 way
本文主旨意在搞明白2个问题:
第一个问题
一个卷积操作,他的参数,也就是我们要训练的参数,也就是我们说的权重,有多少个? 看到一个nn.Conv()函数,就能知道有多少个,它由那些因子决定的?
参数量是由以下3个因子决定的:
- 卷积核大小(HxW)
- 卷积核维度(D)
- 卷积核有多少个
则卷积层的参数量为 卷积核大小(HxW) * 卷积核维度(D) * 卷积核有多少个
第二个问题
一个全连接操作,参数又有多少个?它由那些因子决定的?
- 输入大小为 N
- 输出大小为 M
则全连接层的参数量为 N×M
计算CNN卷积层的参数量
案例1
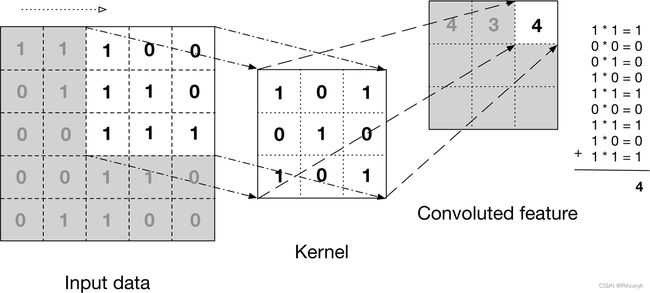
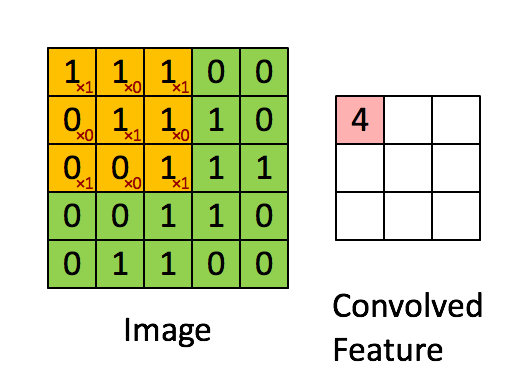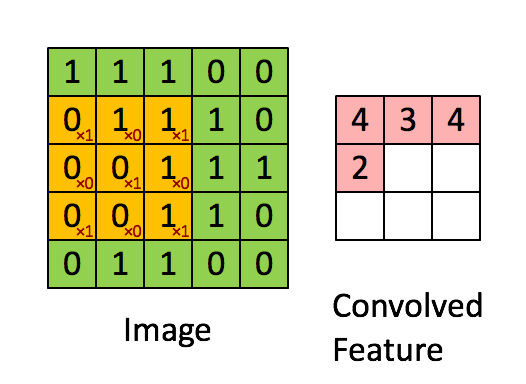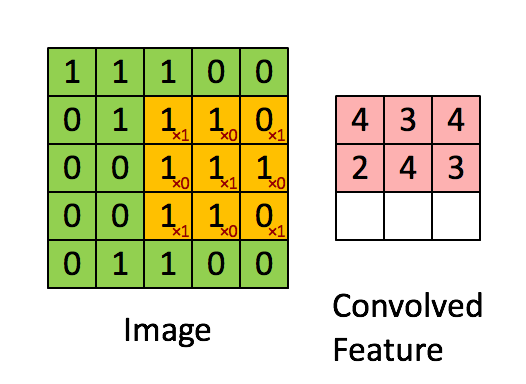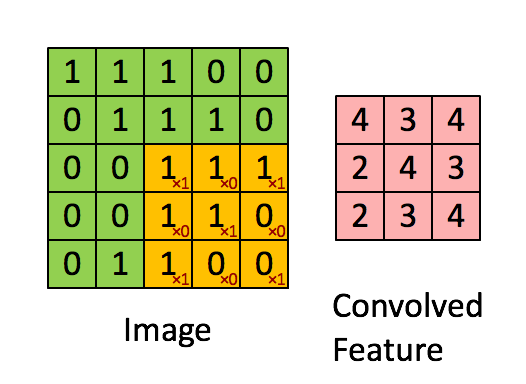
看上图案例1的计算,输入图像为 5x5x1, 卷积核3x3x1, 输出3x3x1;
思考3个参数:
- 卷积核大小(HxW) ==》3x3
- 卷积核维度(D) ==》1
- 卷积核有多少个 ==》1
参数量为 3x3x1x1 = 9个
案例2
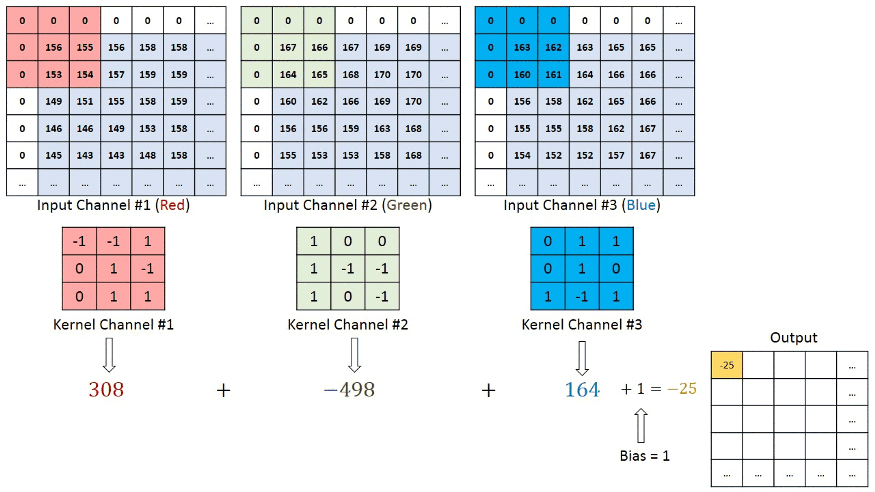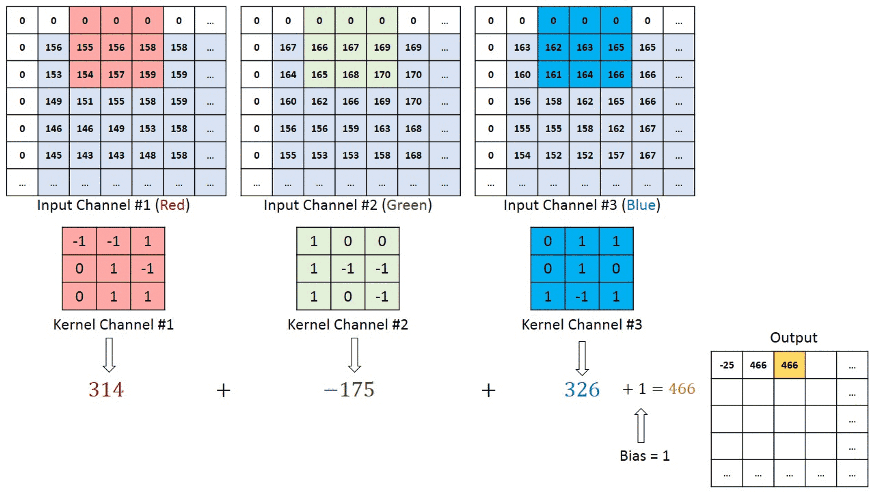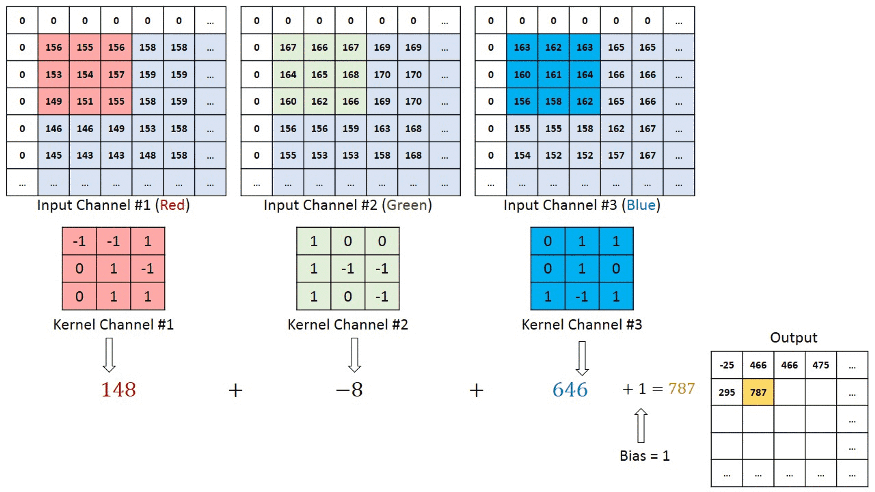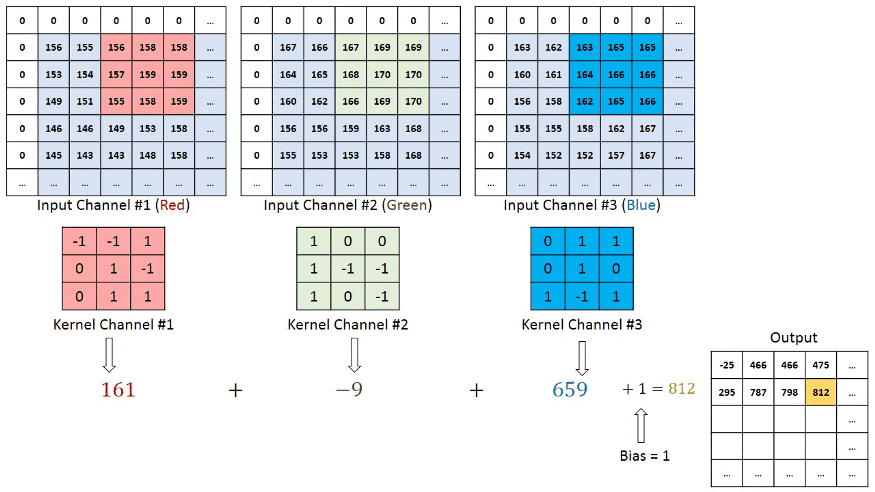
看上图案例2的计算,输入图像为 H1xW1x3, 卷积核3x3x3, 输出H2xW2x1;
思考3个参数:
- 卷积核大小(HxW) ==》3x3
- 卷积核维度(D) ==》3
- 卷积核有多少个 ==》1
参数量为 3x3x3x1 = 27个
从上面的两个案例可以看出, 参数量与输入图像的HxW没有关系, 参数量与输出图像的HxW也没有关系。
案例3
VGG-16为例,conv1-1,第一层
输入224x224x3, 输出是224x224x64,卷积核3x3
思考3个参数:
- 卷积核大小(HxW) ==》3x3
- 卷积核维度(D) ==》3
- 有多少个卷积核 ==》64
卷积核的维度是多少? 是由输入图像的维度决定,这里是3
卷积核的个数是多少? 是由输出图像的维度决定,这里是64
所以参数量 = 3x3x卷积核维度x卷积核个数 = 3x3x3x64 = 27个
Pytorch代码辅助理解
代码
nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
案例3中的卷积操作如下:
nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')
参数量计算: = kernel_size * kernel_size * in_channels(卷积核维度) * out_channels(卷积核个数) = 3 * 3 * 3 * 64
stride=1, padding=0, 这两个会影响到输出的HxW,上文已经提到和我们要计算的参数量无关。
最后,补上偏置参数,
每个卷积核都加个偏置 ,所以总得参数量:
参数量计算: = kernel_size * kernel_size * in_channels(卷积核维度) * out_channels(卷积核个数) + bias(=卷积核个数) = 3 * 3 * 3 * 64+64
计算FC全连接层的参数量
先看一段代码,这是我们经常看到的一段代码,先把x解析到1x9的维度,再做全连接操作
self.fc = nn.Linear(9, 4)
x = x.view(-1, 9) # 把x,解析到1x9的维度,这一个操作是没有权重的
x = self.fc(x) # 做全连接操作
上面的代码对应的操作图,如下

图片来源 | Fully Connected Layer vs. Convolutional Layer: Explained
红色框的参数,就是我们要找的权重参数,有多少个?
思考问题?
- 输入大小为 N = 9
- 输出大小为 M =4
计算参数量 = 9x4 = 36个
再看对应的连接图
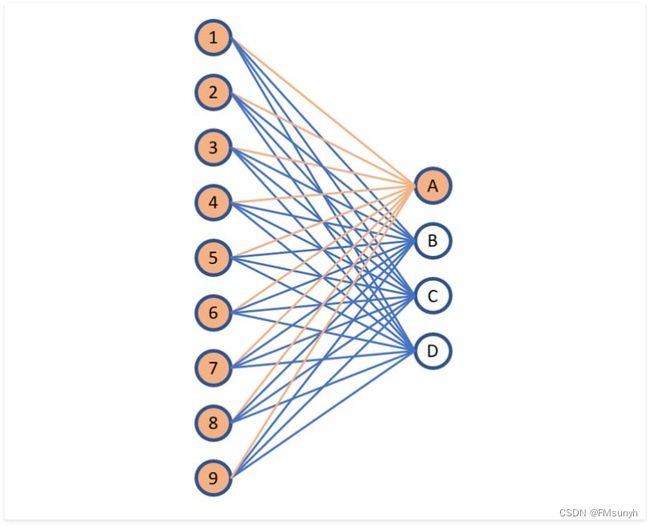
上图中的每一条连接线(橙色和蓝色的线),都有一个权重参数,共36条,所以有36个参数。
最后,补上偏置参数,
偏置参数数量: 每个输出节点有一个偏置项(bias),因此偏置参数的数量等于输出节点的数量,即 M=4
所以,总的参数数量为N×M+M = 40,即 M 为输出节点数量,N 为输入节点数量。
END