第十四届蓝桥杯省赛C++B组题目及解析

因为最近没有cf的比赛，于是在acwing摸鱼（不是，发现y总把去年蓝桥杯的题目搬过来了，正好借助这个机会进行补题。

第一题题目链接：4956. 冶炼金属 - AcWing题库

小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X

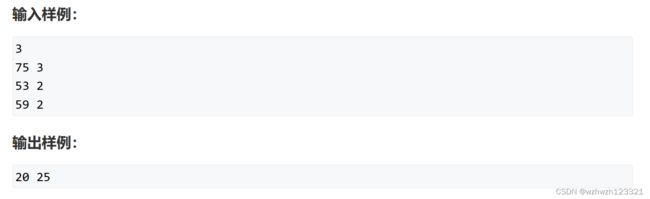
这个炉子有一个称作转换率的属性 V，V 是一个正整数，这意味着消耗 V 个普通金属 O 恰好可以冶炼出一个特殊金属 X，当普通金属 O 的数目不足 V时，无法继续冶炼。现在给出了 N条冶炼记录，每条记录中包含两个整数 A 和 B，这表示本次投入了 A 个普通金属 O，最终冶炼出了 B 个特殊金属 X。每条记录都是独立的，这意味着上一次没消耗完的普通金属 O不会累加到下一次的冶炼当中。根据这 N条冶炼记录，请你推测出转换率 V 的最小值和最大值分别可能是多少，题目保证评测数据不存在无解的情况。

最开始做的时候通过观察这个样例能够很容易发现通过数学公式似乎是可以做的，20是通过59+1除以2+1得出的最小值，25是通过75除以3得出的最大值，那么我们可以得到如下的数学公式

于是在第一遍做的过程中写下的代码如下：

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;

int maxx = 0x3f3f3f3f, minn;
int n;
const int N = 10010;
int a[N], b[N];


int main() {
	ios::sync_with_stdio(false);
	cin >> n;

	for (int i = 0; i < n; i ++) {

		cin >> a[i] >> b[i];

		if (a[i] / b[i] < maxx)
			maxx = a[i] / b[i];

		if ((a[i] + 1) / (b[i] + 1) > minn)
			minn = (a[i] + 1) / (b[i] + 1);
	}

	cout << minn << " " << maxx << endl;
	return 0;
}

运行后和样例非常匹配，本以为完美，没想到居然WA了

这个错误数据也挺离谱，于是根据这个样例简单修改，构造出了WA的数据，数据如下：

可以看出，答案不应该是20，如果是20那么就和60 2这个数据冲突了，思考后发现如果存在正好整除的这种情况那么不能简单的进行都加一后再做除法，或者说就算先进行了除法运算也需要最后再检查一下是否是整除的情况并根据是否发生了冲突进行修改，了解到错误原因后，修改如下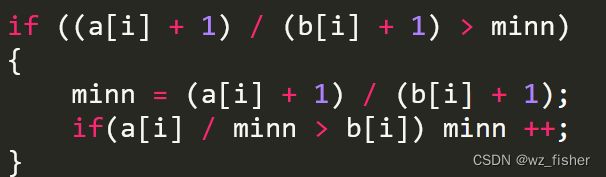

在minn取值后再通过一个if语句检查，如果不符合则minn加一，运行后AC

写在后面：不用数组存下来，用两个变量边读取边判断就行，做的时候没有考虑到，不过只要数据范围不离谱一般不会超过空间限制。

第二题题目链接：4957. 飞机降落 - AcWing题库

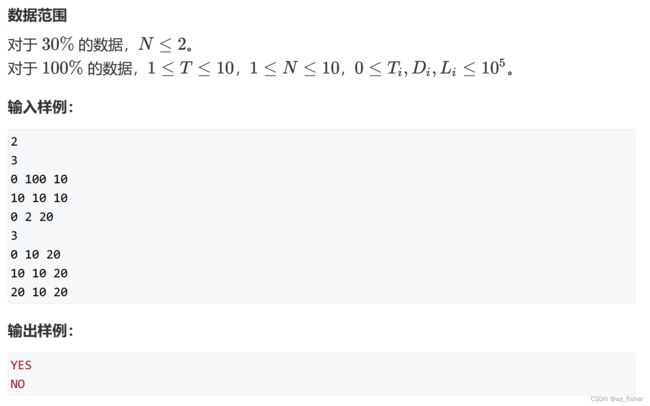
有 N架飞机准备降落到某个只有一条跑道的机场。

其中第 i架飞机在 Ti 时刻到达机场上空，到达时它的剩余油料还可以继续盘旋 Di 个单位时间，即它最早可以于 Ti 时刻开始降落，最晚可以于 Ti+Di时刻开始降落。降落过程需要 Li个单位时间。

一架飞机降落完毕时，另一架飞机可以立即在同一时刻开始降落，但是不能在前一架飞机完成降落前开始降落。

请你判断 N架飞机是否可以全部安全降落。

看到数据范围只有10组，每组10个，如果使用dfs暴力则复杂度为10*2^10，符合要求，则先尝试用dfs完成

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;

const int N = 15;
int t;
int n, flag;
int st[N];                         //记录飞机是否已经下降
int p[N][3];                       //记录三种状态，到达时间，最晚下降时间和降落所需时间

void dfs(int num, int ltime) {     //dfs函数，num为下降飞机数目，ltime为上次下降飞机结束时间
	if (flag)
		return;

	if (num >= n) {
		cout << "YES" << endl;
		flag = true;
	}

	for (int i = 1; i <= n; i ++) {

		if (!st[i]) {
			if (p[i][1] < ltime)
				return;
			st[i] = 1;

			if (ltime < p[i][0])
				dfs(num + 1, p[i][0] + p[i][2]);
			else
				dfs(num + 1, ltime + p[i][2]);
			st[i] = false;
		}
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin >> t;

	while (t --) {
		cin >> n;
		memset(st, 0, sizeof st);
		flag = false;

		for (int i = 1; i <= n; i ++) {

			cin >> p[i][0] >> p[i][1] >> p[i][2];
			p[i][1] += p[i][0];
		}

		dfs(0, 0);

		if (!flag)
			cout << "NO" << endl;

	}

	return 0;
}

运行成功，该题目的标签为状压dp，因此可以采用状压dp的做法，由于dp方面实在不擅长，会在之后通过刷acwing的dp的题目来提升一下dp题目的解题能力，在后续的博客中会持续更新。本题不再采用状压dp的方法进行完成。

第三题题目链接：4958. 接龙数列 - AcWing题库

对于一个长度为 K 的整数数列：A1,A2,...,AK，我们称之为接龙数列当且仅当 Ai 的首位数字恰好等于 Ai−1 的末位数字 (2≤i≤K)。

例如 12,23,35,56,61,11是接龙数列；12,23,34,56 不是接龙数列，因为 56 的首位数字不等于 34的末位数字。所有长度为1的整数数列都是接龙数列。

现在给定一个长度为 N的数列 A1,A2,...,AN，请你计算最少从中删除多少个数，可以使剩下的序列是接龙序列？

典型的线性dp的题目，从极值子序列的做法可以解出这道题目，那么dp数组中的dp[i][j]表示前i个数中， 以数字j结尾的最长接龙数列的长度。若第i个数的首位数字是a， 末位数字是b，dp[i]中相对于dp[i−1]变化的只有dp[i][b]， 表示第i个数只可能加到一个以a结尾的接龙数列中， 使得这个接龙数列长度加1并且结尾数字变成b。因此状态转移方程为dp[i][b]=max(dp[i - 1][b], dp[i][a] + 1)

（ps：这个状态转移确实很巧妙，可能是我见识的题目还不够多，在刚开始看到这个题目的时候丝毫没有头绪，知道是线性dp但是状态转移方程死活构造不出来）

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;

const int N = 10;
int n, ans;
int dp[N];

int main() {
	ios::sync_with_stdio(false);
	cin >> n;
	for(int i = 0; i < n; i ++)
	{
		string s;
		cin >> s;
		int a = s[0] - '0';
		int b = s.back() - '0';
		dp[b] = max(dp[b], dp[a] + 1);
		ans = max(ans, dp[b]);
	}
	cout << n - ans << endl;
	return 0;
}

参考了一篇博客的代码后写的，整体来说十分简练巧妙，用string存储数字很好的解决了数字难以处理第一位数的问题。（学会了string里面的back函数X

剩下除了较难的最后两题也会继续更新，未完待续......