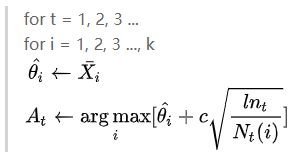如何用强化学习优化广告投放中的A/B Test

公众号后台回复“图书“，了解更多号主新书内容

     作者：会痛的stone

     来源：R语言工程化

A/B Test是决策科学的最常见方法之一。以广告投放为例，将客户群分为两组或多组，每组群体展示不同的广告形式。在测试结束时，针对测试结果选择最优的形式做大量投放。

然而A/B test有个很大的弊端，即一定程度上影响了部分用户的体验。尤其在测试内容存在极好、极差的情况下。

如果只有一个A/B test，那么成本可能是可控的，值得进行投资以发现最佳素材。但是，如果有多个A/B test，或者要测试多个版本，那么会有大量用户没有被提供最优体验，这可能会带来高昂的成本。

又或者，受成本限制无法进行一定量级的A/B Test，又或者成本能支持的A/B Test量级通过中心极限定理测算达不到目标精度要求的样本量。

理想情况下，我们希望能够迅速排除较差的版本，将测试集中到较优质的版本上。

多臂赌博机(Bandit算法)

在介绍他之前先简单聊聊强化学习。

强化学习就是学习做什么（即如何把当前的情境映射成动作）才能使得数值化的收益信号最大化。学习者必须自己通过尝试去发现哪些动作会产生最丰厚的收益，并且在某些情形下，策略动作不仅仅影响即时收益，也会影响后续收益。因此，试错与延迟收益是强化学习两个最重要最显著的特征。

为了获得大量的收益，强化学习智能体会更喜欢那些在过去为他有效产生过收益的动作（开发）；同时，为了发现这些动作，往往需要尝试从未选择的动作（试探）。因此，试探与开发的权衡成了强化学习独有的挑战。

并且，试探应是一直存在的，即便已经发现了当前收益最大的行为。因为在现实情况中，期望收益会随着时间变化而改变（非平稳），需要不断试探去发掘符合新情形下最大化收益的动作。

而多臂赌博机是强化学习的入门版本，背景是一个赌博机有k个杆，每拉一个杆都会产生一次收益，如何使收益最大化。其中，每个杆的收益可以是定值，也可以是服从某个分布（收益有波动）。至于如何通过尝试+开发来使收益最大化，这就引出了多臂赌博机的三种基本算法：ε-贪心、UCB（置信度上界）与Thompson Sampling（汤普森采样）。

• ε-greedy

每次动作选取精简版的逻辑如下：

每次行动有两个选择，一个是选择之前收益最大的动作（以1 - ε 的概率），一个是随机选取动作（以 ε 的概率）。这里ε为给定的概率值，取值在0~1之间。

如果要增加试探，则增大ε取值；相应的，如果想要增加开发，则减小ε取值。如果取ε等于0，则变成了贪心算法，贪心算法只适用于收益定值的情形下（局部最优即全局最优），在收益服从某种分布的情形下表现很差。

• UCB（置信度上界）

ε-贪心中以 ε 的概率选取随机动作，这种随机选取显然是盲目的，一个更好的策略是根据他们的潜力来选择可能更优的动作。但是完全变成贪心算法，从长远看效果很差。一个有效方法是按照以下公式选取动作：

c为给定的系数，Nt(i)为时刻t之前动作i被选择的次数。计算以上公式计算当前每个动作的收益情况，选取最大收益的动作，若某动作未被选取过，参照以上公式收益为无穷大，则该动作将会被选取。

所有动作最终都会被选取，但随着时间流逝，价值估计较低的动作以及已经被选取多次的动作再被选取的频率会变低。

• Thompson Sampling（汤普森采样）

TS是一种贝叶斯算法，从结构上看他与贪心算法类似，都是选取当前收益最大的动作。但与之不同的是，贪心算法是基于每个动作历史收益的矩估计（ 样本均值），TS是基于每个动作后验分布的采样值。

以两点问题为原型的两种算法示例：

其中，t为第t次行动，k为可供选择的动作数，为第i个动作期望收益的估计值（样本均值），意为第i个动作的期望收益的后验分布服从贝塔分布。

正是由于二项分布期望的共轭先验分布为贝塔分布的良好特性，使得每次更新后验分布变得非常容易，

其中，rt表示是否产生收益，是则为1，否则为0。也就是说，每次对应动作 后验贝塔分布的参数更新只是先前两个参数α或β加1即可。随着α + β 的值越大，分布曲线越集中，采样值也会越来越接近。

下面，以广告投放为背景测试下传统A/B Test与多臂赌博机算法的效果。

仿真模拟

有5个广告素材需要在同一投放平台进行A/B Test，假定5个素材的真实CTR分别是5%、6%、15%、25%、28%。我们会对5个素材各进行1000次曝光，并进行1000次模拟以求得每种算法的期望收益。本文仅考虑收益平稳且上下文无关的情况。

1. A/B Test

假定对实际CTR的预估误差必须有90%把握控制在5%以内，则根据中心极限定理最小样本量为：

根据计算结果，首先对5个素材各进行271次实验，之后对剩下的总次数平均分配到最优素材上。实现代码如下，

# A/B TEST
# setup 
horizon <- 1000L # 时长、试验次数
simulations <- 1000L # 模拟次数
conversionProbabilities <- c(0.05, 0.06, 0.15, 0.25, 0.28) # 真实CTR


nTestSample <- 271


clickProb <- rep(NA, simulations)
adDistMatrix <- matrix(NA, nrow = simulations, 
                       ncol = length(conversionProbabilities))
adDistMatrixAB <- matrix(NA, nrow = simulations, 
                         ncol = length(conversionProbabilities))
ABPayoff <- rep(NA, simulations)
# simulation
for(i in 1:simulations) {
  testSample <- sapply(conversionProbabilities,
                       function(x) sample(0:1, nTestSample, replace = TRUE, prob = c(1 - x, x))) # 模拟测试期所有广告点击情况
  
  testColumns <- (1:length(conversionProbabilities))[-which.max(colSums(testSample))] # 取出非最优广告
  
  p.values <- sapply(testColumns, function(x) prop.test(x = colSums(testSample[, c(x, which.max(colSums(testSample)))]),
                                                        n = rep(nTestSample, 2))$p.value) # 与最优广告做假设检验
  
  adsAfterABTest <- (1:length(conversionProbabilities))[- testColumns[which(p.values < 0.05)]] # A/B Test后选取最优广告进行投放
  
  # now just with the best performing ad(s)
  ABSample <- sapply(conversionProbabilities[adsAfterABTest],
                     function(x) sample(0:1, 
                                        round((horizon - nTestSample) * length(conversionProbabilities) / 
                                                length(adsAfterABTest), 0),
                                        replace = TRUE, prob = c(1 - x, x))) # 模拟Test后最优广告的投放情况
  
  clickProbTest <- sum(as.vector(testSample)) / length(unlist(testSample))
  clickProbAB <- sum(as.vector(ABSample)) / length(unlist(ABSample))
  
  clickProb[i] <- clickProbTest * (nTestSample / horizon) + clickProbAB * (1 - nTestSample / horizon)
  
  # 计算广告选取情况及收益情况
  adDistMatrix[i,] <- rep(1 / length(conversionProbabilities), length(conversionProbabilities))
  adDistributionAB <- rep(0, length(conversionProbabilities))
  adDistributionAB[adsAfterABTest] <- rep(1 / length(adsAfterABTest), length(adsAfterABTest))
  adDistMatrixAB[i,] <- adDistributionAB
  ABPayoff[i] <- (nTestSample * clickProbTest) + ((horizon - nTestSample) * clickProbAB)
}


# mean payoff
mean(ABPayoff)
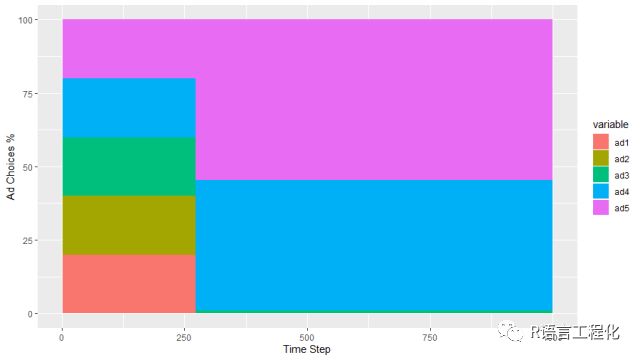
# about 236.0714

A/B Test总体在1000次曝光中平均带来了236次的点击，约占可能最好收益(280)的84％，这个结果还不错。再看下广告的选取情况，

在前271个试验中，广告被选取投放的比例是平均的。在接下来的500个试验中，最常看到广告5（效果最好的广告），其次是广告4，很少看到广告3。

如果把要求定的严格点，如90%把握误差控制在2%以内，则所需样本量提高，A/B Test效果更好。

2. ε-greedy

library(contextual)


# EPSILON GREEDY
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.06, 0.15, 0.25, 0.28)


bandit <- BasicBernoulliBandit$new(weights = conversionProbabilities)
policy <- EpsilonGreedyPolicy$new(epsilon = 0.10)
agent <- Agent$new(policy, bandit)


historyEG <- Simulator$new(agent, horizon, simulations)$run()


plot(historyEG, type = "arms",
     legend_labels = c('Ad 1', 'Ad 2', 'Ad 3', 'Ad 4', 'Ad 5'),
     legend_title = 'Epsilon Greedy',
     legend_position = "topright",
     smooth = TRUE)


summary(historyEG)

可以看到Epsilon Greedy（这里取ε = 0.1）算法可以迅速确定Ad 5是最优的，并且随着时间的推移而不断改进。总点击（收益）为250次，约占总可能最好收益的89.2％。这也比A/B Test试高出约6％，因为该算法能够比传统方法更快地开始利用最优质的广告。

3. UCB

library(contextual)


# UCB
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.06, 0.15, 0.25, 0.28)


bandit <- BasicBernoulliBandit$new(weights = conversionProbabilities)
policy <- UCB1Policy$new()
agent <- Agent$new(policy, bandit)


historyEG <- Simulator$new(agent, horizon, simulations)$run()


plot(historyEG, type = "arms",
     legend_labels = c('Ad 1', 'Ad 2', 'Ad 3', 'Ad 4', 'Ad 5'),
     legend_title = 'UCB',
     legend_position = "topright",
     smooth = TRUE)


summary(historyEG)

UCB总体收益为216，低于A/B Test。

4. Thompson Sampling

library(contextual)


# Thompson Sampling
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.06, 0.15, 0.25, 0.28)


bandit <- BasicBernoulliBandit$new(weights = conversionProbabilities)
policy <- ThompsonSamplingPolicy$new(alpha = 1, beta = 1)
agent <- Agent$new(policy, bandit)


historyThompson <- Simulator$new(agent, horizon, simulations)$run()


plot(historyThompson, type = "arms",
     legend_labels = c('Ad 1', 'Ad 2', 'Ad 3', 'Ad 4', 'Ad 5'),
     legend_title = 'Thompson Sampling',
     legend_position = "topright",
     smooth = TRUE)


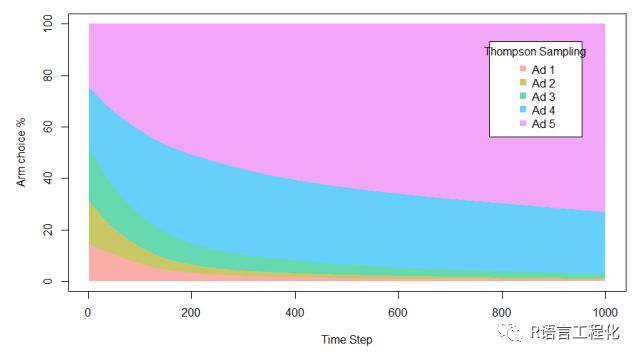
summary(historyThompson)

汤普森采样总体收益253，高于之前的所有算法，相对于A/B Test 收益提升7.2%，效果最好。

library(contextual)


# 比较三个bandit算法累计收益
horizon <- 1000L
simulations <- 1000L
conversionProbabilities <- c(0.05, 0.06, 0.15, 0.25, 0.28)


bandit             <- BasicBernoulliBandit$new(conversionProbabilities)


agents             <- list(Agent$new(EpsilonGreedyPolicy$new(0.1), bandit),
                           Agent$new(ThompsonSamplingPolicy$new(1.0, 1.0), bandit),
                           Agent$new(UCB1Policy$new(), bandit))


simulation         <- Simulator$new(agents, horizon, simulations)
history            <- simulation$run()


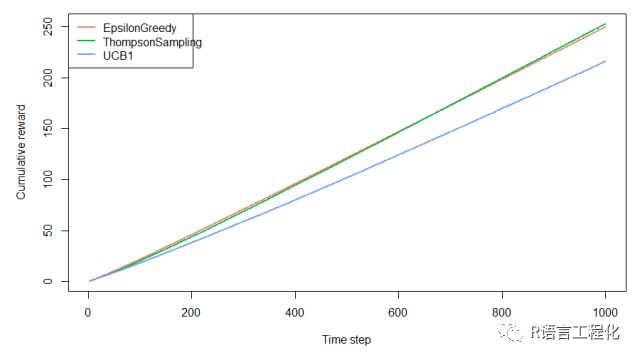
plot(history, type = "cumulative", regret = FALSE)

可以看到，UCB收益最低，ε-greedy起初较高，随后被TS超越。

总结

• A/B Test在精度或总体收益要求高，但成本不足以支撑最小样本量的情况下，总体效果不是特别理想。

• 强化学习整体效果好于A/B Test，能更快更好的利用最优质素材，尤其是汤普森采样。

• 强化学习本质上是进行策略优化的，本文仅是一个抛砖引玉、开拓思路的作用，具体应用可以扩展到很多业务场景，留待大家思考。

参考

1. https://www.inwt-statistics.com/read-blog/multi-armed-bandits-as-an-a-b-testing-solution.html

2. 强化学习（第2版）.[加] RichardS.Sutton，[美] AndrewG.Barto 著，俞凯 等 译

3. https://zhuanlan.zhihu.com/p/55254900

4. 概率论与数理统计教程（第2版）.茆诗松，程依明，濮晓龙 著

↑↑↑ 扫一扫就能关注我哦！

◆ ◆ ◆  ◆ ◆
麟哥新书已经在当当上架了，我写了本书：《拿下Offer-数据分析师求职面试指南》，目前当当正在举行活动，大家可以用相当于原价5折的预购价格购买，还是非常划算的：

数据森麟公众号的交流群已经建立，许多小伙伴已经加入其中，感谢大家的支持。大家可以在群里交流关于数据分析&数据挖掘的相关内容，还没有加入的小伙伴可以扫描下方管理员二维码，进群前一定要关注公众号奥，关注后让管理员帮忙拉进群，期待大家的加入。

管理员二维码：


猜你喜欢

● 卧槽！原来爬取B站弹幕这么简单
● 厉害了！麟哥新书登顶京东销量排行榜！
● 笑死人不偿命的知乎沙雕问题排行榜

● 用Python扒出B站那些“惊为天人”的阿婆主！
● 你相信逛B站也能学编程吗