C++ AVL 树
AVL树的概念
当数据有序或接近有序二叉搜索树将退化为单支树,此时二叉搜索树的搜索效率低下
解决方法:AVL树(降低树的高度,从而减少平均搜索长度)
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
· 它的左右子树都是AVL树
· 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
高度=右子树-左子树
AVL树的插入
与二叉搜索树稍有区别的是AVL树引入了平衡因子,AVL树节点设计成三叉链的形式
1 按照二叉搜索树的方式插入新节点
2 调整节点的平衡因子
设c表示新增节点 p表示父节点 bf表示平衡因子
首先要明确一点:新增可能会影响祖先(决定因素是子树高度是否发生变化):
1 如果子树高度不变,就不会继续向上影响祖先
2 如果子树高度变化,就会继续向上影响祖先
c新增后,p的平衡因子一定会需要调整:
新增节点在左子树:父节点的bf--
新增节点在右子树:父节点的bf++
在新增节点c插入前,父节点的bf(平衡因子)有如下三种情况:-1,0,1
在新增节点c插入后,父节点的bf更新情况有如下三种情况:0 正负1 正负2
1 若是父节点的bf更新后为0:说明未插入前父节点的bf是正负1(一边高一边低)
插入新增节点后父节点的bf被调整为0,此时满足AVL树的性质,直接插入成功
2 若是父节点的bf更新后为正负1:说明未插入前父节点的bf是0(左右子树高度一样)
此时以p父节点为根的子树高度增加,需要继续向上更新
3 若是父节点的bf更新后为正负2:则p父节点的平衡因子违反AVL树规则,需要对其进行旋转处理
AVL树的旋转
AVL树的旋转分为四种:右单旋 左单旋 先左单旋再右单旋 先右单旋再左单旋
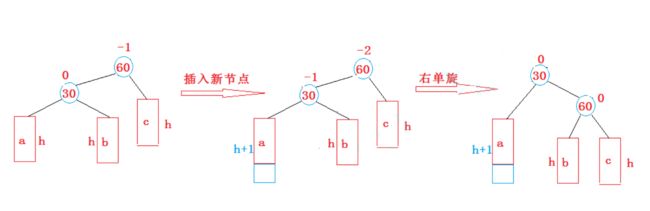
注意:1 30节点的右孩子可能存在,也可能不存在
2 60可能是根节点,也可能是子树
如果是根节点,旋转完成后,要更新根节点
如果是子树,可能是某个节点的左子树,也可能是右子树
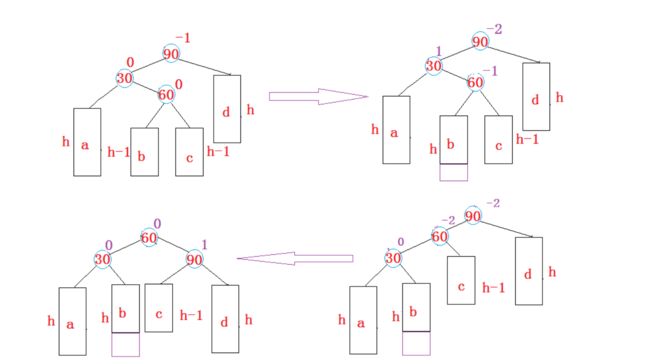
2 新节点插入较高右子树的右侧---右右:左单旋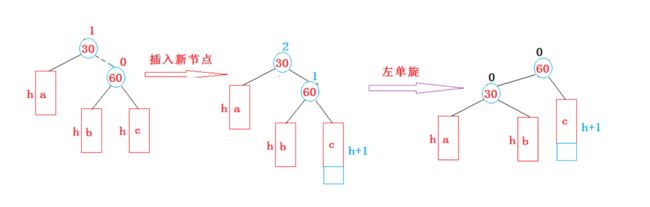
注意情况可以参考左单旋
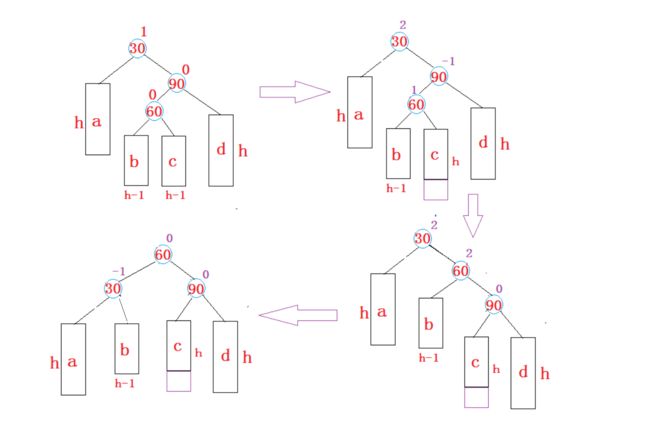
3 新节点插入较高左子树的右侧---左右:先左单旋再右单旋
将双旋变成单旋后再旋转:
先对30进行左单旋,然后再对90进行右单旋

总结:
若是以p节点为根的子树不平衡,即p节点的bf是正负2:
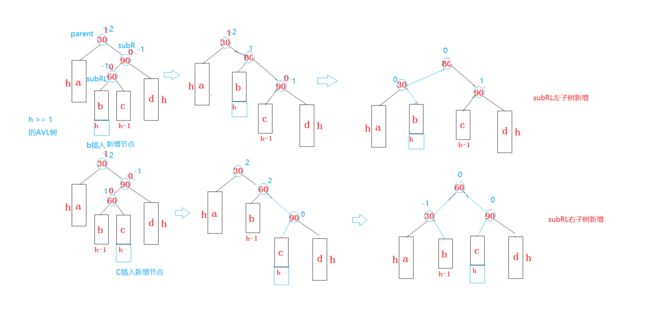
1 p节点的bf为2:说明p节点的右子树高,设p的右子树的根为subR
当subR的平衡因子为1时,执行左单旋
当subR的平衡因子为-1时,执行右左双旋
2 p节点的bf为-2: 说明p节点的左子树高,设p的左子树的根为subL
当subL的平衡因子为-1时,执行右单旋
当subL的平衡因子为1时,执行左右双旋
旋转完成后,原p为根的子树高度降低,已经平衡,无需再向上更新
AVL树的代码实现:
#pragma once
#include
template
struct AVLTreeNode
{
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;
pair _kv;
int _bf;//平衡因子 balance factor
AVLTreeNode(const pair&kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
template
class AVLTree
{
typedef AVLTreeNode Node;
public:
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//找到插入位置
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);//插入
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left= cur;
cur->_parent = parent;
}
while (parent)//更新平衡因子,可能会连续更新(即新增可能会影响祖先的bf):看子树高度是否变化
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)//新增前,父节点所在树一边高一边低,新增后刚好平衡两边
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)//新增前,父节点所在树已经平衡(左右子树两边一样高),新增节点打破平衡,使得子树高度增加
{
cur = parent;//继续向上调整
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)//父亲所在子树违反规则,需要调整处理(即旋转)
{
//旋转
if (parent->_bf == 2 && cur->_bf==1)//左单旋
{
RotateL(parent);
}
else if (parent->_bf == 2 && cur->_bf==-1)//右左双旋
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)//右单旋
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)//左右双旋
{
RotateLR(parent);
}
break;//1 旋转让这颗子树平衡了
//2 旋转降低了这颗子树的高度,恢复到跟插入前一样的高度,所以对上一层没有影响,不用继续更新
}
else
{
assert(false);
}
}
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
Node* parentParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (parent==_root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
parent->_bf = subR->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent==_root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
parent->_bf = subL->_bf = 0;
}
void RotateRL(Node*parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
//subRL自己就是新增
parent->_bf = subR->_bf = subRL->_bf = 0;
}
else if (bf == -1)
{
//subRL的左子树新增
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
else if (bf == 1)
{
//subRL的右子树新增
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
//subLR自己就是新增
parent->_bf = subL->_bf = subLR->_bf = 0;
}
else if (bf == -1)
{
//subRL的左子树新增
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if (bf == 1)
{
//subRL的右子树新增
parent->_bf = 0;
subL->_bf = -1;
subLR->_bf = 0;
}
else
{
assert(false);
}
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()//AVL树的验证:1 为二叉搜索树,即中序遍历得到有序序列 2 为平衡树:每个节点子树高度差的绝对值不超过1 && 节点的平衡因子是否计算正确
{
return _IsBalance(_root);
}
int Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
private:
void _InOrder(Node * root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
bool _IsBalance(Node * root)
{
if (root == nullptr)
return true;
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
if (rightHeight - leftHeight != root->_bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
private:
Node* _root = nullptr;
}; 验证:
#include
#include
using namespace std;
#include"AVLTree.h"
int main()
{
const int N = 30;
vector v;
v.reserve(N);
srand(time(0));
for (size_t i = 0; i < N; i++)//产生N个随机数
{
v.push_back(rand());
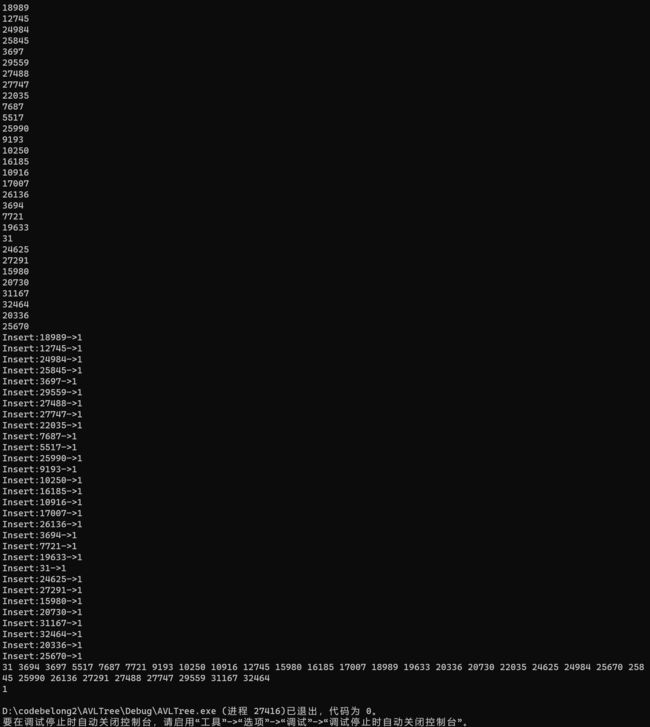
cout << v.back() << endl;
}
AVLTree t;
for (auto e : v)
{
t.Insert(make_pair(e, e));
cout << "Insert:" << e << "->" << t.IsBalance() << endl;
}
t.InOrder();
cout << t.IsBalance() << endl;
return 0;
}