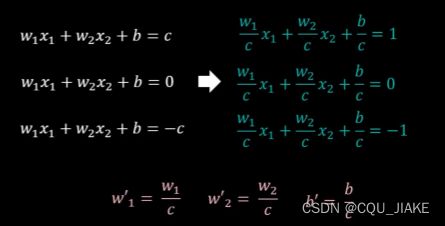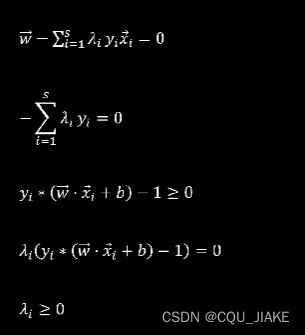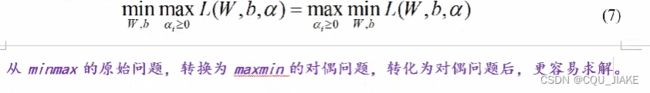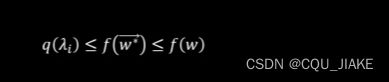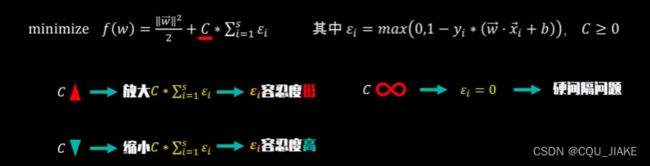1.22SVM(对偶性,KKT条件,核函数(高斯核函数RBF,参数伽马),软间隔问题(对误差容忍,参数C),总结,例题),SVM流程,代码,划分指定类数
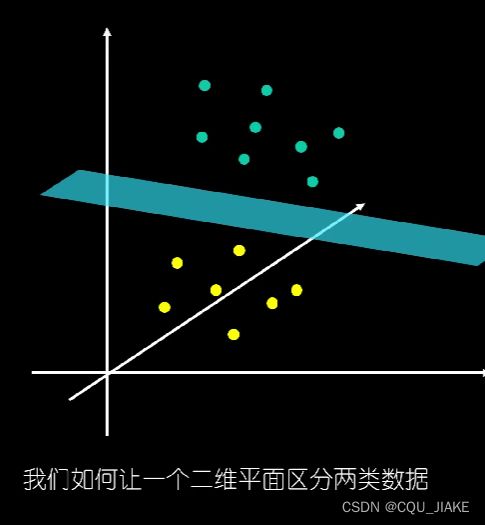
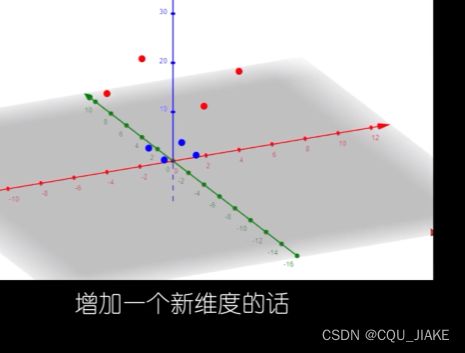
就是说数据有多维的特性,然后依据特性在坐标系种存在点,就是画一个面来分割不同的点,从而实现数据的分类
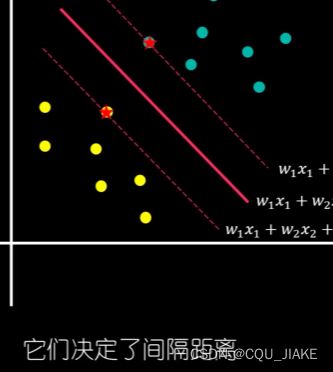
W为X对应的权重
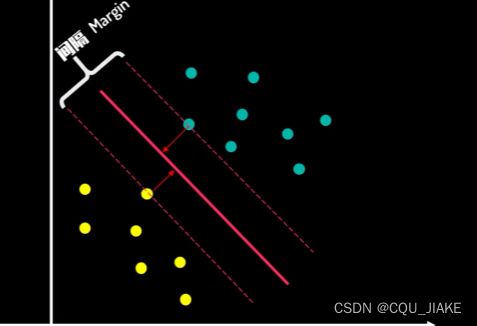
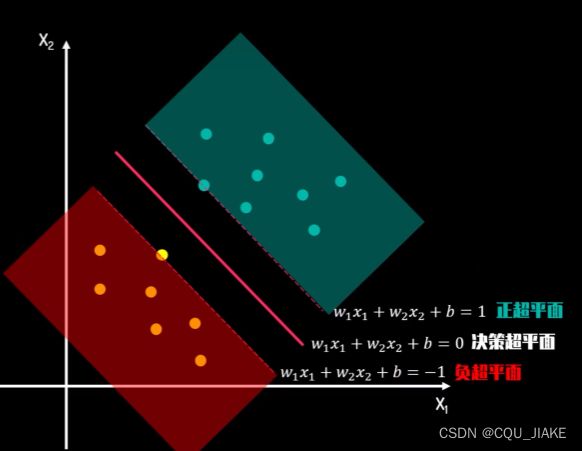
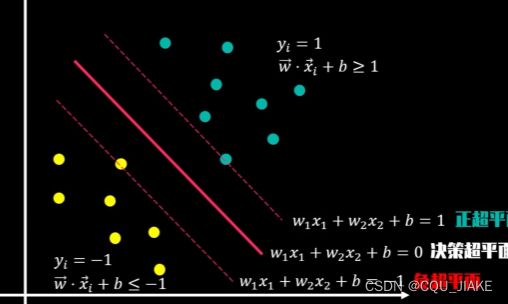
可以转化为求解两类数据的最大间隔问题
就是说,这个超平面是依据数据集计算得到的,然后这个数据是哪个类的,特征为哪些都是事先确定的,计算的目的是找一个超平面,使支持向量的间距最大
对于那些在决策超平面周围,或者说是支持向量很近的点
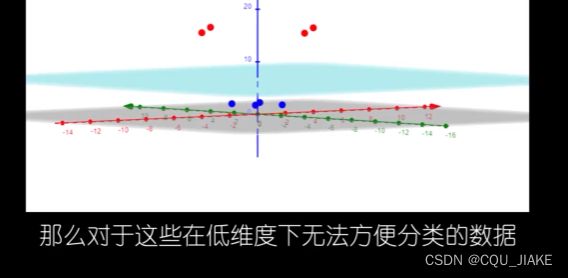
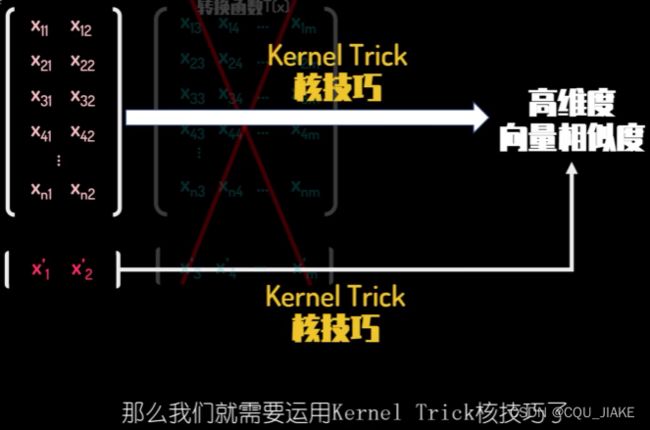
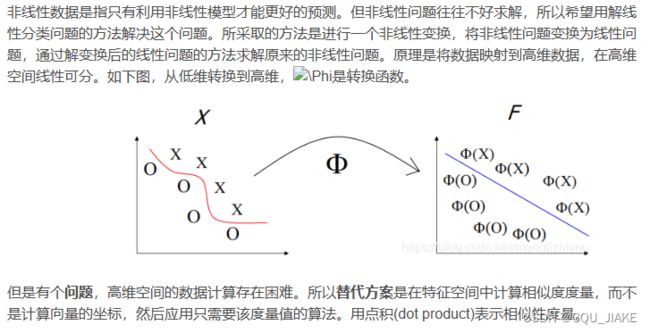
合适的维度转换函数,将低维转化为高维,然后在高纬度下求解SVM
左侧矩阵是说的有n个数据,每个数据有两个维度的信息,即数据集,然后升维,变为nm矩阵,运算就确定超平面
xm-xn再乘cos,可以理解为数据升维后又投影到这个超平面上,就是超平面上两个支持向量之间的距离
这个点乘,特征向量是和超平面垂直的;就是说最后找出来的超平面的方程,决定特征向量是和它垂直的,就是说特征向量是n维,那么超平面就是n-1维,且满足特征向量垂直超平面 、
数据是分布在n维空间中的,数据向量做差就可以认为是降了一维,和特征向量点乘就是在超平面上投影到特征向量的距离,目的是要使这个距离最大
如果约束条件为等式,就可以直接拉格朗日数乘 ;为不等式,就转为等式,再用拉格朗日数乘
这个w是权重,然后数据点都是依据所给定的权重特征分布在空间当中,然后要依据特征去分类不同的点,自然就是要去权衡各个特征在分类中所占的比例,怎么分配这些比例,从而使得可以更好的区分不同的单词
第一种情况是说数据点不在正负超平面上
对偶问题
KKT条件
KKT条件(Karush-Kuhn-Tucker条件)是一组用于非线性规划问题的约束条件,由Karush、Kuhn和Tucker在20世纪50年代提出。KKT条件是一种重要的优化理论,广泛应用于数学规划和最优化问题中。
KKT条件是非线性规划中的一组必要条件,用于判断一个点是否为最优解。它由四个部分组成:
1. 原始可行性条件(Primal Feasibility Condition):指决策变量对应的值必须满足约束条件。
这个就是说满足约束条件
2. 对偶可行性条件(Dual Feasibility Condition):指拉格朗日乘子应大于等于零,以满足约束条件的非负性。
3. 可行性间隙条件(Complementary Slackness Condition):指原始变量和拉格朗日乘子的乘积为零,即对于每个约束,要么其对应的拉格朗日乘子为零,要么其对应的约束等式成立。
4. 梯度条件(Gradient Condition):指目标函数对应的梯度向量与拉格朗日乘子加权之和为零。
只有当一个解满足这四个条件时,才能被认为是最优解。这些条件提供了在非线性规划问题中判断解优劣的准则,并提供了构造优化算法的理论基础。
KKT条件在很多优化算法中被使用,比如求解支持向量机(SVM)的SMO算法就是基于KKT条件进行优化。
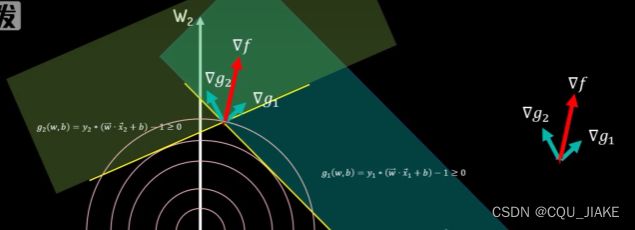
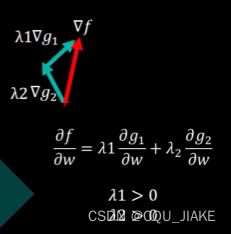
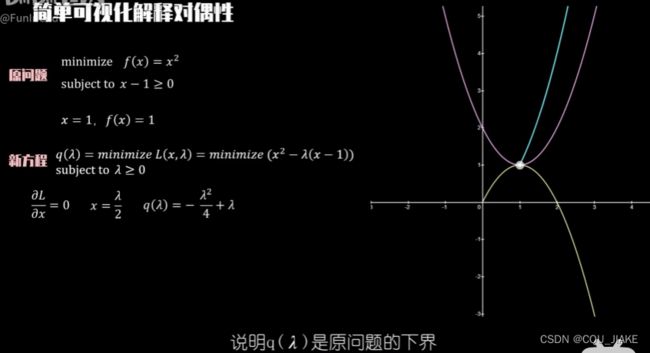
就是说通过拉格朗日,可以把原约束转化为与参数朗姆达有关的方程,然后问题就转化为求这个函数的极值,这个极值对应的就是朗姆达星所对应的地方的值 ![]()




是说通过KKT条件,使朗姆达非负,然后在这个条件下最优化
最优解只与支持向量的点积结果决定,也就是只与支持向量的空间相似度所决定
为了计算支持向量的
核函数,高斯核函数RBF
1、核函数定义
将原始空间中的向量作为输入向量,并返回特征空间(转换后的数据空间,可能是高维)中向量的点积的函数称为核函数。
使用内核,不需要显式地将数据嵌入到空间中,因为许多算法只需要图像向量之间的内积(内积是标量);在特征空间不需要数据的坐标。
这个核函数计算出来的结果,直接就是这两个向量之间的空间相似度;自变量是两个向量间的距离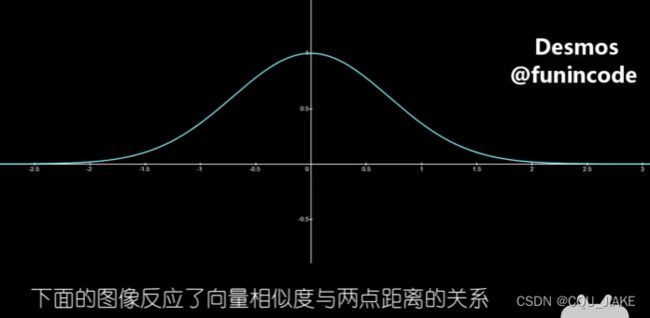


选择合适的伽马值很重要




对于扁平的RBF,伽马值小,那么越容易认为它们之间有相似度;当伽马值变大
就是说伽马越小,越容易融合成为一类;越大,就越不容易融合
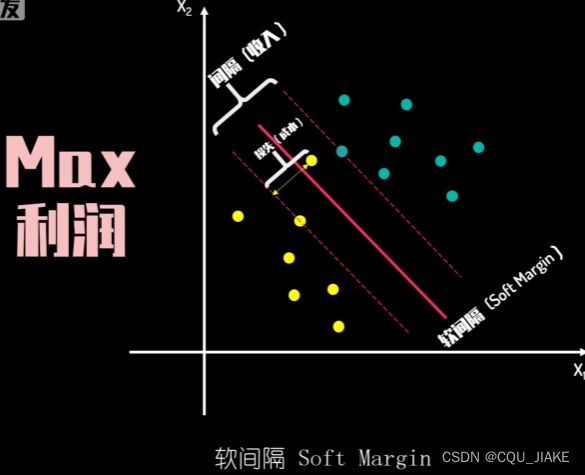
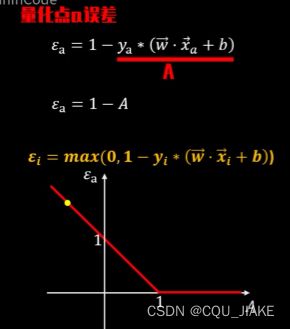
软间隔
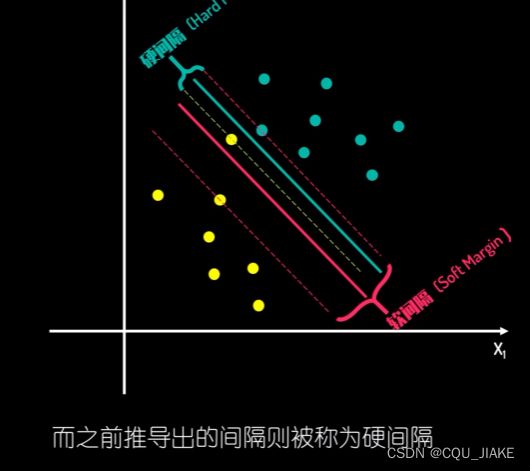
在硬件隔问题中,是要让两个最近的支持向量到超平面的间距最大,在高维时使用核函数,可以转为间距与特征向量组成倒数关系,就是说特征向量绝对值越大,间隔越小,划分效果越不好
因为目的是要最大化支持向量间的距离
所以间隔应该越大越好,但如果间隔越大,就越容易出现处于正负超平面间的点,就会产生损失

选择合适的参数C很重要
再理解+总结SVM
在面对非线性SVM划分,可以使用高斯核函数
对于高斯核函数,伽马值越小,对距离的容忍度越大;就是说小伽马值更容易使两个相差不近的点被划分为同一类当中,导致预测精度的下降
而对大伽马值,就依据训练集上的点,只在其训练集周围点的附近,距离很近的地方形成分类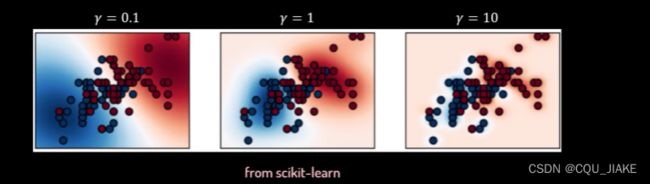
就是把伽马认为成是反映的辐射范围,是训练集上的点向周围数据的辐射范围,伽马值越小,那么每个点向周围辐射的范围就越大,对距离的容忍度就越大,在它周围的点越容易被视为同类;反之,伽马值越大,辐射范围就越小,只有离得很近才会被认为成同类,不然不会被辐射为同类
核函数是把原来非线性的升维到高维里,使其变为线性的,在线性里完成划分
整体流程
就是下载数据,然后数据预处理,划分数据集,可视化,调用模型,然后交叉验证和混淆矩阵,
% 加载数据集
load fisheriris
X = meas(:, 1:2);
Y = (strcmp(species, 'versicolor')) * 2 - 1; % 将类别转换为二元标签 (+1, -1)
N = size(X, 1); % 样本数量
% 训练SVM
svm = fitcsvm(X, Y);
% 使用训练好的SVM进行预测
Y_pred = predict(svm, X);
% 可视化结果
gscatter(X(:,1), X(:,2), Y);
hold on;
svmplot(svm);
hold off;
要对SVM进行调优,可以尝试调整以下参数:
1. 核函数(Kernel Function):尝试不同的核函数,如线性核函数、多项式核函数或高斯核函数,选择最适合数据集的核函数。
2. 超参数C:调整参数C来改变容错限度,即误分类的惩罚因子。较大的C值会导致更严格的分类,但可能出现过拟合问题。
3. 超参数γ:仅适用于高斯核函数,调整参数γ来控制决策边界的曲率。较小的γ值产生平滑的决策边界,较大的γ值产生更复杂的决策边界,但可能过度拟合。
以下是一个示例代码,展示如何使用交叉验证来调优SVM的C和γ参数:
% 加载数据集
load fisheriris
X = meas(:, 1:2);
Y = (strcmp(species, 'versicolor')) * 2 - 1; % 将类别转换为二元标签 (+1, -1)
% 创建参数搜索范围
C_values = [0.01, 0.1, 1, 10, 100];
gamma_values = [0.01, 0.1, 1, 10, 100];
% 使用交叉验证进行参数调优
svm_model = fitcsvm(X, Y, 'OptimizeHyperparameters', {'BoxConstraint', 'KernelScale'}, 'HyperparameterOptimizationOptions', struct('AcquisitionFunctionName','expected-improvement-plus', 'MaxObjectiveEvaluations', 20, 'ShowPlots', false, 'Verbose', 0), 'CVPartition', cvpartition(Y, 'KFold', 5), 'KernelFunction', 'rbf', 'BoxConstraint', C_values, 'KernelScale', gamma_values);
% 最佳超参数
best_C = svm_model.BestHyperparameters.BoxConstraint;
best_gamma = svm_model.BestHyperparameters.KernelScale;
% 训练最佳SVM模型
best_svm = fitcsvm(X, Y, 'KernelFunction', 'rbf', 'BoxConstraint', best_C, 'KernelScale', best_gamma);
% 使用最佳模型进行预测
Y_pred = predict(best_svm, X);
% 可视化结果
gscatter(X(:,1), X(:,2), Y);
hold on;
svmplot(best_svm);
hold off;
在上述代码中,我们首先选择了一些要调优的超参数的候选值(C_values和gamma_values)。然后,我们使用 `fitcsvm` 函数和交叉验证进行参数调优。在这个过程中,我们指定了参数搜索范围、优化目标函数和其他相关设置。
通过 `svm_model.BestHyperparameters` 可以获得调优后的最佳超参数值。然后,使用最佳超参数重新训练一个新的SVM模型 `best_svm`。
最后,使用最佳模型 `best_svm` 对训练数据进行预测,并使用 `gscatter` 和 `svmplot` 函数将数据和决策边界可视化出来。
例题
K折验证
就是把数据集再重新划分,进而继续校验模型
SVM实现多划分
支持向量机(SVM)可以进行多类分类。有两种主要的方法可以实现多类分类:
-
一对多(One-vs-Rest)方法:对于N个类别,训练N个二元分类器,每个分类器将一个类别作为正例,将其他所有类别作为负例。在预测时,将输入样本输入N个分类器中的每一个,并选择具有最高置信度或概率的类别作为预测结果。
-
一对一(One-vs-One)方法:对于N个类别,训练N*(N-1)/2个二元分类器,每个分类器只区分两个类别。在预测时,将输入样本输入N*(N-1)/2个分类器中的每一个,并使用投票或其他方法来决定最终的分类结果。
在MATLAB中,可以使用 fitcecoc 函数来进行多类分类,该函数使用一对一的方法实现多类分类。以下是一个示例代码,展示如何使用SVM进行多类分类:
% 加载数据集
load fisheriris
X = meas(:, 1:2);
Y = species;
% 训练多类SVM模型
svm_model = fitcecoc(X, Y);
% 使用训练好的多类SVM模型进行预测
Y_pred = predict(svm_model, X);
% 计算准确率
accuracy = sum(Y_pred == Y) / numel(Y) * 100;
% 可视化结果
gscatter(X(:,1), X(:,2), Y);
hold on;
h = svmplot(svm_model);
hold off;
legend(h, svm_model.ClassNames);
在上述代码中,我们加载了鸢尾花数据集 fisheriris,选择了前两个特征作为输入 X,类别作为标签 Y。
然后,使用 fitcecoc 函数训练一个多类SVM模型 svm_model,该模型使用一对一方法进行多类分类。
接下来,使用训练好的模型 svm_model 对训练数据 X 进行预测,得到预测结果 Y_pred。
最后,计算分类准确率,并使用 gscatter 和 svmplot 函数将数据和决策边界可视化出来。
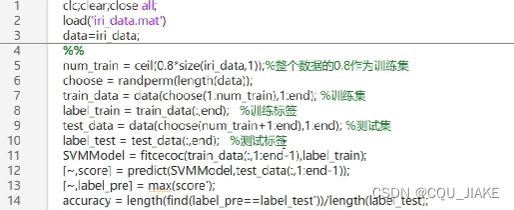
指定类数
% 加载数据集
load fisheriris
X = meas(:, 1:2);
Y = species;
% 提取要分类的类别
class1 = 'setosa';
class2 = 'versicolor';
classes = {class1, class2};
% 将类别转换为二元标签
Y_binary = double(ismember(Y, classes));
Y_binary(Y_binary == 0) = -1;
% 训练一对一SVM模型
svm_model = fitcsvm(X, Y_binary, 'KernelFunction', 'linear', 'ClassNames', classes);
% 使用训练好的一对一SVM模型进行预测
Y_pred = predict(svm_model, X);
% 可视化结果
gscatter(X(:,1), X(:,2), Y);
hold on;
h = svmplot(svm_model);
hold off;
legend(h, svm_model.ClassNames);