C++面试:散列表
目录
1. 散列表的基本概念
散列表的定义
散列函数
哈希冲突
2. 处理冲突的方法
链地址法(Separate Chaining)
开放地址法
再散列
3. 散列表的性能分析
1. 平均查找长度(ASL)
2. 负载因子(Load Factor)
代码示例:计算负载因子和模拟查找
4. C++ 中的散列表实现
1. std::unordered_map
2. std::unordered_set
5. 散列表的应用场景
1. 快速数据访问
2. 数据去重
3. 实现映射和集合
6. 面试常见问题
1. 如何选择合适的散列函数?
2. 散列冲突的处理方式及其优缺点?
3. 如何根据场景选择合适的散列表实现(例如 std::unordered_map vs std::map)?
散列表(Hash Table),也常称为哈希表,在 C++ 中是一种重要的数据结构,常用于快速的数据存储和查找。面试时,对散列表的理解和应用是衡量候选人技术能力的一个重要方面。
1. 散列表的基本概念
-
散列表的定义
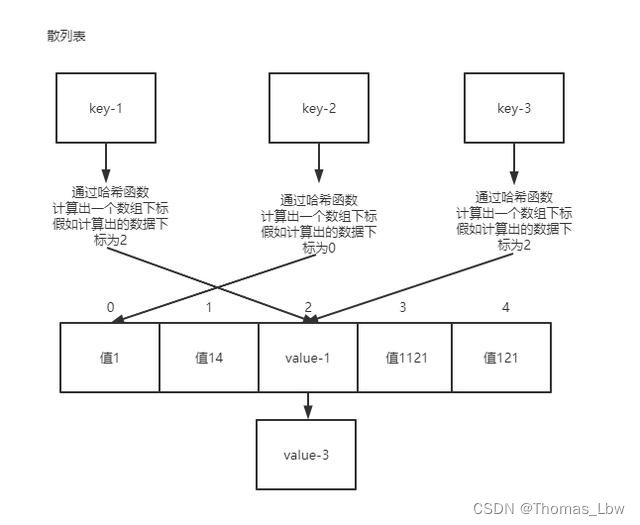
散列表(哈希表)是一种使用散列函数组织数据,以支持快速插入和搜索的数据结构。它的核心思想是利用一个函数(称为散列函数或哈希函数),将输入(通常是一个键)映射到一个位置(即索引),然后在该位置存储值。这种方法提供了快速的数据查找速度,因为直接通过键计算出的索引访问数据,而不需要像在列表或树结构中那样逐个搜索。
-
散列函数
散列函数是散列表中的核心组成部分,其作用是将输入的键转换成散列表中的索引。一个好的散列函数应该满足以下条件:
- 一致性:相同的输入总是产生相同的输出(索引)。
- 高效计算:散列函数应该容易计算,不应该有复杂的运算。
- 均匀分布:散列函数应该将键均匀分布在散列表中,以减少冲突的可能性。
-
哈希冲突
哈希冲突发生在两个或多个键被映射到散列表的同一位置时。这种情况是不可避免的,因为散列表的大小是有限的,而可能的键的数目通常是无限的。处理哈希冲突的方法很重要,因为它们会影响散列表的性能。
2. 处理冲突的方法
链地址法(Separate Chaining)
链地址法是处理散列冲突的一种常用方法。它的基本思想是:
- 链表存储:每个散列表槽位(bucket)都关联一个链表。当多个键散列到同一个槽位时,它们的值将存储在同一个链表中。
- 插入操作:当插入一个新的键值对时,首先通过散列函数确定其槽位,然后将键值对添加到对应槽位的链表中。
- 查找操作:要查找一个键,先计算它的散列值定位到相应槽位,然后在链表中遍历查找。
- 删除操作:类似于查找,先定位到槽位,然后在链表中遍历以找到并删除元素。
在链地址法中,每个散列表的槽位关联一个链表。当不同的键映射到同一个槽位时,它们的值会被存储在同一个链表中。
#include
#include
#include
template
class HashTable {
private:
static const int HASH_GROUPS = 10;
std::list> table[HASH_GROUPS];
public:
bool isEmpty() const;
int hashFunction(K key);
void insertItem(K key, V value);
void removeItem(K key);
V searchByKey(K key);
void printTable();
};
// 示例方法实现(如 hashFunction, insertItem, etc.)
开放地址法
开放地址法是另一种常用的冲突解决方法,它在散列表本身寻找空槽位:
- 线性探测:当发生冲突时,顺序检查表中的下一个槽位,直到找到空槽位。
- 二次探测:与线性探测类似,但搜索的间隔是二次方数列(1, 4, 9, 16, ...)。
- 双重散列:使用一系列的散列函数。如果第一个散列函数导致冲突,就尝试第二个散列函数,依此类推。
开放地址法的优点是不需要额外的存储空间来处理冲突,但是当散列表接近满时,性能会下降。
在开放地址法中,所有的元素都直接存储在散列表数组中。当发生冲突时,算法会寻找另一个空槽位。
#include
#include
template
class HashTable {
private:
static const int HASH_TABLE_SIZE = 10;
std::pair table[HASH_TABLE_SIZE];
K EMPTY_KEY;
public:
HashTable(K emptyKey);
int hashFunction(K key);
void insertItem(K key, V value);
void removeItem(K key);
V searchByKey(K key);
};
// 示例方法实现(如 hashFunction, insertItem, etc.)
再散列
再散列是通过使用第二个(或多个)散列函数来解决冲突的方法。它的基本思想是:
- 当插入操作导致冲突时,使用第二个散列函数计算新的槽位。
- 如果第二个散列函数还是导致冲突,可以尝试第三个散列函数,依此类推。
- 这种方法通常与其他方法(如链地址法或开放地址法)结合使用。
再散列的优点在于它可以在不同的散列函数之间分散冲突,减少了单个散列函数可能导致的冲突集中。然而,选择合适的散列函数组合对于性能至关重要。
#include
#include
template
class HashTable {
private:
static const int HASH_TABLE_SIZE = 10;
std::pair table[HASH_TABLE_SIZE];
K EMPTY_KEY;
int hashFunction1(K key);
int hashFunction2(K key);
public:
HashTable(K emptyKey);
void insertItem(K key, V value);
void removeItem(K key);
V searchByKey(K key);
}; 3. 散列表的性能分析
散列表的性能分析主要集中在两个方面:平均查找长度(Average Search Length, ASL)和负载因子(Load Factor)。理解这两个概念对于设计高效的散列表至关重要。
1. 平均查找长度(ASL)
平均查找长度是衡量散列表效率的重要指标,它分为两部分:
- 成功平均查找长度(ASL成功):在表中找到元素所需的平均比较次数。
- 不成功平均查找长度(ASL不成功):在表中未找到元素所需的平均比较次数。
ASL取决于多种因素,包括散列函数的质量、处理冲突的方法和散列表的负载因子。
2. 负载因子(Load Factor)
负载因子是散列表已填充的程度的量度,定义为表中已有元素数量与散列表总空间的比例。其公式为:
- 负载因子越高,意味着散列表中的冲突可能性越大,这会增加查找时间。
- 一般而言,当负载因子增长到一定阈值(如0.7或0.75)时,会执行散列表的扩容操作(rehashing),以保持操作的效率。
代码示例:计算负载因子和模拟查找
下面是一个简单的 C++ 示例,展示了如何在散列表实现中计算负载因子,并模拟查找过程以估计平均查找长度。
#include
#include
#include
template
class HashTable {
private:
static const int HASH_TABLE_SIZE = 10;
std::list> table[HASH_TABLE_SIZE];
int numElements = 0; // 跟踪插入的元素数量
int hashFunction(K key) {
return key % HASH_TABLE_SIZE;
}
public:
void insertItem(K key, V value) {
int index = hashFunction(key);
table[index].push_back(std::make_pair(key, value));
numElements++;
}
double loadFactor() const {
return (double)numElements / HASH_TABLE_SIZE;
}
int searchByKey(K key) {
int index = hashFunction(key);
int searchCount = 0;
for (auto it = table[index].begin(); it != table[index].end(); it++) {
searchCount++;
if (it->first == key) {
return searchCount; // 返回查找次数
}
}
return searchCount; // 如果未找到,返回查找次数
}
};
int main() {
HashTable hashTable;
// 插入元素
hashTable.insertItem(1, "value1");
hashTable.insertItem(2, "value2");
hashTable.insertItem(3, "value3");
// 计算负载因子
std::cout << "Load Factor: " << hashTable.loadFactor() << std::endl;
// 模拟查找
int searchCount = hashTable.searchByKey(2);
std::cout << "Search Count: " << searchCount << std::endl;
return 0;
}
这个示例中,HashTable 类实现了基本的插入和查找操作,并计算了负载因子。searchByKey 方法返回查找一个元素所需的步骤数,从而可以用来估计 ASL。在实际应用中,ASL 的计算会更加复杂,通常涉及对大量操作的统计分析。
在面试中,展示你如何通过代码实现和分析这些性能指标,可以证明你对散列表及其性能优化有深入的理解。这对于腾讯等公司的 C++ 后台开发职位是非常重要的。
4. C++ 中的散列表实现
在 C++ 中,标准库提供了两种基于散列表的容器:std::unordered_map 和 std::unordered_set。这些容器提供了高效的插入、查找和删除操作。
1. std::unordered_map
std::unordered_map 是一种关联容器,存储键值对,其中键是唯一的。它提供快速的查找、插入和删除操作,平均时间复杂度为 O(1)。
特点:
- 基于散列表实现。
- 键值对的存储不按特定顺序排列。
- 提供单个元素的插入、访问和删除操作。
- 允许自定义散列函数和相等判断凭据。
#include
#include
int main() {
std::unordered_map map;
// 插入元素
map[1] = "apple";
map[2] = "banana";
map[3] = "cherry";
// 访问元素
std::cout << "map[2] = " << map[2] << std::endl;
// 查找元素
if (map.find(3) != map.end()) {
std::cout << "Found cherry!" << std::endl;
}
// 删除元素
map.erase(2);
return 0;
}
2. std::unordered_set
std::unordered_set 是一个集合容器,它存储唯一的元素,不允许重复。它的内部实现也是基于散列表。
特点:
- 每个元素的值即是其键。
- 不允许重复的元素。
- 提供快速的查找、插入和删除操作,平均时间复杂度为 O(1)。
- 元素的存储顺序是不确定的。
#include
#include
int main() {
std::unordered_set set;
// 插入元素
set.insert(1);
set.insert(2);
set.insert(3);
// 查找元素
if (set.find(2) != set.end()) {
std::cout << "Found 2" << std::endl;
}
// 删除元素
set.erase(2);
// 遍历集合
for (int number : set) {
std::cout << number << std::endl;
}
return 0;
}
在这两个例子中,std::unordered_map 和 std::unordered_set 提供了高效的散列功能,非常适合需要快速查找和存储唯一元素的场景。在面试中,你可能会被要求展示对这些容器的理解和应用,特别是在谈到性能优化和数据结构选择时。了解它们的内部工作原理和适用场景可以帮助你在腾讯等公司的 C++ 后台开发面试中脱颖而出。
5. 散列表的应用场景
1. 快速数据访问
散列表因其平均时间复杂度为 O(1) 的查找性能而被广泛用于需要快速数据访问的场景。
- 缓存系统:散列表是构建缓存系统(如 Memcached、Redis)的理想数据结构。在这些系统中,可以通过键快速检索存储的数据项,从而提高数据访问速度,并减少对主存储(如硬盘)的访问。
- 数据库索引:数据库中的索引通常使用散列表来实现,以加快数据的检索速度。通过将键(如数据库行的主键)映射到数据的位置,散列表使得数据库能够快速找到存储的记录。
这个示例演示了如何使用 std::unordered_map 实现一个基础的内存缓存系统。
#include
#include
#include
class MemoryCache {
private:
std::unordered_map cache;
public:
void set(const std::string& key, const std::string& value) {
cache[key] = value;
}
std::string get(const std::string& key) {
auto it = cache.find(key);
if (it != cache.end()) {
return it->second;
}
return "Not found";
}
};
int main() {
MemoryCache myCache;
// 设置缓存值
myCache.set("key1", "value1");
myCache.set("key2", "value2");
// 获取缓存值
std::cout << "key1: " << myCache.get("key1") << std::endl;
std::cout << "key3: " << myCache.get("key3") << std::endl; // 未设置的键
return 0;
}
2. 数据去重
在需要快速检查和删除重复元素的场合,散列表提供了一个高效的解决方案。
- 去重操作:散列表可以用来快速检测和处理重复的数据。例如,在处理大量数据时,可以使用散列表来检查某个元素是否已经存在。如果散列表中已存在该元素,则可以确定该元素是重复的,从而进行相应的去重处理。
#include
#include
#include
int main() {
std::vector numbers = {1, 2, 2, 3, 4, 4, 4, 5};
std::unordered_set uniqueNumbers;
for (int number : numbers) {
uniqueNumbers.insert(number);
}
std::cout << "Unique numbers: ";
for (int number : uniqueNumbers) {
std::cout << number << " ";
}
std::cout << std::endl;
return 0;
}
3. 实现映射和集合
散列表也用于实现映射和集合这类抽象数据类型。
- 映射(字典):在很多编程语言中,映射或字典结构是用散列表实现的。映射存储键值对,每个键映射到一个值。例如,C++ 的
std::unordered_map就是使用散列表实现的。 - 集合:集合是一种只存储唯一元素的数据结构。散列表的唯一性特性使其成为实现集合的理想选择。C++ 的
std::unordered_set是一个基于散列表实现的集合。
#include
#include
#include
#include
int main() {
// 使用 unordered_map 实现字典
std::unordered_map wordCount;
wordCount["apple"] = 1;
wordCount["banana"] = 2;
for (const auto& pair : wordCount) {
std::cout << pair.first << ": " << pair.second << std::endl;
}
// 使用 unordered_set 实现集合
std::unordered_set fruitSet;
fruitSet.insert("apple");
fruitSet.insert("banana");
fruitSet.insert("cherry");
std::cout << "Fruits in set: ";
for (const std::string& fruit : fruitSet) {
std::cout << fruit << " ";
}
std::cout << std::endl;
return 0;
}
6. 面试常见问题
1. 如何选择合适的散列函数?
选择合适的散列函数是关键,因为它直接影响到散列表的性能。合适的散列函数应该满足以下条件:
- 均匀性:散列函数应该将键均匀地分布在散列表中,以减少冲突的概率。
- 计算效率:散列函数的计算应该快速,避免复杂的运算,因为它会在每次插入和查找操作中被调用。
- 适应数据特性:散列函数应根据数据的特性来选择。例如,对于字符串数据,可以使用多项式滚动哈希;对于整数,可能使用模运算或位运算等。
2. 散列冲突的处理方式及其优缺点?
散列冲突的处理方式主要有两种:链地址法和开放地址法。
- 链地址法(Separate Chaining):
- 优点:简单,容易实现;链表可以无限增长,不受散列表大小限制。
- 缺点:需要额外的内存空间存储指针;缓存性能不如开放地址法好。
- 开放地址法(Open Addressing,如线性探测、二次探测):
- 优点:所有数据都存储在数组中,可以更好地利用缓存;数据存储紧凑,节省空间。
- 缺点:当散列表接近满时,插入和查找的性能会下降;删除操作较复杂。
3. 如何根据场景选择合适的散列表实现(例如 std::unordered_map vs std::map)?
选择合适的散列表实现取决于具体的应用场景:
- std::unordered_map:
- 适用场景:当需要快速的查找、插入和删除操作,且不关心元素的顺序时。
- 特点:基于哈希表实现,提供平均常数时间的性能;元素无序。
- std::map:
- 适用场景:当需要有序的元素集合,或者经常进行范围查询时。
- 特点:通常基于红黑树实现,元素按键排序;查找、插入和删除操作的时间复杂度为 O(log n)。