轻松搞定前缀和

一维前缀和：

概念

对于一个长度为n的列表a

前缀和为:

例如: ，前缀和数组 

和高中学的数列的an和sn的关系是一样的，本质是容斥定理，感兴趣的自行搜索。

一维具体实现代码（模板）：

def get_presum(a):#下标从0开始
    n = len(a)
    sum = [0] * n
    sum[0] = a[0]
    for i in range(1,n):
        sum[i] = sum[i - 1] + a[i]
    return sum
def get_sum(sum, l, r):
    if l == 0:
        return sum[r]
    else:
        return sum[r] - sum[l - 1]
a = [1,2,3,4,5]
sum = get_presum(a)
print("a = ",a)
print("sum = ", sum)
print(get_sum(sum,2,3))

运行结果：

还有一种更简便的方法，就是利用强大的库（使用迭代器算前缀和），但是下标默认从0开始。

from itertools import accumulate #求出a的前缀和
def get_presum(a):
    sum = list(accumulate(a))
    return sum

例题

蓝桥3382：区间次方和

遇到区间相关问题就应该联想到前缀和，本质是将区间问题转化为两个端点的问题。

提到区间还可以想到双指针，后续会进行更新。

import os
import sys

# 请在此输入您的代码
MOD = 1000000007 #模
def get_presum(a): #求前缀和
  n = len(a)
  sum = [0] * n
  sum[0] = a[0] #对各个变量及数组初始化
  for i in range(1,n):
    sum[i] = sum[i-1] + a[i]
  sum = [x % MOD for x in sum] #列表推导式（对sum前缀和数组每个元素进行求模）
  return sum

def get_sum(sum,l,r): #获得区间元素的和（al+al+1+...ar）
  if l == 0:
    return sum[r] #区间左端点特殊处理，因为python索引是有负数的，容易出错。
  else:
    return (sum[r] - sum[l-1] + MOD) % MOD

n, m = map(int, input().split())
a = list(map(int, input().split())) #读取数据

sum_list = []
for i in range(1,6): #遍历1-5（也就是次方的范围）
  tmp_a = [x ** i for x in a] #列表推导式，将a的每个元素变为i次方，并存储在tmp_a中。
  sum_list.append(get_presum(tmp_a)) #sum_list（存储每个次方前缀和数组，方便后续区间计算）

for _ in range(m): #查询m次
  l, r, k = map(int, input().split())   #读取左端点和右端点，次方数
  print(get_sum(sum_list[k - 1], l - 1, r - 1)) #题目下标从1开始，记得减去1

蓝桥3419小郑的蓝桥平衡串

将L、Q转换成数字，例如L为+1、Q为-1，问题就变成求区间和为0的最长区间

import os
import sys

# 请在此输入您的代码

def get_presum(a): #依旧是经典前缀和模板
  n = len(a)
  sum = [0] * n
  sum[0] = a[0]
  for i in range(1,n):
    sum[i] = sum[i - 1] + a[i]
  return sum

def get_sum(sum,l,r):
  if l == 0:
    return sum[r]
  else:
    return sum[r] - sum[l - 1]

a = input() #读取字符串
n = len(a) 
b = [] 
ans = 0 #初始化变量
left, right = 0, len(a) - 1 #左端点，右端点
for char in a: #遍历字符串a，将每个字符遍历
  if char == 'L': #如果是L，b列表添加一个值为1的元素
    b.append(1)
  else: #如果是Q，b列表添加一个值为-1的元素 #将l，q进行数字化，方便进行前缀和求区间元素之和
    b.append(-1)

sum = get_presum(b)
for l in range(n): #遍历左端点
  for r in range(l,n): #遍历右端点，寻找子串
    if get_sum(sum,l,r) == 0: #如果子串前缀和为0，则L，Q数量相等，平衡。
      ans = max(ans, r - l + 1) #更新答案
print(ans)

二维前缀和

概念

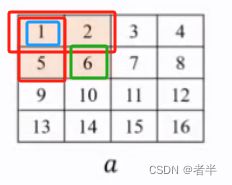
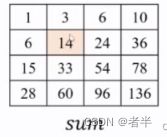
当前元素前缀和等于当前元素左上角的方阵内的元素之和。

二维前缀和会构造出一个新的前缀和矩阵，也就是二维数组，在python中就是二维列表。

面积推导公式

下标统一为从1开始，从0开始比较麻烦。

前缀和第i行第j列元素与上一行/上一列的元素，aij有什么关系呢？

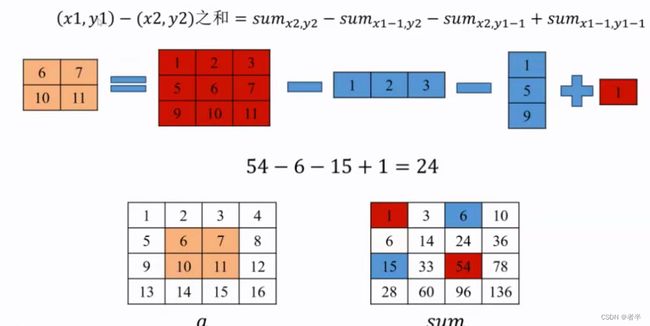
用面积来看，6是不是代表第一个a矩阵竖着的矩形面积，也就是sum[2][1],3同理代表第一个a矩阵横着的矩形面积，也就是sum[1][2],而我们求的是sum[2][2]，按面积来算是不是正方形的面积，而正方形的面积就是红色的两个长方形面积之和-蓝色正方形之和+绿色正方形之和。

• 想一下，矩阵的面积怎么确定，是不是可以转换为左上角坐标和右上角坐标，两个坐标就可以确定一个矩形。也就是又将区间问题转化为端点问题，这个思想我们是经常用到的，简化问题的思想。
• 其本质还是容斥定理。（可以用高中的交集并集来做联系）

• 其实也很好记忆，求sum各个元素也就是等于左边的元素+上边的元素-左上角的元素+本身aij

重点来了，怎么去计算区间元素之和呢，也许这边应该叫做矩阵元素之和，为了和一维前缀和取得联系，姑且这么取名。

用刚刚的矩形面积来进行推导。

• 这里得公式也很好记忆，也就是当前右下角的坐标不用动，而左上角的坐标记得-1（因为左上角的坐标是算在待求矩阵区间之和里的）再加上两个矩形的交集，也就是左上角坐标再往左上角。

我们也看一道例题：

蓝桥2109 统计子矩阵

具体代码如下

n, m, k = map(int,input().split())
#下标从1开始 
a= [[0] * (m +1) for i in range(n + 1)]
sum =[[0] * (m + 1) for i in range(n + 1)]
#输人一个二维数组
for i in range(1,n + 1):
    a[i] = [0] + list(map(int,input().split())) #假设读取列表[1,2,3],经过操作后就变[0,1,2,3]
for i in range(1,n + 1):
    for j in range(1, m + 1):
        sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j] #求前缀和公式
def get_sum(sum,x1,y1,x2,y2):
  return sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1] #求区间和
ans = 0
#遍历子矩阵
for x1 in range(1, n + 1): #左上角坐标
  for y1 in range(1, m + 1): 
    for x2 in range(x1, n + 1): #右下角坐标
      for y2 in range(y1, m + 1):
        if get_sum(sum,x1,y1,x2,y2) <= k: #如果满足条件
          ans += 1 #更新答案
print(ans)

总结：

做题方法：

1.套用模板求前缀和

2.对前缀和数组进行处理，求出区间元素之和。（要想清楚转化为端点问题）

3.遍历端点，进行求解

4.如果满足条件，更新答案

---

warning：记得关注数据下标从哪开始