代码随想录算法训练营第三十七天| 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯

文档讲解：代码随想录

视频讲解：代码随想录B站账号

状态：看了视频题解和文章解析后做出来了

动态规划理论基础

动态规划可以解决的问题一般都可以被拆分成小问题。区别于贪心，动规的当前状态一定是从之前的状态推导过来的，而贪心状态间是没有依赖关系的。

动态规划五部曲：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

Debug时的灵魂三问：

• 这道题目我举例推导状态转移公式了么？
• 我打印dp数组的日志了么？
• 打印出来了dp数组和我想的一样么？

509. 斐波那契数

维护一个长度等于n的数组

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n

        dp = [0 for _ in range(n+1)]
        dp[1] = 1

        for i in range(2, n+1):
            dp[i] = dp[i-1] + dp[i-2]

        return dp[n]

• 时间复杂度：O(n)
• 空间复杂度：O(n)

维护一个长度等于2的数组

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n

        dp = [0, 1]
        for i in range(2, n+1):
            sum = dp[0] + dp[1]
            dp[0] = dp[1]
            dp[1] = sum

        return dp[1]

• 时间复杂度：O(n)
• 空间复杂度：O(1)

动态规划五部曲：

1. 确定dp数组以及下标的含义：dp[i]为第i个斐波那契数字的值

2. 确定递推公式：题目已经给到 dp[i] = dp[i-1] + dp[i-2]

3. dp数组初始化：题目也已经给到，dp[0] = 0  dp[1] = 1

4. 确定遍历顺序：根据递推公式得知，第i个斐波那契数字需要它前两个数字来确定，所以一定是从前往后遍历

5. 举例推导dp数组：

N=10, 0 1 1 2 3 5 8 13 21 34 55

上面的两种方法，第二种是对第一种空间上的优化，我们只需要维护前两个斐波那契数列就可以无限推导出后面的，所以它的空间复杂度从O(n)下降到O(1).

70. 爬楼梯

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1 or n == 0:
            return 1

        prev1, prev2 = 2, 1

        for i in range(3, n+1):
            temp = prev1
            prev1 = prev1 + prev2
            prev2 = temp
        
        return prev1

• 时间复杂度：O(n)
• 空间复杂度：O(1)

动态规划五部曲：

1. 确定dp数组以及下标的含义：dp[i]为上到第i个台阶的方法数量

2. 确定递推公式：有两种方式上到第i个台阶dp[i]

（1）从dp[i-1]迈一步

（2）从dp[i-2]迈两步

所以dp[i] = dp[i-1] + dp[i-2]

3. dp数组初始化：大多数人都会很纠结dp[0]的初始化应该是0还是1，其实两种初始化的方式都能找到理由，但在此题中，其实第0个台阶是没有意义的，因为题目设定n是正整数。

所以只需要弄清楚dp[1]和dp[2]的初始化然后从dp[3]开始遍历就好

dp[1] = 1; dp[2] = 2

4. 确定遍历顺序：根据递推公式得知需要从前往后遍历

5. 举例推导dp数组：

N=5, 1 2 3 5 8，就是斐波那契数列。

746. 使用最小花费爬楼梯

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        if len(cost) <= 2:
            return min(cost)

        dp = [float('inf') for _ in range(len(cost) + 1)]
        dp[0] = 0
        dp[1] = 0

        for i in range(2, len(cost) + 1):
            dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i-1])
        return dp[len(cost)]

• 时间复杂度：O(n)
• 空间复杂度：O(n)

动态规划五部曲：

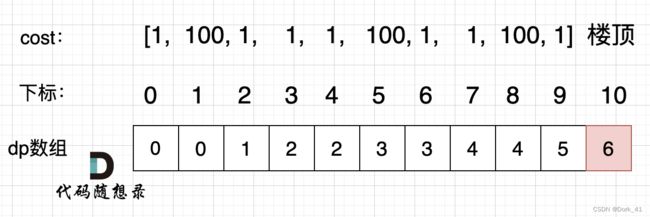
1. 确定dp数组以及下标的含义：dp[i]到达第i个台阶时的最小花费

2. 确定递推公式：到当前台阶的最小花费是到达i-1和i-2台阶的最小花费加上i-1和i-2本身台阶的花费，取它们的较小值，dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i-1])

3. dp数组初始化：到达台阶0和台阶1的花费为0，因为可以这里出发

4. 确定遍历顺序：根据递推公式得知，第i个斐波那契数字需要它前两个数字来确定，所以一定是从前往后遍历

5. 举例推导dp数组：