机器学习-63-Structured Learning-04-Sequence Labeling Problem(结构化学习-序列标注(HMM,CRF))
文章目录
-
- Sequence Labeling Problem
-
- Sequence Labeling
-
- Definition
- Application
- Example Task:POS tagging
- Outline(大纲)
- HMM
-
- 介绍
- 什么样的问题需要HMM模型
- How you generate a sentence?
-
- step 1
- step 2
- HMM的数学表达
- Estimating the probabilities(概率估计)
- How to do POS Tagging?(如何进行词性标记)
- Viterbi Algorithm(维特比算法)
- Summary(总结)
- Drawbacks(缺点)
- Conditional Random Field (CRF,条件随机场)
-
- P(x,y) for CRF
- Feature Vector
- Training Criterion
- Inference
- CRF vs HMM
-
- Synthetic Data(合成数据)
- Summary
- Structured Perceptron/SVM
-
- Structured Perceptron
- Structured Perceptron vs CRF
- Structured SVM
- Structured SVM – Error Function
- 不同方法的比较
- 为什么不用RNN
- 把传统方法和深度学习整合在一起
- Concluding Remarks
Sequence Labeling Problem
上一章节我们讲到结构化学习的一种方法—结构化支持向量机,本章学习另一种结构化学习的方法—序列标注。
Sequence Labeling
Definition
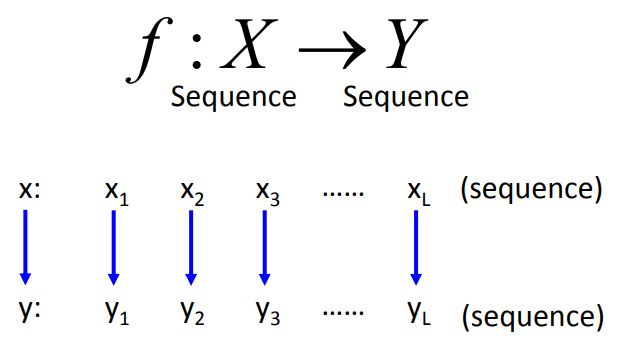
f : X → Y f : X \rightarrow Y f:X→Y
序列标注的问题可以理解为:机器学习所要寻找的目标函数的输入是一个序列,输出也为一个序列,并且假设输入输出的序列长度相同,即输入可以写成序列向量的形式,输出也为序列向量。该任务可以利用循环神经网络来解决,但本章节我们可以基于结构化学习的其它方法进行解决(两步骤,三问题)。
Application

命名实体识别:就是给定一个句子来识别这个句子中的人名,地名,组织名称等信息
比如:
-
给定一个句子:“Harry Potter is a student of Hogwarts and lived on Privet Drive.”
就可以得出:Harry Potter是人名,Hogwarts 是组织名,Privet Drive是人名
但是对于中文的抽取很麻烦,例如下面两句要抽取人名:
- 楊 公 再 興 之 神
- 馮 氏 埋 香 之 塚
Example Task:POS tagging
POS tagging:标记一个句子中每个word的词性。
词性有很多的类别,名词下面就可以分成proper(专有名词 )、common(一般名词)。动词可以分成main(主动词),modals(情态动词)等等。

现在要做的就是输入一个句子(比如,John saw the saw),系统将会标记John为专有名词,saw为动词,the为限定词,saw为名词;
词性标注是自然语言处理中非常典型和重要的task,是许多文字理解的基石,比如要先有词性标注,后续才能比较方便地做句法分析和词义消歧,或者抽key word(一般是名词),自动检测出哪些词汇是名词的话,就可以先去掉一些不可能的词汇。

如果今天找到一个字典,告诉我们说每个词汇的词性是什么,那不就解决词性标注的问题了吗?写一个hash table,hash table告诉我们说“the”的output是“D",那词性标注的问题不就解决了吗?这里困难的点是,词性标注光靠查表是不够的,要知道一整个sequence的信息才有可能把每一个word的词性找出来。
- 第一个"saw"更有可能是动词V,而不是名词N;
- 然而,第二个"saw"是名词N,因为名词N更可能跟在冠词“the”后面。
所以要把词性标注做好的话,必须考虑整个sequence的信息。
Outline(大纲)

HMM
介绍
隐马尔科夫模型(Hidden Markov Model,以下简称HMM)是比较经典的机器学习模型了,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。当然,随着目前深度学习的崛起,尤其是RNN,LSTM等神经网络序列模型的火热,HMM的地位有所下降。但是作为一个经典的模型,学习HMM的模型和对应算法,对我们解决问题建模的能力提高以及算法思路的拓展还是很好的。本文是HMM系列的第一篇,关注于HMM模型的基础。
什么样的问题需要HMM模型
首先我们来看看什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征:
- 我们的问题是基于序列的,比如时间序列,或者状态序列。
- 们的问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。
有了这两个特征,那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。比如:我现在在打字写博客,我在键盘上敲出来的一系列字符就是观测序列,而我实际想写的一段话就是隐藏序列,输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话,并把最可能的词语放在最前面让我选择,这就可以看做一个HMM模型了。再举一个,我在和你说话,我发出的一串连续的声音就是观测序列,而我实际要表达的一段话就是状态序列,你大脑的任务,就是从这一串连续的声音中判断出我最可能要表达的话的内容。
从这些例子中,我们可以发现,HMM模型可以无处不在。但是上面的描述还不精确,下面我们用精确的数学符号来表述我们的HMM模型。
How you generate a sentence?

我们如何生成一个句子呢?
这里主要是两个步骤:
step1:
当你想要说一句话的时候,你第一件在心里做的事情是先产生一个POS sequence,这个sequence是根据你脑中的grammar产生的(你大脑中对人类语言的理解)。
step2:
根据每一个tag(PN、V、D、N),去找一个符合tag的词汇,变成一个word sequence。文字和词性的关系可以从一个词典中得到。
step 1
当你想要说一句话的时候,你第一件在心里做的事情是先产生一个POS sequence,这个sequence是根据你脑中的grammar产生的(你大脑中对人类语言的理解)。
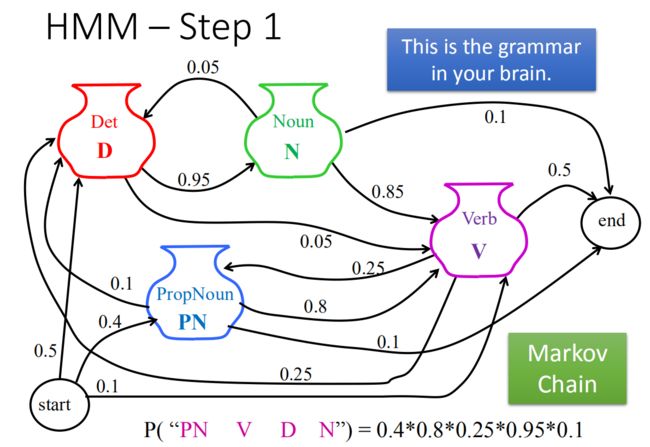
实际上这就是一个马尔科夫链,例如:
要说一句话,放在句首的0.5的几率是冠词,0.4的几率是专有名词,0.1的几率是动词
这里随机sample一下,假设第一个词是专有名词PN,PN后面80%几率是动词V,10%几率是冠词,10%几率直接结束。然后再随机sample一下。一直往下,直到end。
注意:每一个词后面接什么词合起来的几率应该是1,不是1就是ppt有问题。
当我们要计算"PN V D N"这样的一个序列的概率:
P ( " P N V D N " ) = 0.4 × 0.8 × 0.25 × 0.95 × 0.1 P("PN \ \ \ V\ \ \ D \ \ \ N") = 0.4 × 0.8 × 0.25 × 0.95 ×0.1 P("PN V D N")=0.4×0.8×0.25×0.95×0.1
step 2
根据我们脑袋中的词典,把相应的词根据词性放到相应位置。
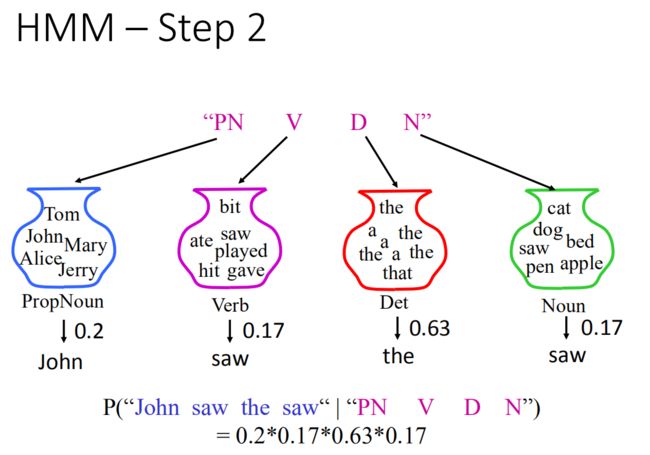
根据每一个tag(PN、V、D、N),在词典中找一个符合tag的词汇,变成一个word sequence。
名词罐子里面有五个词,sample出John的几率是0.2,同理:得到saw的几率是0.17,the的几率是0.63,最后saw的几率是0.17,根据词性这句话出现的几率为:
P ( " J o h n s a w t h e s a w " ∣ " P N V D N " ) = 0.2 × 0.17 × 0.63 × 0.17 P("John \ \ saw \ \ the \ \ saw"|"PN \ \ V \ \ D \ \ N") = 0.2×0.17×0.63×0.17 P("John saw the saw"∣"PN V D N")=0.2×0.17×0.63×0.17
HMM的数学表达

HMM实际上就是在描述下面这件事情:
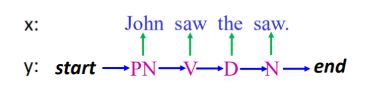
数学表达为:
P ( x , y ) = P ( y ) P ( x ∣ y ) P(x,y) = P(y)P(x|y) P(x,y)=P(y)P(x∣y)
来看看右边分别怎么算的:
P ( y ) = P ( P N ∣ s t a r t ) × P ( V ∣ P N ) × P ( D ∣ V ) × P ( N ∣ D ) P(y) = P(PN|start)×P(V|PN)×P(D|V)×P(N|D) P(y)=P(PN∣start)×P(V∣PN)×P(D∣V)×P(N∣D)
P ( x ∣ y ) = P ( J o h n ∣ P N ) × P ( s a w ∣ V ) × P ( t h e ∣ D ) × P ( s a w ∣ N ) P(x|y) = P(John|PN)×P(saw|V)×P(the|D)×P(saw|N) P(x∣y)=P(John∣PN)×P(saw∣V)×P(the∣D)×P(saw∣N)
用更加一般化的数学表达HMM:

输入: x = x 1 , x 2 ⋯ x L x=x_{1}, x_{2} \cdots x_{L} x=x1,x2⋯xL
输出: y = y 1 , y 2 ⋯ y L y=y_{1}, y_{2} \cdots y_{L} y=y1,y2⋯yL
-
Step1 计算y的概率就是各个词性出现的条件概率积,这个条件概率称为
Transition probability(转移概率)
P ( y ) = P ( y 1 ∣ s t a r t ) × ∏ l = 1 L − 1 P ( y l + 1 ∣ y l ) × P ( e n d ∣ y L ) (1) P(y)=P\left(y_{1} | s t a r t\right)\times \prod_{l=1}^{L-1} P\left(y_{l+1} | y_{l}\right) \times P\left(e n d | y_{L}\right) \tag{1} P(y)=P(y1∣start)×l=1∏L−1P(yl+1∣yl)×P(end∣yL)(1) -
Step2 会计算x|y的概率,是词性产生word的条件概率积,这个条件概率称为
Emission probability(发散概率)
P ( x ∣ y ) = ∏ l = 1 L P ( x l ∣ y l ) (2) P(x | y)=\prod_{l=1}^{L} P\left(x_{l} | y_{l}\right) \tag{2} P(x∣y)=l=1∏LP(xl∣yl)(2)
写到一起:
P ( y ) = P ( y 1 ∣ s t a r t ) × ∏ l = 1 L − 1 P ( y l + 1 ∣ y l ) × P ( e n d ∣ y L ) × ∏ l = 1 L P ( x l ∣ y l ) (3) P(y)=P\left(y_{1} | s t a r t\right)\times \prod_{l=1}^{L-1} P\left(y_{l+1} | y_{l}\right) \times P\left(e n d | y_{L}\right) × \prod_{l=1}^{L} P\left(x_{l} | y_{l}\right) \tag{3} P(y)=P(y1∣start)×l=1∏L−1P(yl+1∣yl)×P(end∣yL)×l=1∏LP(xl∣yl)(3)
那么问题来了,怎么算这两个几率呢?
Estimating the probabilities(概率估计)

怎么算转移概率、发射概率?
这个就要从训练数据中得到,先收集一大堆的训练数据(sentence),每个sentence词汇都标注好词性了。每一个sentence就是一笔training data。

那么算公式(1)中的 P ( y l + 1 ∣ y l ) P(y_{l+1}|y_l) P(yl+1∣yl)这个概率就是计算:
P ( y l + 1 = s ′ ∣ y l = s ) ( s and s ′ are tags ) = count ( s → s ′ ) count ( s ) \frac{P\left(y_{l+1}=s^{\prime} | y_{l}=s\right)}{\left(s \text { and } s^{\prime} \text { are tags }\right)}=\frac{\operatorname{count}\left(s \rightarrow s^{\prime}\right)}{\operatorname{count}(s)} (s and s′ are tags )P(yl+1=s′∣yl=s)=count(s)count(s→s′)
s和s ′ 是tag(词性标签), c o u n t ( s ) count(s) count(s)就是在训练集中s出现的次数, c o u n t ( s → s ′ ) count(s\rightarrow s') count(s→s′)就是在训练集中s后面接s’的次数。
算公式(2)中的 P ( x l ∣ y l ) P\left(x_{l} | y_{l}\right) P(xl∣yl)这个概率就是计算:
P ( x l = t ∣ y l = s ) ( s is tag, and t is word ) = count ( s → t ) count ( s ) \frac{P\left(x_{l}=t | y_{l}=s\right)}{(s \text { is tag, and } t \text { is word })}=\frac{\operatorname{count}(s \rightarrow t)}{\operatorname{count}(s)} (s is tag, and t is word )P(xl=t∣yl=s)=count(s)count(s→t)
s是tag,t是word, P ( x l = t ∣ y i = s ) P(x_l=t|y_i=s) P(xl=t∣yi=s)的意思就是给一个词性,产生一个词汇的概率。 c o u n t ( s ) count(s) count(s)就是在训练集中s出现的次数, c o u n t ( s → t ) count(s\rightarrow t) count(s→t)在训练集中词性为s且词汇为t的次数。
讲到这里,老师解释了一下HMM在处理语音序列的时候表达式不是这样的,处理语音序列的时候,HMM里面的都是一个个高斯分布形成的GMM,不是像这里用统计的方法算出来的,GMM要用EM来解,这里不用。为什么?老师也没说,自己想。。。
How to do POS Tagging?(如何进行词性标记)
有两个上面算出来的概率之后,要做什么呢?
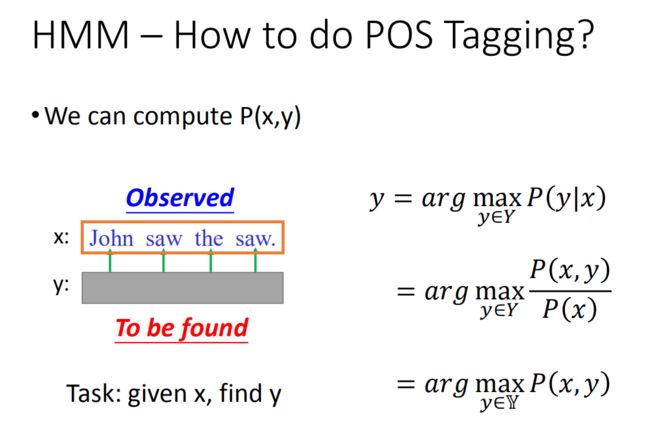
回到原来的问题,给一个句子x,要找y,x是我们看得到的,而y是隐藏的,这也就是为什么叫Hidden的原因!那找出y就要靠 P ( x , y ) P(x,y) P(x,y)
用概率来说就是,在给定x 的条件下出现的几率的y 就是我们要求的y:
y = arg max y ∈ Y P ( y ∣ x ) y = \arg \max\limits_{y\in Y} P(y|x) y=argy∈YmaxP(y∣x)
上式可以写成:
y = arg max y ∈ Y P ( x , y ) P ( x ) y = \arg \max\limits_{y\in Y} \frac{P(x,y)}{P(x)} y=argy∈YmaxP(x)P(x,y)
由于分母P ( x ) 是固定的,所以上式等价于:
y = arg max y ∈ Y P ( x , y ) y = \arg \max\limits_{y\in Y} P(x,y) y=argy∈YmaxP(x,y)
这个最有可能的y就是穷举所有的y,然后带入公式P ( x , y )里面,然后找到最大的那个~!,我们把它记为 y ~ \tilde{y} y~
下面来分析一下这个做法:
Viterbi Algorithm(维特比算法)

从前面我们可以知道给定一个x真正要求的是:
y ~ = arg max y ∈ Y P ( x , y ) \tilde{y} = \arg \max\limits_{y\in Y} P(x,y) y~=argy∈YmaxP(x,y)
如果是穷举所有可能的情况,那么假设现在有s个词性,sequnce长度是L,那有可能的y就是 s L s^L sL个!这个是非常大的数量。
但是用Viterbi Algorithm来解决这个问题,其算法时间复杂度为: O ( L S 2 ) O(LS^2) O(LS2)!
那么什么是Viterbi-Algorithm算法呢?
维特比算法是一个特殊但应用最广的动态规划算法。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图-篱笆网了(Lattice)的有向图最短路径问题而提出来的。它之所以重要,是因为凡是使用隐马尔科夫模型描述的问题都可以用它解码,包括当前的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
更多的就不介绍了,可以看这篇文章: Viterbi-Algorithm(维特比算法)
Summary(总结)
HMM的过程:

HMM也是结构化学习的一种方法,就要回答三个问题:
-
Q1:评估
F ( x , y ) = P ( x , y ) = P ( y ) P ( x ∣ y ) F(x, y)=P(x, y)=P(y) P(x | y) F(x,y)=P(x,y)=P(y)P(x∣y)
该评估函数可以理解为x与y的联合概率。 -
Q2:推理
y ~ = arg max y ∈ Y P ( x , y ) \tilde{y}=\arg \max _{y \in \mathbb{Y}} P(x, y) y~=argy∈YmaxP(x,y)
定一个x,求出最大的y,使得我们定义函数的值达到最大(即维特比算法)。 -
Q3:训练
从训练数据集中统计得到P(y)与P(x | y)
该过程就是计算几率的问题或是统计语料库中词频的问题。
Drawbacks(缺点)
HMM会有什么问题?

在做Q2推理的时候,我们是把让P(x,y)最大的y作为output:
y ~ = arg max y ∈ Y P ( x , y ) \tilde{y}=\arg \max _{y \in \mathbb{Y}} P(x, y) y~=argy∈YmaxP(x,y)
如果我们要让HMM得到正确的结果,我们会希望正确的 y ~ \tilde{y} y~ :
( x , y ^ ) : P ( x , y ^ ) > P ( x , y ) (x, \hat{y}) : P(x, \hat{y})>P(x, y) (x,y^):P(x,y^)>P(x,y)
但是HMM可以做到这件事情吗?
HMM可能无法做到这件事情,在HMM训练中,你会发现它并没有保证可以让错误的y的P(x,y)一定是小的。
可能你会很懵逼,我们这里举一个例子来说明一下:
假设从语料库中的数据是统计出来(如上图右边所示):
-
转移概率
- N后面接V的概率是9/10: P ( V ∣ N ) = 9 10 P(V|N) = \frac{9}{10} P(V∣N)=109
- N后面接D的概率是1/10: P ( D ∣ N ) = 1 10 P(D|N) = \frac{1}{10} P(D∣N)=101
-
分散概率
- V词性是word a的概率是1/2: P ( a ∣ V ) = 1 2 P(a|V) = \frac{1}{2} P(a∣V)=21
- V词性是word c的概率是1/2: P ( c ∣ V ) = 1 2 P(c|V) = \frac{1}{2} P(c∣V)=21
- D词性是word a的概率是1: P ( a ∣ D ) = 1 P(a|D) = 1 P(a∣D)=1
可以看到,每一种词性的转移概率和发散概率各自的总和是1!

假设我们知道在 l − 1 l-1 l−1时刻词性标记为N,即 y l − 1 = N \mathrm{y}_{\mathrm{l}-1}=\mathrm{N} yl−1=N,在 l l l 时刻我们看到的单词为a,现在需要求出 y l = ? y_{l}=? yl=?即 y l y_l yl最有可能的词性是什么?
根据我们之前得到的概率,我们可以得到:
- y l = V y_l = V yl=V的概率为0.9 × 0.5 = 0.45
- y l = D y_l = D yl=D的概率为0.1 × 1 = 0.1
所以最有可能的词性是V
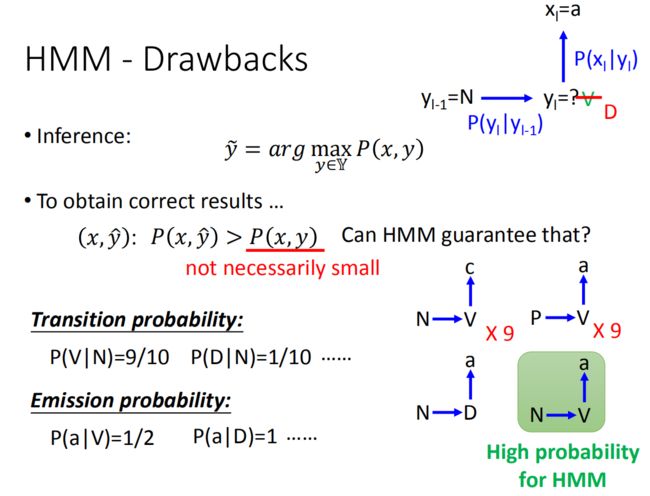
可是如果我们观察下训练数据(如上图右边所示,和我们前面看的不同之处在于加了状态P,但其他的跟前面讲的概率相同), N → V → c N→V→c N→V→c出现9次, P → V → a P→V→a P→V→a出现9次, N → D → a N→D→a N→D→a出现1次,那么N后面接V的概率是0.9,N后面接D的概率是0.1。V产生a的概率是0.5,产生c的概率是0.5,D产生a的概率是1。
根据训练数据,告诉我们说是V,但是你不觉得有问题吗?
在训练数据里,已经告诉你 N → D → a N→D→a N→D→a,但是你还是预测为V,这不是很奇怪吗。
对HMM来说,它会给一些在训练数据里没出现过的sequence高的概率(例如上面例子的 N → D → a N→D→a N→D→a)。
也就是说HMM算法只会按照概率的高低来进行估计,并不管这个序列是否出现过(HMM自己脑补了未出现过的东西)。
但这个脑补的过程也不能说就是个坏事:

由于训练数据很少,也就是意味在真实的数据中是有可能出现训练数据中没有出现过的序列的,因此HMM在训练数据很少的时候性能反而比较好。也就是说训练数据多的时候HMM的表现并没有比较好。
隐马尔可夫模型会产生未卜先知的情况,是因为转移概率(Transition probability)和发散概率(Emission probability),在训练时是分开建模的,两者是相互独立的。因此解决这个现象就是用更加复杂的模型,把这两个东西都考虑起来,即我们也可以用一个更复杂的模型来模拟两个序列之间的可能性,但要避免过拟合!
下面要讲的CRF就是用同样的模型,解决这个问题。
Conditional Random Field (CRF,条件随机场)

CRF描述的也是P(x, y)的问题,但与条件随机场表示形式很不一样(本质上是在训练阶段不同),其几率正比于 e x p ( w ⋅ ϕ ( x , y ) ) exp(w\cdot ϕ(x,y)) exp(w⋅ϕ(x,y)):
P ( x , y ) ∝ exp ( w ⋅ ϕ ( x , y ) ) (1) \mathrm{P}(x, y) \propto \exp (w \cdot \phi(x, y)) \tag{1} P(x,y)∝exp(w⋅ϕ(x,y))(1)
- ϕ ( x , y ) ϕ(x,y) ϕ(x,y)为一个特征向量;
- w是一个权重向量,可以从训练数据中学习得到;
- e x p ( w ⋅ ϕ ( x , y ) ) exp(w \cdot ϕ(x,y)) exp(w⋅ϕ(x,y))总是正的,
可以大于1。所以说是概率的话就不太对,只能说和概率是成正比的。
那我们不就不知道真正的P(x,y)是什么了吗?
没关系,CRF不关心P(x,y),真正关心的是P(y|x):
P ( y ∣ x ) = P ( x , y ) ∑ y ′ P ( x , y ′ ) (2) P(y | x)=\frac{P(x, y)}{\sum_{y^{\prime}} P\left(x, y^{\prime}\right)} \tag{2} P(y∣x)=∑y′P(x,y′)P(x,y)(2)
由公式(1)的正比可以得到:
P ( x , y ) = exp ( w ⋅ ϕ ( x , y ) ) R (3) P(x,y) = \frac{\exp (w \cdot \phi(x, y))}{R} \tag{3} P(x,y)=Rexp(w⋅ϕ(x,y))(3)
公式(2)的分母部分我们也可以得出:
∑ y ′ P ( x , y ′ ) = ∑ y ′ ∈ Y exp ( w ⋅ ϕ ( x , y ′ ) ) R (4) \sum_{y\prime}P(x,y\prime) = \sum_{y\prime\in Y}\frac{\exp (w \cdot \phi(x, y\prime))}{R} \tag{4} y′∑P(x,y′)=y′∈Y∑Rexp(w⋅ϕ(x,y′))(4)
将公式(3)和公式(4)带入公式(2):
P ( y ∣ x ) = exp ( w ⋅ ϕ ( x , y ) ) R ∑ y ′ ∈ Y exp ( w ⋅ ϕ ( x , y ′ ) ) R = exp ( w ⋅ ϕ ( x , y ) ) ∑ y ′ ∈ Y exp ( w ⋅ ϕ ( x , y ′ ) ) (5) P(y | x)=\frac{\frac{\exp (w \cdot \phi(x, y))}{R}}{\sum_{y\prime\in Y}\frac{\exp (w \cdot \phi(x, y\prime))}{R} } = \frac{\exp (w \cdot \phi(x, y))}{\sum_{y\prime\in Y}\exp (w \cdot \phi(x, y\prime)) } \tag{5} P(y∣x)=∑y′∈YRexp(w⋅ϕ(x,y′))Rexp(w⋅ϕ(x,y))=∑y′∈Yexp(w⋅ϕ(x,y′))exp(w⋅ϕ(x,y))(5)
分母中是对所有的y进行求和,因此和x是相互独立的,可以把公式(5)写成:
P ( y ∣ x ) = exp ( w ⋅ ϕ ( x , y ) ) Z ( x ) P(y|x) = \frac{\exp (w \cdot \phi(x, y))}{Z(x)} P(y∣x)=Z(x)exp(w⋅ϕ(x,y))
P(x,y) for CRF
你可能会奇怪,为什么概率会正比于两个向量的内积,跟HMM完全不一样呀!
emm…其实是一样的!
为什么说CRF和HMM是一样的呢?是有人证明了的,CRF只不过是training上不一样,我们来看,在HMM里面是这样计算P ( x , y ) 的:
P ( x , y ) = P ( y 1 ∣ s t a r t ) ∏ l = 1 L − 1 P ( y l + 1 ∣ y l ) P ( e n d ∣ y L ) ∏ l = 1 L P ( x l ∣ y l ) (1) P(x, y)=P\left(y_{1} | s t a r t\right) \prod_{l=1}^{L-1} P\left(y_{l+1} | y_{l}\right) P\left(e n d | y_{L}\right) \prod_{l=1}^{L} P\left(x_{l} | y_{l}\right) \tag{1} P(x,y)=P(y1∣start)l=1∏L−1P(yl+1∣yl)P(end∣yL)l=1∏LP(xl∣yl)(1)
按乘法变加法的套路,对公式(1)的两边取对数
log P ( x , y ) = log P ( y 1 ∣ star t ) + ∑ l = 1 L − 1 log P ( y l + 1 ∣ y l ) + log P ( end ∣ y L ) + ∑ l = 1 L log P ( x l ∣ y l ) (2) {\log P(x, y)} {=\log P\left(y_{1} | \operatorname{star} t\right)+\sum_{l=1}^{L-1} \log P\left(y_{l+1} | y_{l}\right)+\log P\left(\text {end} | y_{L}\right)} {\quad+\sum_{l=1}^{L} \log P\left(x_{l} | y_{l}\right)} \tag{2} logP(x,y)=logP(y1∣start)+l=1∑L−1logP(yl+1∣yl)+logP(end∣yL)+l=1∑LlogP(xl∣yl)(2)

我们先来看一下上面红色方框的部分,把这一项做下整理就得到了:
∑ l = 1 L log P ( x l ∣ y l ) = ∑ s , t l o g P ( t ∣ s ) × N s , t ( x , y ) \sum_{l=1}^{L} \log P\left(x_{l} | y_{l}\right) = \sum_{s,t}logP(t|s) \times N_{s,t}(x,y) l=1∑LlogP(xl∣yl)=s,t∑logP(t∣s)×Ns,t(x,y)
-
∑ l = 1 L \sum_{l=1}^{L} ∑l=1L穷举所有可能的标记s和所有可能的单词t;
-
log P ( x l ∣ y l ) \log P\left(x_{l} | y_{l}\right) logP(xl∣yl)表示给定标记s的单词取对数的形式;
-
N s , t ( x , y ) N_{s, t}(x, y) Ns,t(x,y)表示为单词t被标记成s的事情,在(x, y)对中总共出现的次数。
如果有10个可能的词性(s=10)和10000个词汇(t=10000),那这里就是summation ∑ s , t = 10 ∗ 10000 \sum_{s,t} = 10*10000 ∑s,t=10∗10000 项。
可能有点难理解,这里对于上面的转换再举一个具体的例子吧:

举个例子:有一个sentence x “The dog ate the homework”,每一个word都有一个tag的label。
x : T h e d o g a t e t h e h o m e w o r k y : D N V D N \begin{aligned} & x: The \ dog \ ate \ the \ homework \\ & y:\ D \ \ \ \ \ N\ \ \ V\ \ \ D\ \ \ \ \ \ \ \ \ \ \ \N \end{aligned} x:The dog ate the homeworky: D N V D N
我们来分别计算每一个pair (x, y)出现的次数(不考虑大小写):
- “the”被标记为D(冠词),这个(x,y) pair出现的次数为2次: N D , t h e ( x , y ) = 2 N_{D,the}(x,y) = 2 ND,the(x,y)=2
- “dog”被标记为N(名词)的次数为1次: N N , d o g ( x , y ) = 1 N_{N,dog}(x,y) = 1 NN,dog(x,y)=1
- “ate”被标记为V(动词)的次数为1次: N V , a t e ( x , y ) = 1 N_{V,ate}(x,y)=1 NV,ate(x,y)=1
- “homework”被标记为N(名词)的次数为1次: N N , h o m e w o r k ( x , y ) = 1 N_{N,homework}(x,y) = 1 NN,homework(x,y)=1
- 其他词汇和词性的次数为0次: N s , t ( x , y ) = 0 N_{s,t}(x,y) = 0 Ns,t(x,y)=0
计算下所有的概率的乘积:
∑ l = 1 L log P ( x l ∣ y l ) = log P ( the ∣ D ) + log P ( dog ∣ N ) + log P ( ate ∣ V ) + log P ( the ∣ D ) + log P ( homework ∣ N ) = log P ( the ∣ D ) × 2 + log P ( dog ∣ N ) × 1 + log P ( a t e ∣ V ) × 1 + log P ( homework ∣ N ) × 1 \begin{aligned} \sum_{l=1}^{L} \log P\left(x_{l} | y_{l}\right) & {=\log P(\text {the} | D)+\log P(\operatorname{dog} | N)+\log P(\text {ate} | V)} {+\log P(\text {the} | D)+\log P(\text {homework} | N)} \\ & = {\log P(\text { the } | D) \times 2+\log P(\operatorname{dog} | N) \times 1+\log P(a t e | V) \times 1} {+\log P(\text {homework} | N) \times 1} \end{aligned} l=1∑LlogP(xl∣yl)=logP(the∣D)+logP(dog∣N)+logP(ate∣V)+logP(the∣D)+logP(homework∣N)=logP( the ∣D)×2+logP(dog∣N)×1+logP(ate∣V)×1+logP(homework∣N)×1
可以看到,我们对概率对数之和整理之后,其实就可以得到下列等式:
∑ l = 1 L log P ( x l ∣ y l ) = ∑ s , t l o g P ( t ∣ s ) × N s , t ( x , y ) (3) \sum_{l=1}^{L} \log P\left(x_{l} | y_{l}\right) = \sum_{s,t}logP(t|s) \times N_{s,t}(x,y) \tag{3} l=1∑LlogP(xl∣yl)=s,t∑logP(t∣s)×Ns,t(x,y)(3)
对于公式(2)的其他项我们也可以做一样的转化:

其中:
-
第一项:
log P ( y 1 ∣ s t a r t ) = ∑ s log P ( s ∣ s t a r t ) × N s t a r t , x ( x , y ) (4) \log P(y_1|start) = \sum_s\log P(s|start)\times N_{start,x}(x,y) \tag{4} logP(y1∣start)=s∑logP(s∣start)×Nstart,x(x,y)(4)
表示对所有标记的词性s放在句首的几率取对数,再乘上在(x, y)对中,标记s放在句首所出现的次数。 -
第二项:
∑ l = 1 L − 1 log P ( y l + 1 ∣ y l ) = ∑ s , s ′ log P ( s ′ ∣ s ) × N s , s ′ ( x , y ) (5) \sum_{l=1}^{L-1} \log P\left(y_{l+1} | y_{l}\right)=\sum_{s, s^{\prime}} \log P\left(s^{\prime} | s\right) \times N_{s, s^{\prime}}(x, y) \tag{5} l=1∑L−1logP(yl+1∣yl)=s,s′∑logP(s′∣s)×Ns,s′(x,y)(5)
表示计算s后面的标记后面跟s’在(x, y)里面所出现的次数,再乘上s后面跟s’的几率取对数。 -
第三项:
log P ( end ∣ y L ) = ∑ s log P ( e n d ∣ s ) × N s , end ( x , y ) (6) \log P\left(\text {end} | y_{L}\right)=\sum_{s} \log P(e n d | s) \times N_{s, \text {end}}(x, y) \tag{6} logP(end∣yL)=s∑logP(end∣s)×Ns,end(x,y)(6)
表示对所有标记的词性s放在句尾的几率取对数,再乘上在(x, y)对中,标记s放在句尾所出现的次数。

将我们上面推导得到的公式(3),(4),(5),(6)带进公式(2):
log P ( x , y ) = log P ( y 1 ∣ star t ) + ∑ l = 1 L − 1 log P ( y l + 1 ∣ y l ) + log P ( end ∣ y L ) + ∑ l = 1 L log P ( x l ∣ y l ) (2) {\log P(x, y)} {=\log P\left(y_{1} | \operatorname{star} t\right)+\sum_{l=1}^{L-1} \log P\left(y_{l+1} | y_{l}\right)+\log P\left(\text {end} | y_{L}\right)} {\quad+\sum_{l=1}^{L} \log P\left(x_{l} | y_{l}\right)} \tag{2} logP(x,y)=logP(y1∣start)+l=1∑L−1logP(yl+1∣yl)+logP(end∣yL)+l=1∑LlogP(xl∣yl)(2)
中,就可以得到:
log P ( x , y ) = ∑ s , t log P ( t ∣ s ) × N s , t ( x , y ) + ∑ s log P ( s ∣ start ) × N start , s ( x , y ) + ∑ s , s ′ log P ( s ′ ∣ s ) × N s , s ′ ( x , y ) + ∑ s log P ( e n d ∣ s ) × N s , e n d ( x , y ) (7) \begin{aligned} {\log P(x, y)} = & \sum_{s, t} \log P(t | s) \times N_{s, t}(x, y) {+\sum_{s} \log P(s | \text {start}) \times N_{\text {start}, s}(x, y)} \\ & {+\sum_{s, s^{\prime}} \log P\left(s^{\prime} | s\right) \times N_{s, s^{\prime}}(x, y)}+\sum_{s} \log P(e n d | s) \times N_{s, e n d}(x,y) \end{aligned} \tag{7} logP(x,y)=s,t∑logP(t∣s)×Ns,t(x,y)+s∑logP(s∣start)×Nstart,s(x,y)+s,s′∑logP(s′∣s)×Ns,s′(x,y)+s∑logP(end∣s)×Ns,end(x,y)(7)
其实看我们上面的式子,我们可以发现四项中每一个其实都是两个数相乘然后相加:
- summation over所有的tag跟word
- summation over所有的tag
- summation over所有的tag和tag
- summation over所有的tag
最后四项求和。那么近一步我们就可以将公式(7)描述成两个向量的inner product:
log P ( x , y ) = [ ⋮ log P ( t ∣ s ) ⋮ ⋮ log P ( s ∣ s t a r t ) ⋮ log P ( s ′ ∣ s ) ⋮ log P ( e n d ∣ s ) ⋮ ] ⋅ [ ⋮ N s , t ( x , y ) ⋮ ⋮ N start , s ( x , y ) ⋮ N s , s ′ ( x , y ) ⋮ N s , e n d ( x , y ) ⋮ ] (8) \log P(x, y) =\left[\begin{array}{c}{\vdots} \\ {\log P(t | s)} \\ {\vdots} \\ {\vdots} \\ {\log P(s | s t a r t)} \\ {\vdots} \\ {\log P\left(s^{\prime} | s\right)} \\ {\vdots} \\ {\log P(e n d | s)} \\ {\vdots}\end{array}\right]\cdot \left[\begin{array}{c}{\vdots} \\ {N_{s, t}(x, y)} \\ {\vdots} \\ \vdots \\ {N_{\text {start}, s}(x, y)} \\ {\vdots} \\ {N_{s, s^{\prime}}(x, y)} \\ {\vdots} \\ {N_{s, e n d}(x, y)} \\ \vdots \end{array}\right] \tag{8} logP(x,y)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡⋮logP(t∣s)⋮⋮logP(s∣start)⋮logP(s′∣s)⋮logP(end∣s)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⋅⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡⋮Ns,t(x,y)⋮⋮Nstart,s(x,y)⋮Ns,s′(x,y)⋮Ns,end(x,y)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(8)
进而可以用 w ⋅ ϕ ( x , y ) w\cdot ϕ(x,y) w⋅ϕ(x,y)表示,第二个向量是依赖于(x, y)的,是(x,y)所形成的Feature,写成 ϕ ( x , y ) \phi(x,y) ϕ(x,y)。
对公式(8)两边同时取指数e:
P ( x , y ) = e x p ( w ⋅ ϕ ( x , y ) ) P(x,y) = exp(w\cdot \phi(x,y)) P(x,y)=exp(w⋅ϕ(x,y))
到这里就从HMM的形式推导到CRF的形式了,说明两个是一码事,但是注意,在CRF的定义中,上面的式子不是等号是正比于 ∝ \propto ∝, 这点我们前面也有提及,下面来看看为什么:

从我们上面推出的公式(8)中,我们可以得出:
w = [ ⋮ log P ( t ∣ s ) ⋮ ⋮ log P ( s ∣ s t a r t ) ⋮ log P ( s ′ ∣ s ) ⋮ log P ( e n d ∣ s ) ⋮ ] ϕ ( x , y ) = [ ⋮ N s , t ( x , y ) ⋮ ⋮ N start , s ( x , y ) ⋮ N s , s ′ ( x , y ) ⋮ N s , e n d ( x , y ) ⋮ ] (9) w=\left[\begin{array}{c}{\vdots} \\ {\log P(t | s)} \\ {\vdots} \\ {\vdots} \\ {\log P(s | s t a r t)} \\ {\vdots} \\ {\log P\left(s^{\prime} | s\right)} \\ {\vdots} \\ {\log P(e n d | s)} \\ {\vdots}\end{array}\right] \phi(x, y)=\left[\begin{array}{c}{\vdots} \\ {N_{s, t}(x, y)} \\ {\vdots} \\ \vdots \\ {N_{\text {start}, s}(x, y)} \\ {\vdots} \\ {N_{s, s^{\prime}}(x, y)} \\ {\vdots} \\ {N_{s, e n d}(x, y)} \\ \vdots\end{array}\right] \tag{9} w=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡⋮logP(t∣s)⋮⋮logP(s∣start)⋮logP(s′∣s)⋮logP(end∣s)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ϕ(x,y)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡⋮Ns,t(x,y)⋮⋮Nstart,s(x,y)⋮Ns,s′(x,y)⋮Ns,end(x,y)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(9)
由上面的 w w w向量,我们可以知道每一个权重和几率是有对应关系的,而在 w w w中,权重其实一共分为四种,对应着公式(3),(4),(5),(6)中的每一个子项:
-
词性 s 时为word为 t 的概率:
w s , t = l o g P ( x i = t ∣ y i = s ) → P ( x i = t ∣ y i = s ) = e w s , t w_{s,t} = logP(x_i = t|y_i=s) \rightarrow P(x_i = t|y_i=s) = e^{w_{s,t}} ws,t=logP(xi=t∣yi=s)→P(xi=t∣yi=s)=ews,t -
句首是s概率:
w s t a r t , s = log P ( s ∣ s t a r t ) → P ( s ∣ s t a r t ) = e w s t a r t , s w_{start,s} = \log P(s|start) \rightarrow P(s|start) = e^{w_{start,s}} wstart,s=logP(s∣start)→P(s∣start)=ewstart,s -
词性 s 时后面的词性为 s’ 的概率:
w s , s ′ = l o g P ( y i = s ′ ∣ y i − 1 = s ) → P ( y i = s ′ ∣ y i − 1 = s ) = e w s , s ′ w_{s,s\prime} = logP(y_i = s\prime|y_{i-1}=s) \rightarrow P(y_i = s\prime|y_{i-1}=s) = e^{w_{s,s\prime}} ws,s′=logP(yi=s′∣yi−1=s)→P(yi=s′∣yi−1=s)=ews,s′ -
句尾为s的概率:
w s , e n d = log P ( e n d ∣ s ) → P ( e n d ∣ s ) = e w s , e n d w_{s,end} = \log P(end|s) \rightarrow P(end|s) = e^{w_{s,end}} ws,end=logP(end∣s)→P(end∣s)=ews,end
也就是在 w 里面,每一个weight都对应到HMM里的某个概率取 log,如果想转回概率的话,就把 w 取exp。
而w在训练的过程中,w里面的值是可正可负的,值是负的话,取exp的值是小于1的,可以解释为一个概率,但是如果exp大于1的话,就不能解释为概率了。还有就是given s(tags)后对t(word) summation ,没有办法保证和是1 (因为 P ( x i = t ∣ y i = s ) P(x_i=t|y_i=s) P(xi=t∣yi=s)取了log)。所以没办法说 P ( x , y ) = e x p ( w ⋅ ϕ ( x , y ) ) P(x,y)=exp(w⋅ϕ(x,y)) P(x,y)=exp(w⋅ϕ(x,y))) ,于是就改成正比。
一开始我看见上面的说法的时候,有点疑惑:根据公式(9)中的w,每一项概率P都是小于1的,那么取log后,不是一定小于0吗?为什么会可正可负呢?如果都是小于0,最后 w ⋅ ϕ ( x , y ) w\cdot \phi(x,y) w⋅ϕ(x,y)后再取一个指数e,是一定小于1大于0的,满足概率的呀!?
想了一下,我的理解是:我们在训练的时候,w会随着训练而进行修改,而我们每次训练的时候,可能并不能保证修改后的值是一定小于1的。我们并不能按照概率的思想来想训练的时候w的变化情况!
Feature Vector
下面来看CRF的Feature Vector是什么样子,就是 ϕ ( x , y ) \phi(x,y) ϕ(x,y)这个东西,我们前面已经求出来了:
ϕ ( x , y ) = [ ⋮ N s , t ( x , y ) ⋮ ⋮ N start , s ( x , y ) ⋮ N s , s ′ ( x , y ) ⋮ N s , e n d ( x , y ) ⋮ ] \phi(x, y)=\left[\begin{array}{c}{\vdots} \\ {N_{s, t}(x, y)} \\ {\vdots} \\ \vdots \\ {N_{\text {start}, s}(x, y)} \\ {\vdots} \\ {N_{s, s^{\prime}}(x, y)} \\ {\vdots} \\ {N_{s, e n d}(x, y)} \\ \vdots\end{array}\right] ϕ(x,y)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡⋮Ns,t(x,y)⋮⋮Nstart,s(x,y)⋮Ns,s′(x,y)⋮Ns,end(x,y)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
我们前面也说了, ϕ ( x , y ) \phi(x,y) ϕ(x,y)包含两个大部分:
- 第一个部分是有关tag(词性)和 word(词汇)的关系
- 第二个部分是有关tag(词性)和 tag(词性)之间的关系
又可分为四个小部分;
- 第一个部分是有关tag(词性)和 word(词汇)的关系
- 第三个部分是句子开头的tag(词性),即start 和 tag 的关系
- 第二个部分是句子中tag(词性)和 tag(词性)之间的关系
- 第四个部分是句子结尾的tag(词性),即end 和 tag的关系
下面直接看例子:

先看第一个部分,如上图右边的向量。
定义 N s , t ( x , y ) N_{s,t}(x,y) Ns,t(x,y):为词性s和词汇t在(x, y)对中出现的次数。
定义如果有S个tag,有L个可能的词汇,那向量维度就是 S × L S×L S×L,例如有10种词性,10000个可能的词汇,那向量的长度就是100000维。
向量里面是所有词性跟所有词汇的pair,今天如果给一个(x,y)的pair,“the”标示为D出现2次的话,那向量维度D,the就对应2,没出现的pair都是0。可以想象这个向量的维度非常大,但有值的地方可能很少(稀疏)。

在第二个部分中,是如上图右边的向量。
定义 N S , S ′ ( x , y ) : N_{S, S^{\prime}}(x, y) : NS,S′(x,y):为标记s和s’在(x, y)对中连续出现的次数。
N D , D ( x , y ) N_{D, D}(x, y) ND,D(x,y)表示D后面出现D在(x, y)对中出现的次数,在这个例子中D和D没有接在一起过,所以次数为0;D后面接N出现过2次…
如果有S个可能的标记,其维度为 S × S + 2 S S \times S + 2S S×S+2S(对所有的标记对,我们都需要一个维度,每一个标记跟start产生的对也是一个维度,每一个标记跟end所产生的对又是一个维度,因此所有标记的对为s的平方,start跟end的对为s)。
然后把part1和part2的向量接在一起作为 ϕ ( x , y ) \phi(x,y) ϕ(x,y),这个向量有它自己的含义,跟HMM想要model的东西是一样的。
但是CRF牛叉的地方在于,因为CRF把概率描述成 w w w和 ϕ ( x , y ) \phi(x,y) ϕ(x,y)的inner product,所以这个特征向量可以不这样定义,可以自己来定义 ϕ ( x , y ) \phi(x,y) ϕ(x,y)的形式!
Training Criterion
下面来看CRF如何训练:

假设我们有一组训练数据:
{ ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , ⋯ ( x N , y ^ N ) } \left\{\left(x^{1}, \hat{y}^{1}\right),\left(x^{2}, \hat{y}^{2}\right), \cdots\left(x^{N}, \hat{y}^{N}\right)\right\} {(x1,y^1),(x2,y^2),⋯(xN,y^N)}
找到一个权重向量 W ∗ W^{*} W∗去最大化目标函数 O ( w ) O(w) O(w);
w ∗ = arg max w O ( w ) (1) w^{*}=\arg \max _{w} \mathrm{O}(w) \tag{1} w∗=argwmaxO(w)(1)
其中目标函数 O ( w ) O(w) O(w)为:
O ( w ) = ∑ n = 1 N log P ( y ^ n ∣ x n ) O(w)=\sum_{n=1}^{N} \log P\left(\hat{y}^{n} | x^{n}\right) O(w)=n=1∑NlogP(y^n∣xn)
表示为我们要寻找一个w,使得最大化给定的 x n x_n xn所产生 y ^ n \hat{y}^{n} y^n正确标记的几率,再取对数进行累加。
你会发现和交叉熵很像,交叉熵也是最大化正确维度的几率再取对数,只不过此时是针对整个序列而言的。给定一整个sequence x,我们要让正确的sequence的概率的log越大越好。
根据概率公式:
P ( y ∣ x ) = P ( x , y ) ∑ y ′ P ( x , y ′ ) \begin{array}{l}{P(y | x)} {=\frac{P(x, y)}{\sum_{y^{\prime}} P\left(x, y^{\prime}\right)}}\end{array} P(y∣x)=∑y′P(x,y′)P(x,y)
我们可以很容易对目标函数中的项 l o g P ( y ^ n ∣ x n ) log P(\hat{y}^n|x^n) logP(y^n∣xn)进行转换:
log P ( y ^ n ∣ x n ) = log P ( x n , y ^ n ) − log ∑ y ′ P ( x n , y ′ ) (2) \log P\left(\hat{y}^{n} | x^{n}\right)=\log P\left(x^{n}, \hat{y}^{n}\right)-\log \sum_{y^{\prime}} P\left(x^{n}, y^{\prime}\right) \tag{2} logP(y^n∣xn)=logP(xn,y^n)−logy′∑P(xn,y′)(2)
根据公式(1)知道我们的目标是maximize 目标函数,因此公式(2)真正要做的事情其实就是:
- 最大化 log P ( x n , y ^ n ) \log P\left(x^{n}, \hat{y}^{n}\right) logP(xn,y^n),最大化在训练数据里看到的pair ( x n , y ^ n ) (x^{n}, \hat{y}^{n}) (xn,y^n)的概率
- 最小化 log ∑ y ′ P ( x n , y ′ ) \log \sum_{y^{\prime}} P\left(x^{n}, y^{\prime}\right) log∑y′P(xn,y′),最小化训练数据没有看到的pair的概率
因为是maximize 目标函数,我们又可以知道应该使用Gradient Ascent来更新w的数值:

-
Gradient descent:梯度下降里,最小化代价函数C,计算C的梯度,然后θ减去 η ∇ C ( θ ) η∇C(θ) η∇C(θ)(即往负梯度方向走):
θ → θ − η ∇ C ( θ ) \theta \rightarrow \theta-\eta \nabla C(\theta) θ→θ−η∇C(θ) -
Gradient Ascent:梯度上升了,是θ加上 η ∇ C ( θ ) η∇C(θ) η∇C(θ)(即往梯度方向走):
θ → θ + η ∇ O ( θ ) \theta \rightarrow \theta+\eta \nabla O(\theta) θ→θ+η∇O(θ)
上面只是通用的公式,下面来看看具体怎么弄:

先写出目标函数:
O ( w ) = ∑ n = 1 N log P ( y ^ n ∣ x n ) = ∑ n = 1 N O n ( w ) O(w)=\sum_{n=1}^{N} \log P\left(\hat{y}^{n} | x^{n}\right)=\sum_{n=1}^{N} O^{n}(w) O(w)=n=1∑NlogP(y^n∣xn)=n=1∑NOn(w)
对目标函数中每一项求梯度,可以得到:
∇ O n ( w ) = [ ⋮ ∂ O n ( w ) / ∂ w s , t ⋮ ∂ O n ( w ) / ∂ w s , s ′ ⋮ ] \nabla O^{n}(w)=\left[\begin{array}{c}{\vdots} \\ {\partial O^{n}(w) / \partial w_{s, t}} \\ {\vdots} \\ {\partial O^{n}(w) / \partial w_{s, s^{\prime}}}\\ \vdots\end{array}\right] ∇On(w)=⎣⎢⎢⎢⎢⎢⎢⎢⎡⋮∂On(w)/∂ws,t⋮∂On(w)/∂ws,s′⋮⎦⎥⎥⎥⎥⎥⎥⎥⎤
我们w有很多很多,有的w对应到一个tag和一个word的pair,有的w是对应两个tag的pair。
我们来看看 ∂ O n ( w ) ∂ w s , t \frac{\partial O^n(w)}{\partial w_{s,t}} ∂ws,t∂On(w)如何计算,另外一个 ∂ O n ( w ) ∂ w s , s ′ \frac{\partial O^n(w)}{\partial w_{s,s\prime}} ∂ws,s′∂On(w)是类似的,就不说了!
注意,下面的步骤有点复杂,可以跳过哦~我们后面会直接将偏导后的结果!但其实也并不复杂!

我接下里的过程过程和ppt中的过程有点不大一样,我是根据最终的目标函数来推倒的,但想法是相同的。
有前面可知,我们的目标函数中的每一项其实就是:
O n ( w ) = log P ( y ^ n ∣ x n ) = log P ( x n , y ^ n ) − log ∑ y ′ P ( x n , y ′ ) O^n(w) = \log P\left(\hat{y}^{n} | x^{n}\right)=\log P\left(x^{n}, \hat{y}^{n}\right)-\log \sum_{y^{\prime}} P\left(x^{n}, y^{\prime}\right) On(w)=logP(y^n∣xn)=logP(xn,y^n)−logy′∑P(xn,y′)
由(下面这个式子在我们将CRF开始的时候就已经说过并且证明了):
P ( x , y ) ∝ exp ( w ⋅ ϕ ( x , y ) ) → P ( x , y ) = exp ( w ⋅ ϕ ( x , y ) ) R \mathrm{P}(x, y) \propto \exp (w \cdot \phi(x, y)) \rightarrow P(x,y) = \frac{\exp (w \cdot \phi(x, y))}{R} P(x,y)∝exp(w⋅ϕ(x,y))→P(x,y)=Rexp(w⋅ϕ(x,y))
进一步推导:
O n ( w ) = log exp ( w ⋅ ϕ ( x , y ^ n ) ) R − log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) R = log exp ( w ⋅ ϕ ( x , y ^ n ) ) − log R − log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) + log R = w ⋅ ϕ ( x , y ^ n ) − log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) (1) \begin{aligned} O^n(w) & = \log \frac{\exp (w \cdot \phi(x, \hat{y}^n))}{R} - \log \frac{\sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}{R} \\ &= \log \exp (w \cdot \phi(x, \hat{y}^n)) - \log R - \log \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right) + \log R \\ &= w \cdot \phi(x, \hat{y}^n) - \log \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right) \end{aligned} \tag{1} On(w)=logRexp(w⋅ϕ(x,y^n))−logR∑y′exp(w⋅ϕ(xn,y′))=logexp(w⋅ϕ(x,y^n))−logR−logy′∑exp(w⋅ϕ(xn,y′))+logR=w⋅ϕ(x,y^n)−logy′∑exp(w⋅ϕ(xn,y′))(1)
上式中,最后的结论的第一项其实可以化为:
w ⋅ ϕ ( x , y ^ n ) = ∑ s , t w s , t ⋅ N s , t ( x n , y ^ n ) + ∑ s , s ′ w s , s ′ ⋅ N s , s ′ ( x n , y ^ n ) (2) w \cdot \phi(x,\hat{y}^n) = \sum_{s,t}w_{s,t}\cdot N_{s,t}(x^n,\hat{y}^n)+\sum_{s,s\prime}w_{s,s\prime}\cdot N_{s,s\prime}(x^n,\hat{y}^n) \tag{2} w⋅ϕ(x,y^n)=s,t∑ws,t⋅Ns,t(xn,y^n)+s,s′∑ws,s′⋅Ns,s′(xn,y^n)(2)
其实,也很好理解,因为我们的权值和特征总体上分为两大类,前面有介绍,我们这里就以 w s , t w_{s,t} ws,t来计算,另一个 w s , s ′ w_{s,s\prime} ws,s′也是类似的!
现在来对公式(1)求梯度(偏导):
∂ O n ( w ) ∂ w s , t = ∂ w ⋅ ϕ ( x , y ^ n ) ∂ w s , t + ∂ log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ∂ w s , t (3) \frac{\partial O^n(w)}{\partial w_{s,t}} =\frac{\partial w\cdot\phi(x,\hat{y}^n)}{\partial w_{s,t}}+\frac{\partial \log \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}{\partial w_{s,t}} \tag{3} ∂ws,t∂On(w)=∂ws,t∂w⋅ϕ(x,y^n)+∂ws,t∂log∑y′exp(w⋅ϕ(xn,y′))(3)
因此,根据公式(2),我们公式(3)的第一项就是:
∂ w ⋅ ϕ ( x , y ^ n ) ∂ w s , t = N s , t ( x n , y ^ n ) (4) \frac{\partial w\cdot\phi(x,\hat{y}^n)}{\partial w_{s,t}} = N_{s,t}(x^n,\hat{y}^n) \tag{4} ∂ws,t∂w⋅ϕ(x,y^n)=Ns,t(xn,y^n)(4)

上面我们已经将公式(3)的第一项求导的结果算出来了,就是(4),因此现在我们现在要计算公式(3)的第二项:
∂ log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ∂ w s , t = 1 ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ⋅ ∂ ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ∂ w s , t = 1 ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ⋅ ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ⋅ ϕ ( x n , y ′ ) = ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ) ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ⋅ N s , t ( x n , y ′ ) = ∑ y ′ P ( x n , y ′ ) P ( x n ) ⋅ N s , t ( x n , y ′ ) = ∑ y ′ P ( y ′ ∣ x n ) ⋅ N s , t ( x n , y ′ ) (5) \begin{aligned} \frac{\partial \log \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}{\partial w_{s,t}} &= \frac{1}{\sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}\cdot \frac{\partial \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}{\partial w_{s,t}} \\ &= \frac{1}{\sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}\cdot \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)\cdot \phi(x^n,y\prime) \\ &= \sum_{y\prime} \frac{exp\left(w\cdot\phi(x^n,y\prime)\right))}{\sum_{y\prime} exp\left(w\cdot\phi(x^n,y\prime)\right)} \cdot N_{s,t}(x^n,y\prime) \\ &= \sum_{y\prime} \frac{P(x^n,y\prime)}{P(x^n)} \cdot N_{s,t}(x^n,y\prime) \\ &= \sum_{y\prime}P(y\prime|x^n) \cdot N_{s,t}(x^n,y\prime) \end{aligned} \tag{5} ∂ws,t∂log∑y′exp(w⋅ϕ(xn,y′))=∑y′exp(w⋅ϕ(xn,y′))1⋅∂ws,t∂∑y′exp(w⋅ϕ(xn,y′))=∑y′exp(w⋅ϕ(xn,y′))1⋅y′∑exp(w⋅ϕ(xn,y′))⋅ϕ(xn,y′)=y′∑∑y′exp(w⋅ϕ(xn,y′))exp(w⋅ϕ(xn,y′)))⋅Ns,t(xn,y′)=y′∑P(xn)P(xn,y′)⋅Ns,t(xn,y′)=y′∑P(y′∣xn)⋅Ns,t(xn,y′)(5)
将公式(4)和公式(5)带入公式(3),可以求出梯度为:
∂ O n ( w ) ∂ w s , t = ∂ w ⋅ ϕ ( x , y ^ n ) ∂ w s , t + ∂ log ∑ y ′ e x p ( w ⋅ ϕ ( x n , y ′ ) ) ∂ w s , t = N s , t ( x n , y ^ n ) + ∑ y ′ P ( y ′ ∣ x n ) ⋅ N s , t ( x n , y ′ ) \begin{aligned} \frac{\partial O^n(w)}{\partial w_{s,t}} &=\frac{\partial w\cdot\phi(x,\hat{y}^n)}{\partial w_{s,t}}+\frac{\partial \log \sum_{y\prime}exp\left(w\cdot\phi(x^n,y\prime)\right)}{\partial w_{s,t}} \\ &= N_{s,t}(x^n,\hat{y}^n) + \sum_{y\prime}P(y\prime|x^n) \cdot N_{s,t}(x^n,y\prime) \end{aligned} ∂ws,t∂On(w)=∂ws,t∂w⋅ϕ(x,y^n)+∂ws,t∂log∑y′exp(w⋅ϕ(xn,y′))=Ns,t(xn,y^n)+y′∑P(y′∣xn)⋅Ns,t(xn,y′)
至此证明完毕!
前面没看懂也没事,主要是这个结论:

∂ O n ( w ) ∂ w s , t = N s , t ( x n , y ^ n ) + ∑ y ′ P ( y ′ ∣ x n ) ⋅ N s , t ( x n , y ′ ) \begin{aligned} \frac{\partial O^n(w)}{\partial w_{s,t}} &= N_{s,t}(x^n,\hat{y}^n) + \sum_{y\prime}P(y\prime|x^n) \cdot N_{s,t}(x^n,y\prime) \end{aligned} ∂ws,t∂On(w)=Ns,t(xn,y^n)+y′∑P(y′∣xn)⋅Ns,t(xn,y′)
- 第一项是word t被标识为tag s,在pair ( x n , y ^ n ) (x^n,\hat{y}^n) (xn,y^n)中出现的次数
- 第二项是,summation over所有可能的y ,summation 中每个term是(word t被标识为tag s在 x n x^n xn跟任意一个y的pair中出现的次数)乘上 (给定 x n x^n xn 后任意一个y的概率),y是所有可能出现的sequence,所以非常多。
算出来偏微分的结果,是要跟 w s , t w_{s,t} ws,t 做相加,第一项和第二项是互相对抗的
- 第一项,如果算出来是正的,参数就会增加,算出来是负的,参数就会减少。这个式子告诉我们,如果 s , t s,t s,t 这个pair在正确的训练数据 ( x n , y ^ n ) (x^n,\hat{y}^n) (xn,y^n)中出现的次数越多,那 w s , t w_{s,t} ws,t就会越大。
- 第二项告诉我们,如果 s , t s,t s,t这个pair在任意一个 ( x n , y ) (x^n,y) (xn,y)pair里出现的次数很多的话,那 w s , t w_{s,t} ws,t应该变小
如果 s , t s,t s,t在正确答案里出现的很多,那对应的 w s , t w_{s,t} ws,t就会增加,但是如果不只是在正确答案里出现的次数多,在随便哪个y跟 x n x^n xn pair里出现的次数也多的话,就应该减小 w s , t w_{s,t} ws,t。
今天你要在第二项summation over所有可能的y,可能会卡住,不知道怎么算。但没有关系,这个也可以用维特比算法算。

之前是算了某一个w的偏微分,现在对整个w的偏微分向量就是(正确的 y ^ \hat{y} y^ 形成的特征向量)-(任意y’形成的特征向量∗y’的条件概率):
▽ O ( w ) = ϕ ( x n , y ^ n ) − ∑ y ′ P ( y ′ ∣ x n ) ϕ ( x n , y ′ ) \bigtriangledown O(w) = \phi(x^n,\hat{y}^n)-\sum_{y\prime}P(y\prime|x^n)\phi(x^n,y\prime) ▽O(w)=ϕ(xn,y^n)−y′∑P(y′∣xn)ϕ(xn,y′)
如果我们把随机梯度上升的式子列出来的话
- 每次都取一笔数据 ( x n , y ^ n ) (x^n,\hat{y}^n) (xn,y^n) :
w → w + η ( ϕ ( x n , y ^ n ) − ∑ y ′ P ( y ′ ∣ x n ) ϕ ( x n , y ′ ) ) w \rightarrow w+\eta\left(\phi(x^n,\hat{y}^n)-\sum_{y\prime}P(y\prime|x^n)\phi(x^n,y\prime)\right) w→w+η(ϕ(xn,y^n)−y′∑P(y′∣xn)ϕ(xn,y′))
Inference

把ww向量算出来后,就可以做Q2:推理 了!
我们知道现在要做的事情是,给一个x,找一个y让 P ( y ∣ x ) P(y|x) P(y∣x)最大,在HMM里已经知道,等同于最大化 P ( y ∣ x ) P(y|x) P(y∣x)。在CRF里又知道, P ( y ∣ x ) P(y|x) P(y∣x)是正比于 e x p ( w ⋅ ϕ ( x , y ) ) exp(w⋅ϕ(x,y)) exp(w⋅ϕ(x,y)),代进去等同于是最大化 w ⋅ ϕ ( x , y ) w⋅ϕ(x,y) w⋅ϕ(x,y):
y = arg max y ∈ Y P ( y ∣ x ) = arg max y ∈ Y P ( x , y ) = arg max y ∈ Y w ⋅ ϕ ( x , y ) \begin{aligned} y &=\arg \max _{y \in Y} P(y | x)=\arg \max _{y \in Y} P(x, y) \\ &=\arg \max _{y \in Y} w \cdot \phi(x, y) \end{aligned} y=argy∈YmaxP(y∣x)=argy∈YmaxP(x,y)=argy∈Ymaxw⋅ϕ(x,y)
也可以用维特比算法做。
CRF vs HMM

-
CRF的训练过程中,不只会增加 P ( x , y ^ ) P(x,\hat{y}) P(x,y^) ,还会减少任意一个y和x形成pair的概率;
-
而HMM并没有减少概率这件事情。
我们知道说,如果要得到正确的答案,会希望:
( x , y ^ ) : P ( x , y ^ ) > P ( x , y ) (x, \hat{y}) : P(x, \hat{y})>P(x, y) (x,y^):P(x,y^)>P(x,y)
CRF是增加 P ( x , y ^ ) P(x, \hat{y}) P(x,y^),减小 P ( x , y ) P(x,y) P(x,y),所以CRF更有可能得到正确的结果。
举例来说,用之前HMM的例子:
-
根据训练数据,HMM给了如上图左下方所示的结果(直接统计来的),HMM说 y i y_i yi应该是V:
P ( V ∣ N ) ⋅ P ( a ∣ V ) = 0.45 > P ( D ∣ N ) ⋅ P ( a ∣ D ) = 0.1 P(V|N)\cdot P(a|V) = 0.45 \gt P(D|N)\cdot P(a|D) = 0.1 P(V∣N)⋅P(a∣V)=0.45>P(D∣N)⋅P(a∣D)=0.1
但你会发现这种情况在我们的训练数据(上图左下角)中并没有出现过! -
但是CRF不关心概率,就是调整w参数使得正确的(x,y) pair的分数比较大。所以CRF可能调来调去,使得P(a|V)到0.1,使得 y i y_i yi可能是D:
P ( D ∣ N ) ⋅ P ( a ∣ D ) = 0.1 > P ( V ∣ N ) ⋅ P ( a ∣ V ) = 0.09 P(D|N)\cdot P(a|D)=0.1 \gt P(V|N)\cdot P(a|V) = 0.09 P(D∣N)⋅P(a∣D)=0.1>P(V∣N)⋅P(a∣V)=0.09
Synthetic Data(合成数据)

以下是一个综合的实验,比较CRF和HMM有什么不一样。
在这个实验里面,input是小写的a到z ,output是大写的A到E:
x i ∈ { a − z } , y i ∈ { A − E } x_{i} \in\{a-z\}, y_{i} \in\{A-E\} xi∈{a−z},yi∈{A−E}
然后我们要生成一些人工数据,这些数据使用HMM生成的,但用的不是一般的HMM,用的是一个mixed-order HMM(混合顺序隐马尔科夫模型)。
-
转移概率是:
α P ( y i ∣ y i − 1 ) + ( 1 − α ) P ( y i ∣ y i − 1 , y i − 2 ) \alpha P\left(y_{i} | y_{i-1}\right)+(1-\alpha) P\left(y_{i} | y_{i-1}, y_{i-2}\right) αP(yi∣yi−1)+(1−α)P(yi∣yi−1,yi−2)
如果 α = 1 \alpha=1 α=1,则后面一项是0,就是一般的HMM的转移概率。今天 α \alpha α 的值可以任意调整,考虑一个order的比率大,还是两个order的比率大。 -
发射概率是:
α P ( x i ∣ y i ) + ( 1 − α ) P ( x i ∣ y i , x i − 1 ) \alpha P\left(x_{i} | y_{i}\right)+(1-\alpha) P\left(x_{i} | y_{i}, x_{i-1}\right) αP(xi∣yi)+(1−α)P(xi∣yi,xi−1)
如果 α = 1 \alpha=1 α=1,也就是一般的HMM。
比较HMM和CRF(都是一般的HMM和CRF),HMM只考虑一个order( α = 1 \alpha=1 α=1的状况) 。
一般而言,如果 α \alpha α 越小,那么跟一般的HMM和CRF差距越大,得到的performance越差。但是我们想要知道在这种情况下,到底是HMM坏得比较厉害,还是CRF坏得比较厉害。

上图是实验的结果,每个圈圈是不同的 α \alpha α 得到的结果。从左下到右上代表 α \alpha α 由大到小,每个点都做HMM和CRF的实验,横轴和纵轴代表HMM和CRF犯错的百分比。
可以想象如果一个点在45度角的右侧,代表说HMM犯得错多,CRF犯得错少。从实验结果可以发现,非实心的点是 α > 1 2 \alpha \gt \frac{1}{2} α>21,接近一般的HMM或者CRF,在这个状况下HMM是比CRF好的,也不用意外,因为数据是从HMM产生的,所以HMM的假设更贴近数据的产生方式。 α < 1 2 \alpha \lt \frac{1}{2} α<21时,也就是数据的产生方式和HMM、CRF的假设都不合时,这时候CRF就会比HMM好。因此此时HMM只能按照概率,而CRF会调整参数去fit数据,就算有些假设没有被model在CRF里面,也可以借由调整参数考虑到这些假设,所以当你的模型和数据背后的假设不合时,CRF的表现就会比较好。
Summary

上图是CRF的总结。CRF也是一个结构化学习的方法,解决了3个问题。
-
Q1:评估
F(x,y)是P(y|x):
F ( x , y ) = P ( y ∣ x ) = exp ( w ⋅ ϕ ( x , y ) ) ∑ y ′ ∈ Y exp ( w ⋅ ϕ ( x , y ′ ) ) F(x, y)=P(y | x)=\frac{\exp (w \cdot \phi(x, y))}{\sum_{y^{\prime} \in \mathbb{Y}} \exp \left(w \cdot \phi\left(x, y^{\prime}\right)\right)} F(x,y)=P(y∣x)=∑y′∈Yexp(w⋅ϕ(x,y′))exp(w⋅ϕ(x,y)) -
Q2:推理
找使 w ⋅ ϕ ( x , y ) w⋅ϕ(x,y) w⋅ϕ(x,y)最大的 y ~ \tilde{y} y~ ,利用维特比算法求解:
y ~ = arg max y ∈ Y P ( y ∣ x ) = arg max y ∈ Y w ⋅ ϕ ( x , y ) \tilde{y}=\arg \max _{y \in \mathbb{Y}} P(y | x)=\arg \max _{y \in \mathbb{Y}} w \cdot \phi(x, y) y~=argy∈YmaxP(y∣x)=argy∈Ymaxw⋅ϕ(x,y) -
Q3:训练
一般文献是写成相乘:
w ∗ = arg max w ∏ n = 1 P ( y ^ n ∣ x n ) {w^{*}=\arg \max _{w} \prod_{n=1} P\left(\hat{y}^{n} | x^{n}\right)} w∗=argwmaxn=1∏P(y^n∣xn)但是也可以取log,变成相加(这中形式也是我们前面所讲的):
w ∗ = arg max w ∑ n = 1 N log P ( y ^ n ∣ x n ) w^* = \arg \max\limits_w \sum_{n=1}^{N} \log P\left(\hat{y}^{n} | x^{n}\right) w∗=argwmaxn=1∑NlogP(y^n∣xn)
使用梯度上升求解w:
w → w + η ( ϕ ( x n , y ^ n ) − ∑ y ′ P ( y ′ ∣ x n ) ϕ ( x n , y ′ ) ) {\mathbf{w} \rightarrow w+\eta\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\sum_{y^{\prime}} P\left(y^{\prime} | x^{n}\right) \phi\left(x^{n}, y^{\prime}\right)\right)} w→w+η⎝⎛ϕ(xn,y^n)−y′∑P(y′∣xn)ϕ(xn,y′)⎠⎞
Structured Perceptron/SVM
Structured Perceptron
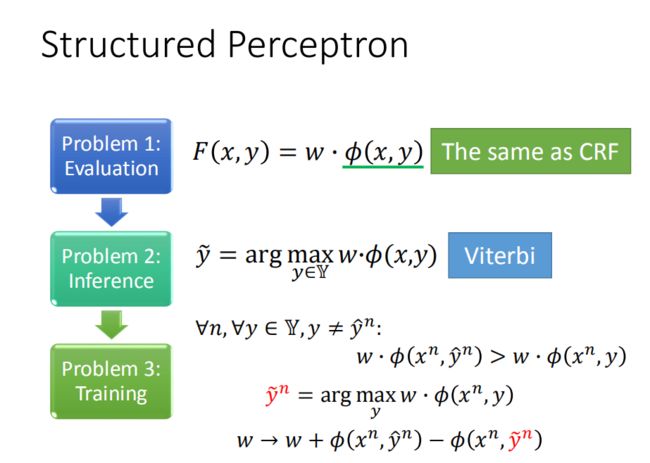
也是那三个问题吧,我们前面已经讲烂了~:
-
Q1:评估
F ( x , y ) = w ⋅ ϕ ( x , y ) F(x,y) = w\cdot \phi(x,y) F(x,y)=w⋅ϕ(x,y)
你可以会说,如果x,y都是sequence的话,这个ϕ()应该定成什么样子?可以选择自己喜欢的方式,最简单的方式就是拿CRF的形式做就好了。 -
Q2:推理
y ~ = arg max y ∈ Y w ⋅ ϕ ( x , y ) \tilde{y} = \arg \max_{y\in Y}w\cdot \phi(x,y) y~=argy∈Ymaxw⋅ϕ(x,y)
一样使用维特比算法求解。 -
Q3:训练
对所有的训练数据n,和所有不等于 y ^ \hat{y} y^的y,我们希望让 w ⋅ ϕ ( x n , y ^ n ) w\cdot \phi(x^n,\hat{y}^n) w⋅ϕ(xn,y^n)大于 w ⋅ ϕ ( x n , y ) w\cdot \phi(x^n,y) w⋅ϕ(xn,y):
∀ n , ∀ y ∈ Y , y ≠ y ^ n : w ⋅ ϕ ( x n , y ^ n ) > w ⋅ ϕ ( x n , y ) \forall n,\forall y \in Y,y\ne\hat{y}^n :\ \ \ \ \ \ w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)>w \cdot \phi\left(x^{n}, y\right) ∀n,∀y∈Y,y=y^n: w⋅ϕ(xn,y^n)>w⋅ϕ(xn,y)
这件事在结构化感知机里,我们会找一个 y ~ \tilde{y} y~(根据目前的w,让式子最大):
y ~ n = arg max y w ⋅ ϕ ( x n , y ) \tilde{y}^{n}=\arg \max _{y} w \cdot \phi\left(x^{n}, y\right) y~n=argymaxw⋅ϕ(xn,y)
接下来更新w:
w → w + ϕ ( x n , y ^ n ) − ϕ ( x n , y ~ n ) w \rightarrow w+\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \tilde{y}^{n}\right) w→w+ϕ(xn,y^n)−ϕ(xn,y~n)
Structured Perceptron vs CRF

你有没有觉得结构化感知机w更新很眼熟呢,和CRF的梯度上升很像?
在CRF梯度上升里,如果忽略掉 η \eta η (学习率),那跟结构化感知机一样都有两项(绿色线项和紫色线项)。绿色项是一样的,紫色项虽然看起来不一样,但其实是很有关系的:
-
Structured Perceptron里则是某一个 y ~ \tilde{y} y~ 的特征向量,而 y ~ \tilde{y} y~ 可以让 w ⋅ ϕ ( x n , y ) w⋅ϕ(x^n,y) w⋅ϕ(xn,y)最大, y ~ \tilde{y} y~ 其实就是让概率 P ( y ∣ x n ) P(y|x^n) P(y∣xn)最大y:
y ~ n = arg max y w ⋅ ϕ ( x n , y ) ϕ ( x n , y ~ n ) \begin{array}{l}{\tilde{y}^{n}=\arg \max _{y} w \cdot \phi\left(x^{n}, y\right)} \\ \phi(x^n,\tilde{y}^n)\end{array} y~n=argmaxyw⋅ϕ(xn,y)ϕ(xn,y~n)
这一项也叫做Hard(硬范畴)! -
CRF里是summation over所有的y的特征向量,再做weight sum:
∑ y ′ P ( y ′ ∣ x n ) ϕ ( x n , y ′ ) \sum_{y^{\prime}} P\left(y^{\prime} | x^{n}\right) \phi\left(x^{n}, y^{\prime}\right) y′∑P(y′∣xn)ϕ(xn,y′)
这一项也叫做Soft(软范畴)!
所以Structured Perceptron是减去Hard(硬范畴):
y ~ n = arg max y w ⋅ ϕ ( x n , y ) w → w + ϕ ( x n , y ^ n ) − ϕ ( x n , y ~ n ) \begin{array}{l}{\tilde{y}^{n}=\arg \max _{y} w \cdot \phi\left(x^{n}, y\right)} \\ {w \rightarrow w+\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \tilde{y}^{n}\right)}\end{array} y~n=argmaxyw⋅ϕ(xn,y)w→w+ϕ(xn,y^n)−ϕ(xn,y~n)
而CRF是Soft(软范畴):
w → w + η ( ϕ ( x n , y ^ n ) ‾ − ∑ y ′ P ( y ′ ∣ x n ) ϕ ( x n , y ′ ) ) \mathrm{w} \rightarrow w+\eta\left(\underline{\phi\left(x^{n}, \hat{y}^{n}\right)}-\sum_{y^{\prime}} P\left(y^{\prime} | x^{n}\right) \phi\left(x^{n}, y^{\prime}\right)\right) w→w+η⎝⎛ϕ(xn,y^n)−y′<