强化学习原理python篇05——蒙特卡罗方法

本章全篇参考赵世钰老师的教材 Mathmatical-Foundation-of-Reinforcement-Learning Monte Carlo Methods章节，请各位结合阅读，本合集只专注于数学概念的代码实现。

蒙特卡罗方法

蒙特卡罗方法是一种基于随机模拟的数值计算方法，它的名字来源于摩纳哥的蒙特卡罗赌场。蒙特卡罗方法通过使用随机数来解决复杂的数学问题，它主要用于求解无法通过解析方法或确定性算法求解的问题。

仍以上节课做例子

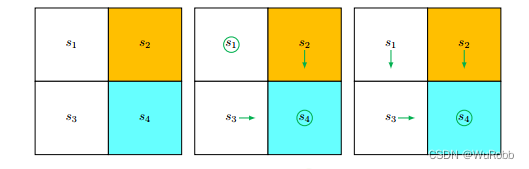
写一个模拟该实验的类，用坐标（0，1）代表s1，（1，1）代表s2，（0，0）代表s3，（1，0）代表s4

import gym
import numpy as np
import pygame
from gym import spaces

class MyEnv(gym.Env):
    # 继承父类
    def __init__(self, n_grid, R, init_state, max_steps):
        # 设置观察空间
        self.observation_space = spaces.Dict(
            {
                # Box（上界，下界， 形状，这里建立一个二维网格世界）
                "agent": spaces.Box(0, n_grid - 1, shape=(2,), dtype=int),
                "target": spaces.Box(0, n_grid - 1, shape=(2,), dtype=int),
            }
        )

        # 上界
        self.upper_bounds = n_grid - 1

        # 设置行动空间
        # 向上，向右，向下，向左，不动
        self.action_space = spaces.Discrete(5)

        # 初始状态
        self.init_state = init_state
        self.cur_state = init_state

        # 游戏次数
        self.init_step = 0
        self.max_steps = max_steps

        self.R = np.flip(R, axis=0).T

    # agent 开始行动
    def step(self, action):
        # 控制行动次数
        self.init_step += 1
        terminated = False
        if self.init_step >= self.max_steps:
            terminated = True

        reward = None
        cur_state = self.cur_state
        # 向上
        if action == 0:
            if cur_state[1] + 1 <= self.upper_bounds:
                cur_state[1] = cur_state[1] + 1
            else:
                cur_state[1] = self.upper_bounds
                reward = -1

        # 向右
        elif action == 1:
            if cur_state[0] + 1 <= self.upper_bounds:
                cur_state[0] = cur_state[0] + 1
            else:
                cur_state[0] = self.upper_bounds
                reward = -1

        # 向下
        elif action == 2:
            if cur_state[1] - 1 >= 0:
                cur_state[1] = cur_state[1] - 1
            else:
                cur_state[1] = 0
                reward = -1
        # 向左
        elif action == 3:
            if cur_state[0] - 1 >= 0:
                cur_state[0] = cur_state[0] - 1
            else:
                cur_state[0] = 0
                reward = -1
        # 不动
        elif action == 4:
            cur_state = cur_state

        # 更新状态
        if not reward:
            reward = self.R[cur_state[0], cur_state[1]]
        info = {
            "action_name": {0: "向上", 1: "向右", 2: "向下", 3: "向左", 4: "不动"},
            "state_name": {
                str([0, 1]): "s1",
                str([1, 1]): "s2",
                str([0, 0]): "s3",
                str([1, 0]): "s4",
            },
        }

        return cur_state, reward, terminated, False, info

    def reset(self):
        self.cur_state = self.init_state.copy()
        self.init_step = 0
        return self.cur_state.copy(), {}

    def discount_reward(self, R, gamma):
        # r 为历史得分
        n = len(R)
        dr = 0
        for i in range(n):
            dr += gamma**i * R[i]
        return dr

测试一下

R = np.array([[0, -1], [0, 1]])

env = MyEnv(n_grid=R.shape[0], R=R, init_state=[0, 1], max_steps=100)
action_space = env.action_space

obj, info = env.reset()
idx = 0
R_history = []
total_R = 0
gamma = 0.8
while True:
    idx += 1
    action = action_space.sample()
    new_obj, reward, terminated, truncated, info = env.step(action)

    total_R += reward
    R_history.append(reward)
    print(
        info["state_name"][str(obj)],
        "--",
        info["action_name"][action],
        "-->",
        info["state_name"][str(new_obj)],
        reward,
    )
    obj = new_obj.copy()
    if terminated:
        break
print(total_R)
print("discount_reward: ", env.discount_reward(R_history, gamma))

输出：

s1 -- 向右 --> s2 -1
s2 -- 向左 --> s1 0
s1 -- 向上 --> s1 -1
s1 -- 向左 --> s1 -1
s1 -- 向上 --> s1 -1
s1 -- 向右 --> s2 -1
s2 -- 向下 --> s4 1
s4 -- 向右 --> s4 -1
s4 -- 向下 --> s4 -1
s4 -- 向下 --> s4 -1
s4 -- 向下 --> s4 -1
s4 -- 向右 --> s4 -1
s4 -- 不动 --> s4 1

则对于左上角的状态s1，重复模拟实验，获得1000次discount reward

通过随机采样的方法对问题进行近似求解,对action value进行均值估计。

def discount_reward(R, gamma):
    # R 为历史得分
    n = len(R)
    dr = 0
    for i in range(n):
        dr += gamma**i * R[i]
    return dr


def action_value(max_steps, s_action, gamma, R):
    env = MyEnv(n_grid=R.shape[0], R=R, init_state=[0, 1], max_steps=max_steps)
    action_space = env.action_space
    obj, info = env.reset()

    R_history = []

    # 指定s_action 运行
    new_obj, reward, terminated, truncated, info = env.step(s_action)
    R_history.append(reward)

    # 后自己运作
    while True:
        action = action_space.sample()
        new_obj, reward, terminated, truncated, info = env.step(action)

        R_history.append(reward)
        # print(
        #     obj, '--->', new_obj, reward, info['action_name'][action]
        # )
        # obj = new_obj.copy()
        if terminated:
            break
    return discount_reward(R_history, gamma)

history_action_value = {
    0: [],
    1: [],
    2: [],
    3: [],
    4: [],
}

# 重复一百次实验
for iter in range(100):
    for i in range(5):
        eval_action_value = action_value(1000, i, 0.8, R)
        history_action_value[i].append(eval_action_value)

# 均值估计action_value
for i in history_action_value.keys():
    history_action_value[i] = np.mean(history_action_value[i])
history_action_value
    

输出：

{0: -2.7169440173670263,
 1: -2.6544426689552973,
 2: -1.3196635942355959,
 3: -3.0233051053797015,
 4: -1.9523732005742196}

则最大的action_value对应的action为2，则选择向下走。

Ref

Mathematical Foundations of Reinforcement Learning，Shiyu Zhao