图像处理常用算法介绍
此篇简单回顾下图像处理领域常用到的一些算法，这边只对每个知识点重要的点做一些记录，便于快速的知其形，会其意。
一. SIFT（Scale-Invariant feature transform)特征
重点是了解DOG(Difference of Gaussian)高斯差分图像是如何生成的，以及求取关键点，求取关键点的主方向，并以此主方向来做坐标系，梯度方向和梯度幅值按新的坐标系进行计算，构造一个特征向量描述子。主要可参考如下博客
SIFT局部描述子 - 知乎
https://www.cnblogs.com/Jack-Elvis/p/11297216.html
SIFT算法原理与源码分析
二. PCA
可参考博主的论文
这边投影的一些知识点拓展也可以参考之前的博客中第17点
线性代数基础知识-CSDN博客
这里其实就是通过PCA去求新的坐标系的各坐标轴，一个轴可以认为就是一个特征向量。d个特征向量即为d个轴。然后k等同于选取了其中的k个轴，只获取原数据在这k个轴上的投影值组成一个特征向量来表示图像。
也可以参考其它博客
PCA(主成分分析) - 知乎
【机器学习】降维——PCA（非常详细） - 知乎
三. SVD
上面最后一个参考博客中也提到了SVD，其左奇异矩阵和右奇异矩阵介绍可见如下帖子
降维算法: 奇异值分解SVD - 知乎
《统计学习方法》之SVD - 知乎
具体计算示例可参考如下博客
强大的矩阵奇异值分解(SVD) - 知乎
回想之前在校期间，用PCA对图像提取特征时，需要计算
, 当是一张2000*2000大小图片时，由于直接将图像拉伸为向量，一个样本将达到400万长的一个维度。假设这边有1000个样本，A的大小将会是100万* 1000, 所以将会100万* 100万大小，Matbalb计算时候直接显示内存不足，当时就转用SVD方法去求解。 我们可以用SVD方法，将A表达为:
，那么协方差矩阵
= 
* 
= 
，转换为了U的计算
【数学和算法】SVD奇异值分解原理、以及在PCA中的运用_svd怎么在pca-CSDN博客
PCA和SVD的联系和区别？ - 知乎
如下博客很好的说明了SVD在图像压缩上的一个应用
SVD与图像压缩 - 知乎
四. 矩阵的迹
关于矩阵迹的相关性质 - 知乎
高等代数|第四章 矩阵--矩阵的迹与相似
五. 牛顿法
涉及到泰勒展开（其实就是在一个点附近，用多项式去无限逼近此函数），下面先回顾下一些基本知识点
泰勒展开百度安全验证
讲透泰勒公式，让你成为高手！ - 知乎
[计算机数值分析]牛顿法求解方程的根-CSDN博客
最优化方法复习笔记（三）牛顿法及其收敛性分析 - 知乎
牛顿迭代法（求函数的根）_迭代法函数必须单调-CSDN博客
牛顿法的优缺点及特征_newton迭代法的优缺点-CSDN博客
六. 梯度下降算法
为什么局部下降最快的方向就是梯度的负方向？ - 知乎
最优化方法之梯度下降法和牛顿法_优化问题目标函数的梯度怎么求-CSDN博客
七. EM算法
EM算法详解 - 知乎
【大道至简】机器学习算法之EM算法(Expectation Maximization Algorithm)详解(附代码)---通俗理解EM算法。-CSDN博客
八. 几个矩阵的含义
雅可比（Jacobian）矩阵_雅可比矩阵-CSDN博客
Jacobian矩阵和Hessian矩阵 - 知乎
雅克比矩阵的意义 - 知乎
雅可比矩阵几何意义的直观解释及应用-CSDN博客
九. 最小二乘法
最小二乘法 (Least Squares) - 知乎
GD&T干货 | 最小二乘法的数学公式详解 - 知乎
十. RANSAC算法
RANSAC算法_51CTO博客_kmeans聚类算法
RANSAC算法（仅供学习使用）-CSDN博客
https://www.cnblogs.com/xrwang/archive/2011/03/09/ransac-1.html
RANSAC算法 - 知乎
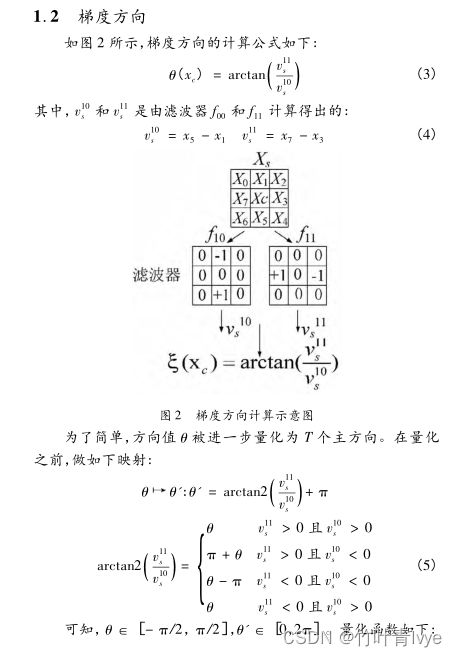
十一. 梯度方向直方图
一文讲解方向梯度直方图（hog） - 知乎
博主之前相关的论文
后面有时间会再继续概括！