区字棋中的最长非0链

目录

一，区字棋

二，不败策略

三，有向有环图分析

1，最长非零链

2，详细有向有环图

---

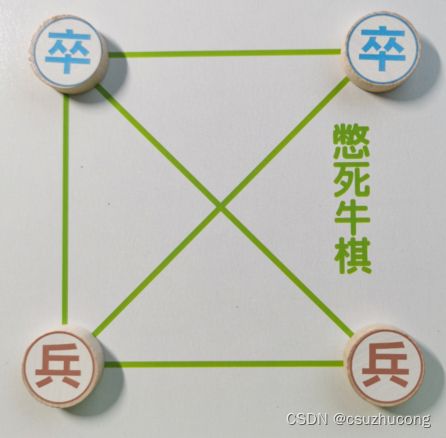
一，区字棋

也叫憋死牛棋。

规则：

棋盘一共只有5个点，双方各2个棋子，还有一个空格。

先手必须移动左边的棋子，之后没有限制，2个棋子任意一个移动到空格皆可。

无法移动者判负。

二，不败策略

因为失败的阵型是固定的，要么2个都在上面，要么2个都在下面，只有这样才有可能被堵住。

所以不败策略也很简单，任意状态下，轮到任意方行动时，都至少有1种行动方法，不会走到固定的失败阵型，这就是不败策略了。

三，有向有环图分析

1，最长非零链

用博弈论分析，这个属于有向有环图游戏，上面的不败策略其实就是说，该有向图的等价图中，最长的非零链的长度为2，即1个回合。

我们来验证一下。

（1）给所有状态编号

假设轮到某一方行动时，他的2个棋子分别在i,j，空格在k，那么我们编号为i*25+j*5+k，其中0<=i,j,k<=5

所有状态的编号都在0到124之间，但其中有小部分是非法状态（ijk重复），合法状态只有60种。

考虑到2个棋子相同的话，实际上只有30个不同的合法状态。

（2）构建有向图

int getId(int i, int j, int k) {
    return i * 25 + j * 5 + k;
}
int getId(vectorv) {
    int i = v[0], j = v[1], k = v[2];
    return i * 25 + j * 5 + k;
}
vector getIjk(int id) {
    return vector{id / 25, id % 25 / 5, id % 5};
}
bool isConnect(int x, int y) {
    if (x == 2 || y == 2)return true;
    if (x > y)x ^= y ^= x ^= y;
    if (x == 0)return y < 4;
    return x==3;
}
vectorreverseTurn(int i, int j, int k) {
    int ni = 0, nj = 0;
    while (ni == i || ni == j || ni == k)ni++;
    while (nj == i || nj == j || nj == k||nj==ni)nj++;
    return vector{ni, nj, k};
}
vector getNext(int id) {
    auto v = getIjk(id);
    int i = v[0], j = v[1], k = v[2];
    vectorans;
    if (isConnect(k, i))ans.push_back(getId(reverseTurn(k, j, i)));
    if (isConnect(k, j))ans.push_back(getId(reverseTurn(i, k, j)));
    return ans;
}
map> bfs(int id)
{
    queueq;
    q.push(id);
    mapvisit;
    visit[id] = 1;
    map>ans;
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        auto v = getNext(t);
        ans[t] = v;
        for (auto x : v) {
            if (visit[x])continue;
            visit[x] = 1;
            q.push(x);
        }
    }
    return ans;
}

（3）调用有向有环图游戏的模板，统计最长非0链

int main()
{
    int id = getId(3, 4, 0);
    map> g = bfs(id);
    map out;
    map>rg;
    maps;
    for (auto gi : g) {
        out[gi.first] = gi.second.size();
        if (out[gi.first] == 0)s[gi.first] = -1;
        for (auto x : gi.second) {
            rg[x].push_back(gi.first);
        }
    }
    JudgeDirectedCyclicGraph::solve(out, rg, s);
    return 0;
}

输出：

fromV1ToV2
fromV2ToV1

所以，最长非零链长度为2

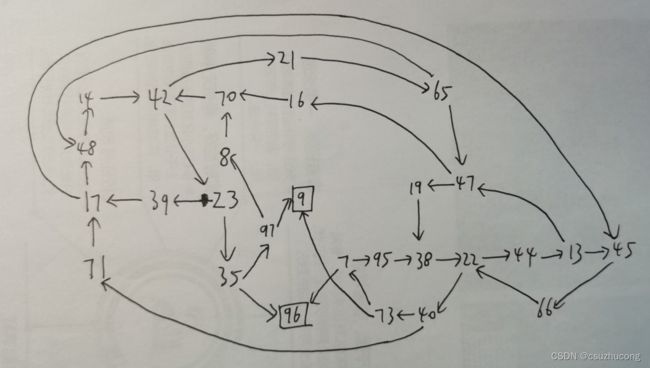
2，详细有向有环图

其中，9和96是负节点，7,35,73,97是胜节点，其他22个节点都是平节点。

本来应该有30个节点，但是有2个节点是不可达的，分别是（0,2,1）和（2,3,4）