Day22|leetcode235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点

leetcode 235. 二叉搜索树的最近公共祖先

题目链接：235. 二叉搜索树的最近公共祖先 - 力扣（LeetCode）

视频链接：二叉搜索树找祖先就有点不一样了！| 235. 二叉搜索树的最近公共祖先_哔哩哔哩_bilibili

题目概述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

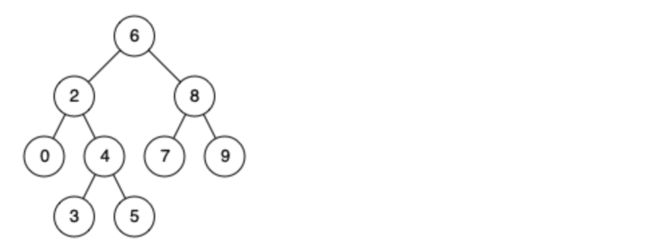
例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

• 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
• 输出: 6
• 解释: 节点 2 和节点 8 的最近公共祖先是 6。

思路

这道题既然是二叉搜索树，就该想到二叉搜索树的有序性，那么，它的有序性就免不了被我们利用一番了，本题用哪种遍历顺序都无所谓，因为中可有可无，把左和右整好就行了。

因为二叉搜索树是有序的，所以如果当我们从上往下遍历时，在根节点的时候，如果它的值比p和q大，那么p和q的公共祖先一定在节点的左子树，所以根据二叉搜索树的特性来往下遍历就行。还要考虑的一点就是节点一定是最近的公共祖先吗？就拿下图举例，当我们遍历到根节点时，根节点为10，比p、q都大，所以p、q的公共祖先在左子树，于是开始往下（左子树）遍历，到5的时候，5是处于p、q值之间的，所以说p、q就分别是5的左右子树，接下来不论5是向左遍历，还是向右遍历，它都会错过p或者q其中之一，由此证明第一次遇到节点的数值在p、q区间中，那么这个节点就是 p和q的最近公共祖先。

代码实现

class Solution {
private:
    TreeNode* traversal(TreeNode* cur,TreeNode* p,TreeNode* q) {
        if(cur == NULL) return cur;
        if(cur->val > p->val && cur->val > q->val) {
            TreeNode* left = traversal(cur->left,p,q);
            if(left != NULL) {
                return left;
            }
        }
        if(cur->val < p->val && cur->val < q->val) {
            TreeNode* right = traversal(cur->right,p,q);
            if(right != NULL) {
            return right;
        }
    }
    return cur;
}   
public:
        TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
            return traversal(root,p,q);
        
    }
};

leetcode 701.二叉搜索树中的插入操作

题目链接：701. 二叉搜索树中的插入操作 - 力扣（LeetCode）

视频链接：原来这么简单？ | LeetCode：701.二叉搜索树中的插入操作_哔哩哔哩_bilibili

题目概述

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

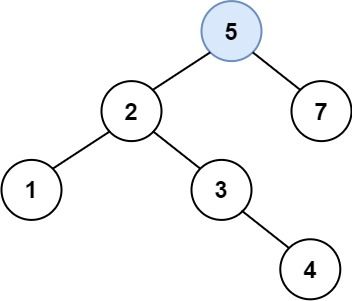
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

思路

其实这道题不用想得那么复杂，不要说给你一个数，你就想着要把二叉搜索树给拆了，把这个数加进去，这样反倒复杂了，其实你只需要把让插入的数加到二叉搜索树的叶子节点上就好了，想明白这点，这道题还挺简单的。

代码实现

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if (root->val > val) root->left = insertIntoBST(root->left, val);
        if (root->val < val) root->right = insertIntoBST(root->right, val);
        return root;
    }
};

leetcode 450.删除二叉搜索树中的节点

题目链接：450. 删除二叉搜索树中的节点 - 力扣（LeetCode）

视频链接：调整二叉树的结构最难！| LeetCode：450.删除二叉搜索树中的节点_哔哩哔哩_bilibili

题目概述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

思路

这道题可比上一道（701）题难多了，因为这道题需要改树的结构，要考虑的情况也很多。

第一种情况：树里没有找到要删除的点。

（下面四种情况为树里有需要删除的点）

第二种情况：要删除的点是最后一个点（也就是叶子节点），这种情况简单，直接删了就行。

第三种情况：左不空，有空。可以这样去想，你们一家三口用一根绳子去拖车，你的长辈在最前面打头拉车，你在你长辈后面拉车，你后面是你小辈拉车，当你受伤下去的时候，你后面的小辈就会代替你的位置，排到你长辈后面去拉车。

第四种情况：左空，右不空。（可以按照情况三举的例子去想）

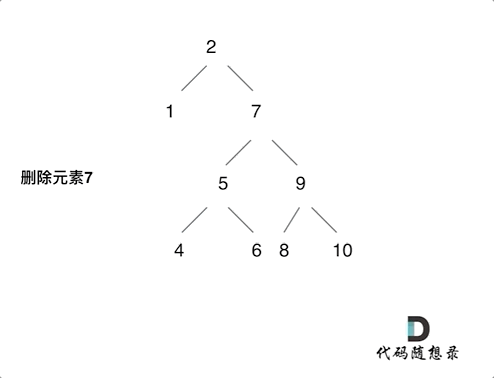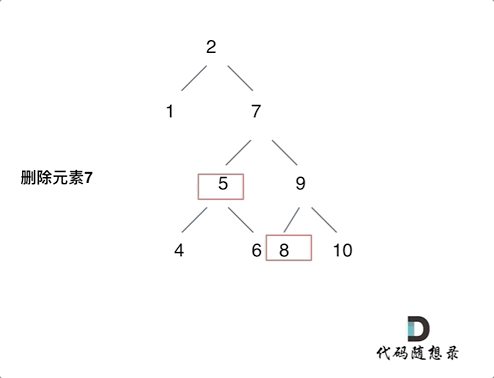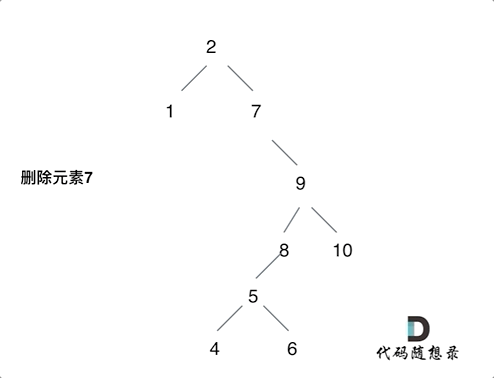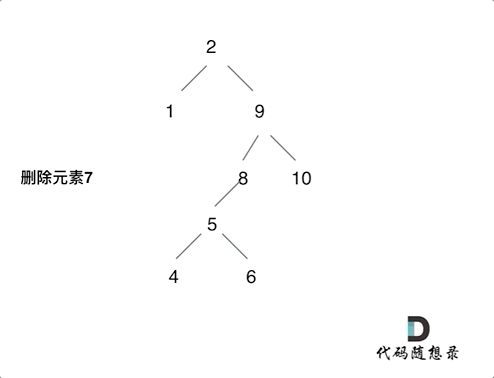
第五种情况：左右都不为空。将删除点的左子树接到右子树最左边的孩子上，如图所示：

这些情况可以自己去画一画，感受一下。 

代码实现

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
        if (root->val == key) {
            // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
            if (root->left == nullptr && root->right == nullptr) {
                ///! 内存释放
                delete root;
                return nullptr;
            }
            // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
            else if (root->left == nullptr) {
                auto retNode = root->right;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if (root->right == nullptr) {
                auto retNode = root->left;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
            // 并返回删除节点右孩子为新的根节点。
            else {
                TreeNode* cur = root->right; // 找右子树最左面的节点
                while(cur->left != nullptr) {
                    cur = cur->left;
                }
                cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
                TreeNode* tmp = root;   // 把root节点保存一下，下面来删除
                root = root->right;     // 返回旧root的右孩子作为新root
                delete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）
                return root;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

写完代码记得要手动释放内存。