【数据结构】详细解读 Splay Tree（附完整代码）

详细解读 Splay Tree（伸展树）

昨天在研究决策树时遇到了一种特殊的搜索平衡二叉树Splay，很感兴趣，今天下午就深入了解了一下这种树。
前部分代码参考了书，后部分为原创，可能有误，敬请批评指正！

Splay树的介绍

Splay树为BST（Binary Search Tree二叉搜索树）的一种，只要是Treap、AVL、红黑树能做的，Splay树都能做。其插入、查找、删除等等操作都是 $O(lo{g}_{2}n)$。
Splay树与其他BST不同的是，它具有把某个结点向上旋转至某位置的能力，包括旋转至根节点（这种方式我们称之为Splay）。
在查询系统中，如果经常查询某个结点，就可以通过Splay操作给它转到根结点上，这样一来下一次查这个结点就省事多了。

旋转（Rotate）

Splay树能在保持伸展树有序的情况下，把x移动到root（根节点）的位置。而这一操作依靠旋转（Rotate）进行，对应函数为Splay(x, root)。
针对不同位置的x，Splay树有不同的旋转方式。

旋转方式

名词介绍：

ZIG：右旋
ZAG：左旋

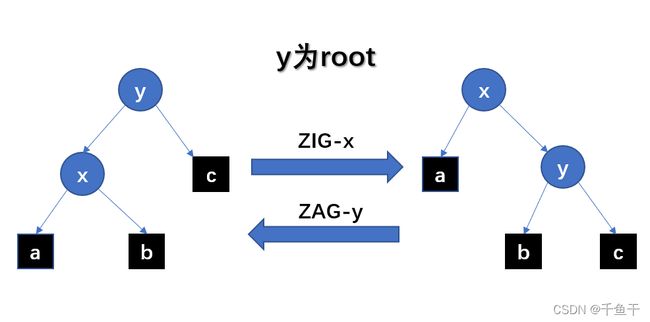
第一种：ZIG / ZAG

若结点x的父结点y是根节点。此时只需要将x右旋即可。同样的，若结点y的父结点x是根节点。此时只需要将y左旋即可。
以左图->右图的操作为例：
1.将x的右子树挂在y的左子树上;
2.将x右旋，时x变为根节点。

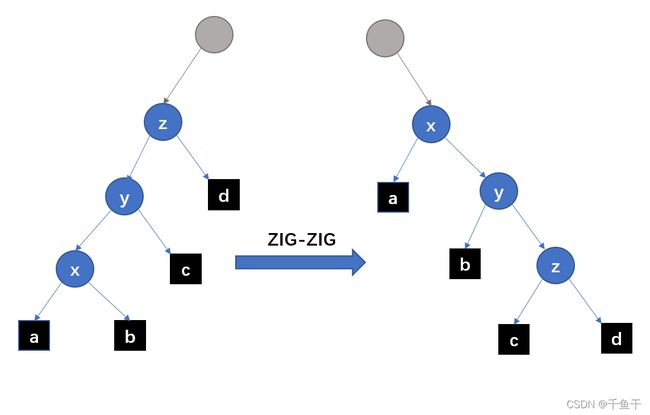
第二种：ZIG-ZIG / ZAG-ZAG

x的父结点y不是根节点，y的父结点为z，且x与y同时是各自父结点的左孩子或者同时是各自父结点的右孩子。此时进行一次ZIG-ZIG或ZAG-ZAG操作。
注意：此时z结点不一定是根结点。

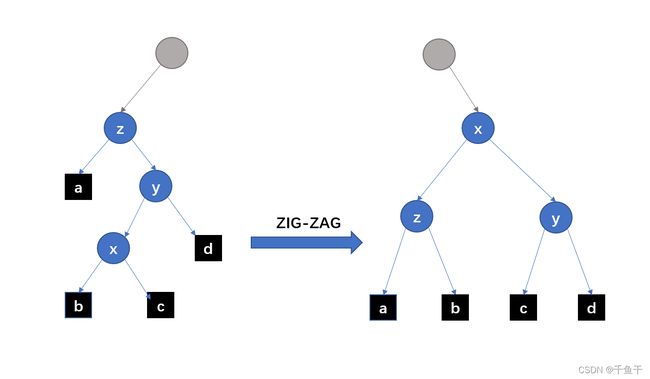
第三种：ZIG-ZAG / ZAG-ZIG

x的父结点y不是根节点，y的父结点为z，x与y中一个是其父结点的左孩子而另一个是其父结点的右孩子。此时进行一次Zig-Zag操作或者Zag-Zig操作。
以下图为例：
1.将z的右子树（以y为子树根结点）右旋，使x挂在原来y的位置上，此时y的左子树空缺，把x的右子树挂在y的左子树上；
2.将以z为根结点的子树左旋，使x挂在原来z的位置上，此时z的右子树空缺，把x的左子树挂在z的右子树即可。
注意：此时z结点不一定是根结点。

Splay树的伸展特性

Splay树的旋转能力会避免让BST成链表。
相对于Treap树的单旋，Splay树的双旋针对子结点、父结点、父结点的父结点在同一方向时会让树更加平衡。
比如在下图中，若结点通过两次单旋操作，把左图变成右图：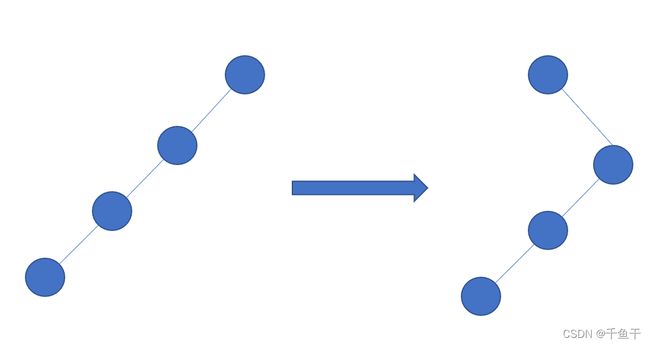
此时树的深度未改变，因此复杂度未变。
而通过双旋，此时左图变成右图的样子：
此时树的深度减小，树变得平衡，复杂度降低。

代码

了解了Splay树的基本原理后，我们将Splay树来实现进行各种操作，包括建树、插入、查找、删除等等，详细解释见我代码的注释。
注意：凡涉及查找结点操作的，都需要将被查找结点旋转至根结点。

前部分代码参考了书，后部分代码根据自己的理解编写，可能有误，谨慎使用，敬请批评指正！

完整代码

#include 

using namespace std;

const int maxn = 100010;
int root;  // 根结点

int fa[maxn], size[maxn];  // fa[i]: i 的父结点; size[i]: 以结 i 为根的子树的结点个数
int tree[maxn][2];         // tree[i][0]: i 的左孩子; tree[i][1]: i 的右孩子

// 求以结点 x 为根的子树的结点个数
void n_size(int x){
    size[x] = size[tree[x][0]] + size[tree[x][1]] + 1;
    // 最后加 1 因为自己也属于以自己为根的子树
}

// 以 x 为目标旋转。c = 0 左旋，c = 1 右旋
// 注: 以下代码建议结合 ZIG、ZAG 的那些图看。
void Rotate(int x, int c){
    int y = fa[x];
    tree[y][!c] = tree[x][c];
    fa[tree[x][c]] = y;
    if(fa[y]){
        tree[fa[y]][tree[fa[y]][1] == y] = x;
    }
    fa[x] = fa[y];
    tree[x][c] = y;
    fa[y] = x;
    n_size(y);
}

// 把 x 旋转为 goal 的儿子，如果 goal 是 0，则旋转为根
void splay(int x, int goal){
    while(fa[x] != goal){                     // 一直旋转，直到 x 成为 goal 的儿子
        if(fa[fa[x]] == goal){                // 情况1: x 的父结点是 goal 的儿子 ( 或根 ) ，单旋一次即可
            Rotate(x, tree[fa[x]][0] == x);
        }else{                                // x 的父结点不是 goal 的儿子 ( 或根 )
            int y = fa[x];
            int c = (tree[fa[y]][0] == y);
            if(tree[y][c] == x){              // 情况2: x、x 的父结点、x 父结点的父结点不共线
                Rotate(x, !c);
                Rotate(x, c);
            }else{                            // 情况3: x、x 的父结点、x 父结点的父结点不共线
                Rotate(y, c);
                Rotate(x, c);
            }
        }
    }
    n_size(x);
    if(goal == 0) root = x;                   // 如果 goal 是 0，则将根结点更新为 x
}

// 得到 以 x 为结点的子树上的最大值
// 后面也有个 get_max(), 那个是获得整棵树最大值，不要搞混！
int get_max(int x){
    while(tree[x][1]){
        x = tree[x][1];
    }
    return x;
}

// 删除结点
void del_root(){
    if(tree[root][0] == 0){
        root = tree[root][1];
        fa[root] = 0;
    }else{
        int m = get_max(tree[root][0]);
        splay(m, root);
        tree[m][1] = tree[root][1];
        fa[tree[root][1]] = m;
        root = m;
        fa[root] = 0;
        n_size(root);
    }
}

// 建立一个新结点
void newnode(int &x, int father, int val){
    x = val;
    fa[x] = father;
    size[x] = 1;
    tree[x][0] = tree[x][1] = 0;
}

// 建树用的代码
void buildtree(int &x, int l, int r, int father){
    if(l > r) return;
    int mid = (l + r)>>1;
    newnode(x, father, mid);
    buildtree(tree[x][0], l, mid - 1, x);
    buildtree(tree[x][1], mid + 1, r, x);
    n_size(x);
}

// 建树
void set_tree(int n){
    root = 0;
    tree[root][0] = tree[root][1] = fa[root] = size[root] = 0;
    buildtree(root, 1, n, 0);
}

// 中序遍历输出
void in_tree(int x){
    if(x == 0) return;
    in_tree(tree[x][0]);
    cout << x << " ";
    in_tree(tree[x][1]);
}

// 前序遍历输出
void pre_tree(int x){
    if(x == 0) return;
    cout << x << " ";
    pre_tree(tree[x][0]);
    pre_tree(tree[x][1]);
}

// 查找数 n 时用的前序遍历
void pre_tree(int x, int n, int &flag){
    if(x == 0) return;
    if(x == n) flag = (!flag);
    pre_tree(tree[x][0], n, flag);
    pre_tree(tree[x][1], n, flag);
}

// 查找是否存在数 n
bool find_n(int n){
    int flag = 0;
    pre_tree(root, n, flag);
    if(flag == 1){
        splay(n, 0);
        return true;
    }else{
        return false;
    }
}


// 删除数 n, n 存在删除 n 并返回true, n 不存在则返回 false
bool del_n(int n){
    if(find_n(n)){
        del_root();
        return true;
    }else{
        return false;
    }
}

// 查找整棵树最小值用的代码
int find_min(int x){
    if(tree[x][0] == 0){
        int temp = x;
        splay(x, 0);
        return temp;
    }else{
        find_min(tree[x][0]);
    }
}

// 查找整棵树最大值用的代码
int find_max(int x){
    if(tree[x][1] == 0){
        int temp = x;
        splay(x, 0);
        return temp;
    }else{
        find_max(tree[x][1]);
    }
}

// 查找整棵树第 k 大数时用的代码
void find_k(int x, int &k, int &m){
    if(x == 0) return;
    find_k(tree[x][0], k, m);
    k--;
    if(k == 0){
        m = x;
        splay(m, 0);
    }
    find_k(tree[x][1], k, m);
}

// 查找整棵树最小值
int get_min(){
    int minn = find_min(root);
    return minn;
}

// 查找整棵树最大值
int get_max(){
    int maxx = find_max(root);
    return maxx;
}

// 查找整棵树第 k 大值
int get_k_num(int k){
    int m = 0;
    find_k(root, k, m);
    return m;
}

int main(){
    int n;
    cout << "输入树结点个数：";
    cin >> n;
    set_tree(n);
    // 打印树的各节点信息
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    cout << endl;
    // 中序遍历，按从小到大打印各结点
    in_tree(root);
    cout << endl;
    // 前序遍历
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;

    // 查找数 f
    int f;
    cout << "输入待查找的数：";
    cin >> f;
    if(find_n(f) == true) cout << "存在" << endl;
    else cout << "不存在" << endl;
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    in_tree(root);
    cout << endl;
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;

    // 删除
    int d;
    cout << "输入待删除的数：";
    cin >> d;
    if(del_n(d) == true) cout << "删除成功！" << endl;
    else cout << "不存在" << endl;
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    in_tree(root);
    cout << endl;
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;

    // 查找最大、最小、第 k 大的数
    cout << "最大的数是：" << get_max() << endl;
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    in_tree(root);
    cout << endl;
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;

    cout << "最小的数是：" << get_min() << endl;
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    in_tree(root);
    cout << endl;
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;

    int k;
    cout << "输入待查的k：";
    cin >> k;
    cout << "第" << k << "大的数是：" << get_k_num(k) << endl;
    for(int i = 0; i <= n; i++){
        cout << "Node:" << i << " father:" << fa[i] << " lchild:" << tree[i][0] << " rchild:" << tree[i][1] << endl;
    }
    in_tree(root);
    cout << endl;
    pre_tree(root);
    cout << endl;
    cout << "root: " << root << endl;
    return 0;
}

总结

Splay树是一种结构简单、操作灵活的树（此处省略1000字）。。。
凌晨0点10分了，不能再说了，我要睡觉了，拜拜！