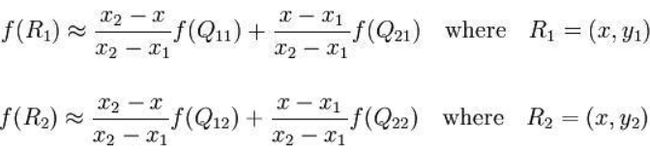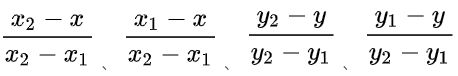双线性插值(Bilinear Interpol)原理及应用

在很多神经网络上采样过程中会用到双线性插值，其为基础的图像resize操作。以前一直没时间仔细研究，今天探究并记录一下原理和自己的理解。

一、什么是插值

插值指两个方面：

一是在数学上，在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点；

二是在图像处理上面，是利用已知邻近像素点的灰度值或RGB中的三色值产生未知像素点的灰度值或RGB三色值，目的是由原始图像再生出具有更高分辨率的图像。通俗一点理解就是已知推导未知，从而强化图像，具体效果如图1所示。

                                                                                           图1：插值示意图

当然，插值只是一个笼统的概念，利用怎样的规则进行插值才是重点。例如有最临近插值，双线性插值，高阶插值等等，今天主要解析一下双线性插值。

二、什么是线性插值

在研究双线性插值之前，首先看一下什么叫做线性插值。

线性插值是指插值函数为一次多项式的插值方式，其在插值节点上的插值误差为零。也就是连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的办法。

线性插值法是认为现象的变化发展是线性的、均匀的，所以可利用两点式的直线方程式进行线性插值。其几何意义可以示意为利用图中过A点和B点的直线来推断未知C点的坐标。

                                               图2：线性插值示意图:其中A坐标(x0,y0),B坐标(x1,y1)已知,求C(x,y)的y值

转换为公式计算（小写变大写，公式比较简单，懒得手打了）

单个维度的线性插值只利用两点的对应值推算，两点本身的偶然性会造成结果的误差较大，因而在图像处理中多采用双线性插值。

三、什么是双线性插值-数学理解

既然单个维度的线性插值误差较大，那么很自然的会想到从多维度的角度去减小误差，这就是双线性插值，其核心思想是在两个方向分别进行一次线性插值。

                                                                                  图3：双线性插值示意图

如图3中所示，我们的目标是得到未知函数f在绿色点P(x,y)的像素值，已知Q11(x1,y1)、Q12(x1,y2)、Q21(x2,y1)、Q22(x2,y2)的坐标以及对应的像素值。首先在x方向进行插值，得到R1和R2，然后在y方向进行插值，得到P，这就是整个的数学计算思路。

其中R1和R2的计算公式如下

通过在y方向插值，得到

代入和，得到最终像素值结果，最后式子比较复杂，但过程比较简单，可以自己推到一下，找找手感。

四、什么是双线性插值-图像处理

假设我们有一张大小为n*m的源图像，目标图像大小为a*b。那么两幅图像的边长比分别为：n/a和m/b。

注意，通常这个比例不是整数，编程存储的时候要用浮点型。

目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（i*n/a,j*m/b）。
显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。

双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。如果你的对应坐标是（2.5,4.5），那么最近的四个像素是(2,4)、(2,5)、(3,4)、(3,5)。若图像为灰度图像，那么（i,j）点的灰度值可以通过一下公式计算：
f(i,j)=w1*p1+w2*p2+w3*p3+w4*p4.
其中，pi(i=1,2,3,4)为最近的四个像素点，wi(i=1,2,3,4)为各点相应权值。

权值的计算公式如下

其实在上面已经出现过了。

五、遇到的问题（这部分直接引用现成的，文末有链接）

这部分的前提是，你已经明白什么是双线性插值并且在给定源图像和目标图像尺寸的情况下，可以用笔计算出目标图像某个像素点的值。当然，最好的情况是你已经用某种语言实现了网上一大堆博客上原创或转载的双线性插值算法，然后发现计算出来的结果和matlab、openCV对应的resize（）函数得到的结果完全不一样。

那这个究竟是怎么回事呢？

其实答案很简单，就是坐标系的选择问题，或者说源图像和目标图像之间的对应问题。

按照网上一些博客上写的，源图像和目标图像的原点（0,0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：

                                                                              图4：原点选择左上角示意图

只画了一行，用做示意，从图中可以很明显的看到，如果选择右上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。

那么，让坐标加1或者选择右下角为原点怎么样呢？很不幸，还是一样的效果，不过这次得到的图像将偏右偏下。

最好的方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。如下图：

                                                                                      图5：更改后示意图

如果你不懂我上面说的什么，没关系，只要在计算对应坐标的时候改为以下公式即可，

                                                                                      int x=(i+0.5)*n/a-0.5

                                                                                      int y=(j+0.5)*m/b-0.5

代替

                                                                                              int x=i*n/a

                                                                                              int y=j*m/b

利用上述公式，将得到正确的双线性插值结果

 

六、最后附上两端代码（同为引用，仅供参考）

for n in range(3): # 对channel循环
        for dst_y in range(dst_h): # 对height循环
            for dst_x in range(dst_w): # 对width循环
                # 目标在源上的坐标
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
                # 计算在源图上四个近邻点的位置
                src_x_0 = int(np.floor(src_x))
                src_y_0 = int(np.floor(src_y))
                src_x_1 = min(src_x_0 + 1, src_w - 1)
                src_y_1 = min(src_y_0 + 1, src_h - 1)

                # 双线性插值
                value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, n] + (src_x - src_x_0) * src[src_y_0, src_x_1, n]
                value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, n] + (src_x - src_x_0) * src[src_y_1, src_x_1, n]
                dst[dst_y, dst_x, n] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)
    return dst

uchar* dataDst = matDst1.data;
    int stepDst = matDst1.step;
    uchar* dataSrc = matSrc.data;
    int stepSrc = matSrc.step;
    int iWidthSrc = matSrc.cols;
    int iHiehgtSrc = matSrc.rows;

    for (int j = 0; j < matDst1.rows; ++j)
    {
        float fy = (float)((j + 0.5) * scale_y - 0.5);
        int sy = cvFloor(fy);
        fy -= sy;
        sy = std::min(sy, iHiehgtSrc - 2);
        sy = std::max(0, sy);

        short cbufy[2];
        cbufy[0] = cv::saturate_cast((1.f - fy) * 2048);
        cbufy[1] = 2048 - cbufy[0];

        for (int i = 0; i < matDst1.cols; ++i)
        {
            float fx = (float)((i + 0.5) * scale_x - 0.5);
            int sx = cvFloor(fx);
            fx -= sx;

            if (sx < 0) {
                fx = 0, sx = 0;
            }
            if (sx >= iWidthSrc - 1) {
                fx = 0, sx = iWidthSrc - 2;
            }

            short cbufx[2];
            cbufx[0] = cv::saturate_cast((1.f - fx) * 2048);
            cbufx[1] = 2048 - cbufx[0];

            for (int k = 0; k < matSrc.channels(); ++k)
            {
                *(dataDst+ j*stepDst + 3*i + k) = (*(dataSrc + sy*stepSrc + 3*sx + k) * cbufx[0] * cbufy[0] + 
                    *(dataSrc + (sy+1)*stepSrc + 3*sx + k) * cbufx[0] * cbufy[1] + 
                    *(dataSrc + sy*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[0] + 
                    *(dataSrc + (sy+1)*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[1]) >> 22;
            }
        }
    }
    cv::imwrite("linear_1.jpg", matDst1);

    cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 1);
    cv::imwrite("linear_2.jpg", matDst2);

参考链接：

https://www.cnblogs.com/yibeimingyue/p/11485732.html

https://blog.csdn.net/sinat_33718563/article/details/78825971

https://zhuanlan.zhihu.com/p/49832888

https://blog.csdn.net/qq_37577735/article/details/80041586

https://blog.csdn.net/xbinworld/article/details/65660665