深度强化学习_AlphaGo 王树森课程笔记

深度强化学习实例：围棋游戏

一、 游戏规则

棋盘：19x19

落子点：361个

State：黑白棋子以及空位的排列。

状态 $s$：可以用由0和1组成的19x19x2的tensor来表示。

• 分别用两个19x19的矩阵来对应黑子和白子，若某位置有黑子（白子），矩阵对应元素为1，否则为0；
• AlphaGo实际使用19x19x48的tensor来记录其他信息。

Action：往棋盘的空白位置上放一个棋子。

• 动作空间 Action space：$\mathcal{A}\subset \{1,2,3,\dots ,361\}$。

二、 设计思路

Training

1. 用behavior cloning来初步学习策略网络（policy network）：AlphaGo从16万局人类的游戏记录中学习一个策略网络；
   a. behavior cloning：一种监督学习，本质是多分类，不是强化学习。
2. 用策略梯度算法训练策略网络：AlphaGo用两个策略网络做自我博弈，拿胜负结果来训练策略网络；
3. 用策略网络训练价值网络（value network）。（实质是在做回归）
   a. 用的不是actor-critic方法，actor-critic方法要求同时训练策略网络和价值网络，而AlphaGo先训练策略网络后训练价值网络。

Execution

用策略网络和价值网络执行蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）

三、 Training

1. 策略网络

1.1 State (of AlphaGo Zero)

19x19x17的tensor：

• 19x19：对应黑子（白子），若某位置有黑子（白子），矩阵对应元素为1，否则为0；
• 17：把当前黑子的位置用一个矩阵表示，之前七步黑子的位置用另外七个矩阵表示，为了表示最近八步黑子和白子的位置需要用到8+8=16个矩阵；第17个矩阵：如果当前该下黑子，则为全1矩阵，若该下白子则为全0矩阵。
  

1.2 Policy Network

Policy Network of AlphaGo

状态：由19x19x48的tensor表示。

策略网络：都是卷积层，没有全连接层。

输出：19x19的矩阵，矩阵每一个元素对应一个放棋子的位置，即输出361个动作的概率。

Policy Network of AlphaGo Zero

状态：由19x19x17的tensor表示，作为输入。

输出：361维的向量，输出层的激活函数是softmax（输出的是概率分布）

1.3 Behavior Cloning

训练第一步：用Behavior Cloning初始化策略网络，从人的经验中学习一个初步的策略网络。
 AlphaGo 2016用了Behavior Cloning，AlphaGo Zero没用到。

• 原因：开始时，策略网络的参数由随机初始化得到。（若直接让策略网络自我博弈，它们需要随机摸索很多次才能得出合理的动作，时间消耗太大）
• 训练数据：人类围棋游戏动作序列被记录下来。（KGS有160k局高级玩家游戏记录）
• Behavior Cloning：用监督学习的方法训练策略网络。
• 训练后的策略网络足以打败业余玩家，打不过职业玩家。

Behavior Cloning不是强化学习，而是一种模仿学习（Imitation learning），agent不需要奖励，只需要模仿人的动作就行。是一种多分类回归方法。

强化学习与模仿学习的本质区别：是否有奖励。

用Behavior Cloning训练策略网络

1. 每一步观测到一个状态$s_t$（用一个tensor表示棋盘格局），作为策略网络$\pi$的输入；
2. 策略网络给出预测（361维的向量）$p_t=[\pi (1|s_t,\mathbf{\theta }),\dots ,\pi (361|s_t,\mathbf{\theta })]\in (0,1{)}^{361}$，表示361个动作的概率；
3. 人类玩家真实动作$a_t^{\ast }=281$，即把棋子下在第281号位置；
4. 将动作$a_t^{\ast }=281$做one-hot encode，得到一个361维向量 $y_t\in \{0,1{\}}^{361}$（第281个元素是1，其余全零）；
5. Loss=CrossEntropy$(y_t,p_t)$，用CrossEntropy作为损失函数，衡量人类玩家的动作$y_t$与策略网络的预测$p_t$之间的差异，$y_t$与$p_t$越接近，CorssEntropy就越小；
6. 求损失函数关于神经网络参数$\mathbf{\theta }$的梯度，做梯度下降更新$\mathbf{\theta }$。

Behavior Cloning本质是多分类

• 棋盘上有361个位置：361个类别；
• 策略网络的输出：每一个类别的概率；
• 人类玩家的动作：361个类别中的一个，看作是ground truth，即真实标签。

缺点

若状态$s_t$没有出现在训练数据中，则策略网络做出的决策$a_t$就不会太好，导致出现下一个训练数据未包含的状态，从而使得策略网络生成更离谱的动作，随着错误累加，状态会越来越奇怪，策略网络做出更糟糕的动作，最后AI失败。

改进

在Behavior Cloning后用强化学习接着训练策略网络，让策略网络变得更强大。

1.4 策略梯度

用策略梯度算法进一步提高策略网络。

用强化学习训练策略网络——两个策略网络做博弈

• Player：即Agent，由策略网络控制，用的是策略网络最新的模型参数，每下完一局围棋，把胜负作为奖励，靠奖励更新Player参数。
• Opponent：即Environment，每当Player下一个棋子，Opponent也走一步，相当于随机状态转移，用策略网络控制，随机从旧的参数中选一个出来作为Opponent参数。

定义奖励：假设step $T$后一局游戏结束

奖励：

• $r_1=r_2=\cdots =r_{T-1}=0$（一局游戏没结束时奖励都为0）；
• $r_T=+1$（winner）；
• $r_T=-1$（loser）。

回报：

• $u_t={\sum }_{i=t}^T{r}_i$（不做折扣）；
• Winner：$u_1=u_2=\cdots =u_T=+1$；Agent获胜，认为Agent所有动作都是好的；
• Loser：$u_1=u_2=\cdots =u_T=-1$；Agent失败，认为Agent每一步动作都是臭棋。
• 即无法区分具体哪一个动作的好坏，只能把每步都同等对待，用最终结果给所有动作相同的回报。

Policy Gradient

Policy Gradient：状态价值函数$V(s;\mathbf{\theta })$关于策略网络参数$\mathbf{\theta }$的梯度。

• 用策略梯度的无偏估计$\frac{\partial \log \pi (a_t|s_t;\mathbf{\theta })}{\partial \mathbf{\theta }}\cdot Q_{\pi }(s_t,a_t)$近似策略梯度；
• 动作价值函数定义为随机变量$U_t$的条件期望：$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t]$；
• 可以用$U_t$的观测值$u_t$来近似$U_t$的期望，即用$u_t$来近似$Q_{\pi }(s_t,a_t)$；
• 近似策略梯度：$\frac{\partial \log \pi (a_t|s_t;\mathbf{\theta })}{\partial \mathbf{\theta }}\cdot u_t$。

总体流程

• Player和Opponent博弈，每玩完一局可更新一次模型参数；
• 得到轨迹：$s_1,a_1,\dots ,s_T,a_T$；
• 得到轨迹和奖励后，更新Player的策略网络：
  • Player回报：$u_1=u_2=\cdots =u_T$（均为+1或-1）；
  • 计算近似策略梯度的累加和：${\text{g}}_{\theta }={\sum }_{t=1}^T\frac{\partial \log \pi (a_t|s_t;\mathbf{\theta })}{\partial \mathbf{\theta }}\cdot u_t$；
  • 策略梯度上升，更新策略网络：$\mathbf{\theta }\leftarrow \mathbf{\theta }+\beta \cdot {\text{g}}_{\theta }$。

2. 价值网络

此处的价值网络是对状态价值函数$V$的近似，而不是对$Q^{\ast }$的近似。

AlphaGo用价值网络$v(s,\text{w})$近似价值函数$V_{\pi }(s)$，用价值网络评价当前状态的好坏。

• 状态价值函数：$V_{\pi }(s)=\mathbb{E}[U_t|S_t=s]$，其中$U_t$为+1或-1。
• 给定策略函数$\pi$，状态价值函数$V_{\pi }$可以评价当前状态$s$的好坏，值越接近1，状态越好越接近胜利；值接近-1则代表快输了。

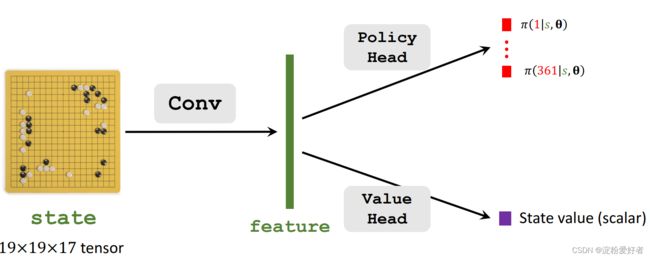
2.1 Policy Value Networks (AlphaGo Zero)

AlphaGo：策略网络和价值网络是分开的两个神经网络；

AlphaGo Zero：策略网络和价值网络共享一些卷积层：

输入：两个网络都需要将19x19x17的状态tensor作为输入；

卷积：底层卷积对输入提取特征，提取到的特征对两个网络都适用。

输出：

• 策略网络：输出361个概率值，每个值对应一个动作（即棋盘上的位置），说明了下一步该怎么走。
• 价值网络：输出一个标量，是对当前状态$s$的打分，反映出当前状态下的胜算有多大。

2.2 训练价值网络

AlphaGo先训练策略网络$\pi$，然后在策略网络的帮助下训练价值网络$v$。

1. 让两个策略网络进行博弈，每下完一局更新一次价值网络，并得到回报$u_t$；（用到策略网络）

   Winner：$u_1=u_2=\cdots =u_T=+1$；

   Loser：$u_1=u_2=\cdots =u_T=-1$；

2. Loss：$L={\sum }_{t=1}^T\frac{1}{2}[v(s_t,\text{w})-u_t{]}^2$；$L$可以反映出价值网络$v$的预测是否准确，预测越准值越小；

   价值网络$v$的学习可类比于回归问题：将真实观测到的$u_t$作为target，希望价值网络的预测$v(s_t,\text{w})$与真实值$u_t$接近。

3. 做梯度下降更新模型参数：$\text{w}\leftarrow \text{w}-\alpha \cdot \frac{\partial L}{\partial \text{w}}$。

四、 Execution：Monte Carlo Tree Search

下棋时需要向前看n步，模拟未来情况，从而挑选出当前最优动作，穷举出的情况越多胜算越大。

1. 主要思想

1. 随机抽取动作$a$：按照动作的好坏程度，以不同的概率选择；排除掉不好的动作，只搜索好的动作；

   用策略函数排除掉不好的动作：策略函数可以算出每个动作的概率值，概率值非常低的都是不好的动作，都要排除掉。

2. 用策略网络做自我博弈直至游戏结束，看胜负结果，并根据胜负情况和价值函数来给动作$a$打分；

3. 重复2多次，每个动作都有很多分数，分数反映动作好坏；

4. AlphaGo执行总分最高的动作。

2. MCTS步骤

蒙特卡洛树搜索每轮模拟分四步（AlphaGo每下一步棋子都要把这四步模拟重复多次）：

1. Selection：按照动作的分数选出一个动作$a$（该动作为假象动作，AlphaGo并不真正执行）进行模拟，看看这个动作好不好；
2. Expansion：假象对手根据策略网络$\pi$随机走一步（同样为模拟），并更新状态；
3. Evaluation：给本次选出的动作$a$打分；价值网络给当前状态打分为$v$，策略网络做自我博弈直到游戏结束得到奖励$r$。动作$a$的分数为$\frac{v+r}{2}$；
4. Backup：用计算出的数值$\frac{v+r}{2}$更新动作的分数。

2.1 Step1：Selection

【问题】观测到棋盘状态$s_t$，应该探索哪一个动作？
  【策略】应该优先探索好的动作，可以忽略掉不好的动作。

• 首先给所有动作$a$打分：$\text{score}(a)=Q(a)+\eta \cdot \frac{\pi (a|s_t;\mathbf{\theta })}{1+N(a)}$；反映动作的好坏程度，好的动作分数高。

  初始化时，所有$Q(a)$都为0，完全由策略网络$\pi$决定探索哪个动作；多次搜索后，$N(a)$变大，第二项值变小，策略网络变得无关紧要，此时探索哪一个动作几乎完全由$Q(a)$来决定。

  • $Q(a)$：动作价值（一张表，记录了361个动作的分数），由MCTS计算得到；
  • $\eta$：超参数，需手动调整；
  • $\pi (a|s_t;\mathbf{\theta })$：策略网络；
  • $N(a)$：给定状态$s_t$，动作$a$被选中的次数；
  • $\frac{\pi (a|s_t;\mathbf{\theta })}{1+N(a)}$：动作越好，策略网络$\pi$给$a$打的分数就会越高，分子$\pi (a|s_t;\mathbf{\theta })$越大；但若动作$a$已经被多次探索，分母中的$N(a)$就会变大，降低动作$a$的分数，如此可避免重复探索同一个动作太多次；

• 选择分数最高的动作进行探索，并更新该动作的分数。

2.2 Step2：Expansion

【问题】假如AlphaGo执行上步选中的动作$a_t$后，对手会做什么动作？

• 假设AlphaGo执行选定动作$a_t$，用策略网络模拟对手：根据策略网络随机抽样一个动作$a_t^{\prime }\sim \pi (\cdot |s_t^{\prime };\mathbf{\theta })$，并假设对手执行该动作；

  $s_t^{\prime }$：站在对手角度观测到的棋盘状态；

• 对手执行动作$a_t^{\prime }$后，产生新的状态$s_{t+1}$。

  • 对手相当于环境，对手的策略相当于状态转移函数$p(s_{t+1}|s_t,a_t)$，即对手的动作会产生新的状态$s_{t+1}$；
  • 状态转移函数未知，可以拿策略函数$\pi$代替。

2.3 Step3：Evaluation

• Fast Rollout：从状态$s_{t+1}$开始，让策略网络做自我博弈，直到分出胜负为止；
• 一局结束后得到奖励$r_T$，用来评价状态$s_{t+1}$的好坏，赢了便增加$s_{t+1}$的评分，若输了便减少$s_{t+1}$的评分；
• 用价值网络$v$评价$s_{t+1}$：直接把$s_{t+1}$输入价值网络得到分数$v(s_{t+1};\text{w})$；
• 计算出状态$s_{t+1}$的分数：$V(s_{t+1})=\frac{1}{2}v(s_{t+1};\text{w})+\frac{1}{2}{r}_T$，反映出状态$s_{t+1}$的好坏。

2.4 Step4：Backup

• MCTS会重复很多次，每个状态下都会有多条记录，每个动作$a_t$都有很多个子节点$V(s_{t+1})$；
• 将$a_t$下的所有记录做平均作为$a_t$新的价值$Q(a_t)$，是对动作$a_t$好坏的评价；
  • $Q$在第一步Selection被用到：初始化时所有$Q$都为0，每当一个动作被搜索一次就会留下一条记录，$Q$值是所有记录$V$值的平均。

3. 决策

• $N(a)$可以反映出动作的好坏：一个动作越好，被选中的次数就越多，即一个动作$a$的$Q$值和$\pi$值越大，$N(a)$就越大。
• MCTS后做出决策：选中$N$值最大的动作并执行，即$a_t=\underset{a}{\mathrm{argmax}}N(a)$。