典型相关分析笔记
典型相关分析 什么时候用?
典型相关分析 的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量,利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性
典型相关分析 非常适合在题目要求分析两组数据(每组数据间有多个指标)之间的关系时使用
典型相关分析的顺序
① 数据分布的假设(预处理)
② 对变量相关性检验(假设检验)
③ 标准化典型相关变量(做出典型相关模型)
④ 典型载荷分析(进一步对数据分析)
典型相关分析的例题演示
我们要探究观众和业内人士对于一些电视节目的观点有什么样的关系呢?
【资料:观众评分来自 低学历(Ied)、高学历(hed) 和 网络调查(net) 三种,形成第一组变量;而业内人士分评分来自包括演员和导演在内的 艺术家(arti)、发行(com) 与 业内人士(man) 三种,形成第二组变量】
一、数据分布的假设
为研究观众与业内人士这两类人群对电视节目的观点的相关性,令观众与业内人士的评分为两组样本数据,采用典型相关分析法,分别在第一组变量与第二组变量中,找到一组线性组合,使得其相关系数最大
设 X = [ X ( 1 ) X ( 2 ) ] \mathbf{X}=\left[\begin{array}{l} \mathbf{X}^{(1)} \\ \mathbf{X}^{(2)} \end{array}\right] X=[X(1)X(2)] 服从正态分布 N 3 + 3 ( μ , Σ ) N_{3+3}(\boldsymbol{\mu}, \boldsymbol{\Sigma}) N3+3(μ,Σ),从整体中抽取样本容量为 30 30 30 的样本,得到下列数据矩阵:
X ( 1 ) = [ X 1 , 1 ( 1 ) X 1 , 2 ( 1 ) X 1 , 3 ( 1 ) X 2 , 1 ( 1 ) X 2 , 2 ( 1 ) X 2 , 3 ( 1 ) ⋮ ⋮ ⋮ X 30 , 1 ( 1 ) X 30 , 2 ( 1 ) X 30 , 3 ( 1 ) ] \mathbf{X}^{(1)}=\left[\begin{array}{cccc} X_{1,1}^{(1)} & X_{1,2}^{(1)} & X_{1,3}^{(1)} \\ X_{2,1}^{(1)} & X_{2,2}^{(1)} & X_{2,3}^{(1)} \\ \vdots & \vdots & \vdots \\ X_{30,1}^{(1)} & X_{30,2}^{(1)} & X_{30,3}^{(1)} \end{array}\right] X(1)=⎣⎢⎢⎢⎢⎡X1,1(1)X2,1(1)⋮X30,1(1)X1,2(1)X2,2(1)⋮X30,2(1)X1,3(1)X2,3(1)⋮X30,3(1)⎦⎥⎥⎥⎥⎤ X ( 2 ) = [ X 1 , 1 ( 2 ) X 1 , 2 ( 2 ) X 1 , 3 ( 2 ) X 2 , 1 ( 2 ) X 2 , 2 ( 2 ) X 2 , 3 ( 2 ) ⋮ ⋮ ⋮ X 30 , 1 ( 2 ) X 30 , 2 ( 2 ) X 30 , 3 ( 2 ) ] \mathbf{X}^{(2)}=\left[\begin{array}{cccc} X_{1,1}^{(2)} & X_{1,2}^{(2)} & X_{1,3}^{(2)} \\ X_{2,1}^{(2)} & X_{2,2}^{(2)} & X_{2,3}^{(2)} \\ \vdots & \vdots & \vdots \\ X_{30,1}^{(2)} & X_{30,2}^{(2)} & X_{30,3}^{(2)} \end{array}\right] X(2)=⎣⎢⎢⎢⎢⎡X1,1(2)X2,1(2)⋮X30,1(2)X1,2(2)X2,2(2)⋮X30,2(2)X1,3(2)X2,3(2)⋮X30,3(2)⎦⎥⎥⎥⎥⎤
然后对样本数据进行标准化处理,得到的样本的相关系数矩阵 R ^ \hat{R} R^ :
R ^ = [ R ^ 11 R ^ 12 R ^ 21 R ^ 22 ] \hat{R}=\left[\begin{array}{cc} \hat{R}_{11} & \hat{R}_{12} \\ \hat{R}_{21} & \hat{R}_{22} \end{array}\right] R^=[R^11R^21R^12R^22]由此可得矩阵 A A A 和 B B B 的样本估计:
A ^ ∗ = R ^ 11 − 1 R ^ 12 R ^ 22 − 1 R ^ 21 \hat\mathbf{A}^{*}=\hat{\mathbf{R}}_{11}^{-1} \hat{\mathbf{R}}_{12} \hat{\mathbf{R}}_{22}^{-1} \hat{\mathbf{R}}_{21} A^∗=R^11−1R^12R^22−1R^21 B ^ ∗ = R ^ 22 − 1 R ^ 21 R ^ 11 − 1 R ^ 12 \hat\mathbf{B}^{*}=\hat{\mathbf{R}}_{22}^{-1} \hat{\mathbf{R}}_{21} \hat{\mathbf{R}}_{11}^{-1} \hat{\mathbf{R}}_{12} B^∗=R^22−1R^21R^11−1R^12
求解 A ^ ∗ \hat\mathbf{A}^{*} A^∗ 和 B ^ ∗ \hat\mathbf{B}^{*} B^∗ 的特征根及相应的特征向量,即可得到典型变量及典型相关系数,最终根据典型相关系数得到我们的典型相关分析表达式
二、确定典型相关变量的个数并进行假设检验
下图是我们要分析的两组变量指标
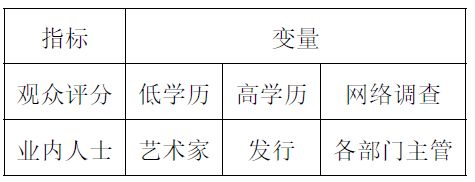
根据样本数据检验总体典型相关系数 λ 1 、 λ 2 、 λ 3 λ_1、λ_2、λ3 λ1、λ2、λ3,对变量进行相关性检验(假设检验):
原假设 H 0 H_0 H0 : λ 1 = λ 2 = λ 3 = 0 λ_1=λ_2=λ3=0 λ1=λ2=λ3=0
备择假设 H 1 H_1 H1 :至少有一个不为 0 0 0
将数据导入 SPSS 软件中,对观众与业内人士对节目的评分的两组样本数据进行典型性分析,得到如下结果:
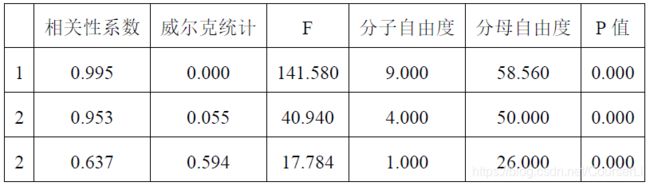
从上表可知,三组典型相关变量之间的 P P P 值都很小,接近于 0 0 0(小于 0.05 0.05 0.05 ),在 99% 的置信水平下,拒绝原假设 H 0 H_0 H0,即认为典型相关系数显著,说明观众与业内人士之间存在着显著的正向相关关系。并由表可见,第一、第二对典型变量之间的典型相关系数 λ 1 、 λ 2 λ_1、λ_2 λ1、λ2 都大于 0.9 0.9 0.9,由此可见这两对典型变量的解释能力较强,并且相应典型变量之间密切相关
对典型变量进行 冗宇分析 得到 已解释的方差比例表格,如下所示:

由表可知,对于集合 1 与 集合 2,前两组典型相关变量的自身解释量分别高达 0.893 0.893 0.893 和 0.969 0.969 0.969,因此,只需要选取的两对典型相关变量,就可以完整的阐述整体原数据的关系
三、利用标准化后的典型相关变量分析问题
观众与业内人士对节目的评分的典型相关变量对应的线性组合分别如下所示:
观众评分标准化典型相关系数表:

业内人士评分标准化典型相关系数表:
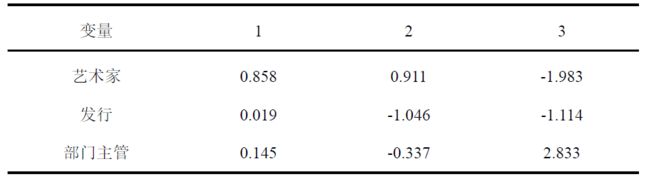
从而得到典型相关数向量:
a ( 1 ) ∗ = ( 0.149 , 0.977 , − 0.052 ) ′ \mathbf{a}^{(1)^{*}}=(0.149,0.977,-0.052)^{\prime} a(1)∗=(0.149,0.977,−0.052)′
a ( 2 ) ∗ = ( − 0.786 , 0.383 , − 0.312 ) ′ \mathbf{a}^{(2) *}=(-0.786,0.383,-0.312)^{\prime} a(2)∗=(−0.786,0.383,−0.312)′
b ( 1 ) ∗ = ( 0.858 , 0.019 , 0.145 ) ′ \mathbf{b}^{(1)^{*}}=(0.858,0.019,0.145)^{\prime} b(1)∗=(0.858,0.019,0.145)′
b ( 2 ) ∗ = ( 0.911 , − 1.046 , − 0.337 ) ′ \mathbf{b}^{(2) *}=(0.911,-1.046,-0.337)^{\prime} b(2)∗=(0.911,−1.046,−0.337)′
最终得到相关检验模型,为了便于比较,我们选用对典型系数标准化后的典型相关模型:
【操作: 这个表格我是用 Word 做的,相比 Latex 制作要简单点】
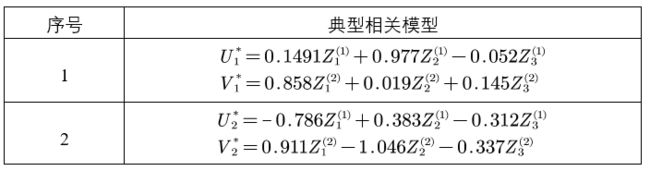
注:其中 Z i ( 1 ) Z_{i}^{(1)} Zi(1)和 Z j ( 2 ) Z_{j}^{(2)} Zj(2)分别为原始变量 X i ( 1 ) X_{i}^{(1)} Xi(1)和 Y i ( 2 ) Y_{i}^{(2)} Yi(2)是标准化后的结果
以上结果说明,典型变量 U 1 ∗ U_1^* U1∗ 相对于第一个特征值, Z 2 Z_2 Z2(高学历) 的重要程度最大,即 U 1 ∗ U_1^* U1∗ 主要代表着 高学历(hed) 变量并呈正相关。同理可得, U 2 ∗ U_2^* U2∗ 主要代表着 低学历(led) 变量并呈负相关 、 V 1 ∗ V_1^* V1∗ 主要代表着 艺术家(art) 变量并呈正相关 、 V 2 ∗ V_2^* V2∗ 主要代表着 发行(com) 变量并呈负相关
四、进行典型载荷分析
观众与业内人士两组数据的典型相关变量的典型载荷分别如下所示:
观众评分典型载荷:

由上表可见普通观众的第一变量与低学历人群的相关系数为 0.333 0.333 0.333,与高学历人群的相关系数为 0.933 0.933 0.933,与网络用户的相关系数为 0.383 0.383 0.383,另一方面也说明了第一变量与三个群体均呈正相关。第二变量与低学历人群的相关系数为 − 0.925 -0.925 −0.925,与网络用户的相关系数为 − 0.753 -0.753 −0.753,其中与低学历人群的相关性最高为 − 0.925 -0.925 −0.925,另一方面也说明了第二变量与低学历人群和网络用户成负相关。此外,第一变量主要反映的是高学历人群,第二变量主要反映网络用户和低学历人群
业内人士评分典型载荷:
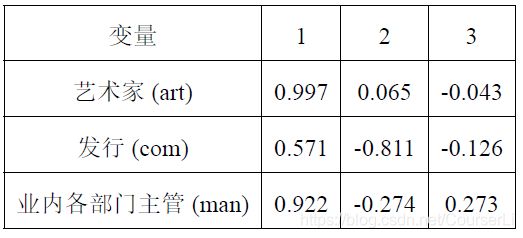
由上表可知业内人士的第一变量与艺术家人群的相关系数为 0.997 0.997 0.997,与发行商人群的相关系数为 0.571 0.571 0.571,与主管的相关系数为 0.922 0.922 0.922,另一方面也说明了第一变量与三个群体均呈正相关。第二变量与高学历人群的相关系数为 − 0.811 -0.811 −0.811,与发行商的相关系数为 − 0.274 -0.274 −0.274,另一方面也说明了第二变量与发行商和主管成负相关。此外,第一变量主要反映的是艺术家,第二变量主要反映发行商
典型相关分析的补充
不同于相关性分析,典型相关分析本身就是一个模型,类似于 皮尔逊相关系数模型 和 斯皮尔曼相关系数模型
典型相关分析的评估
典型相关分析 的优点:
(1) 能良好的反应出两组变量的指标之间多对多联系
(2) 可推广性很强
典型相关分析 的缺点:
在解决时间序列问题时存在不足,不能及时、准确地反映样本数据的时间特征及变化趋势