MATLAB - 模糊控制入门教程（Fuzzy Logic control）

系列文章目录

---

---

一、什么是模糊控制？

1.1 模糊逻辑描述

近年来，模糊逻辑的应用数量和种类大幅增加。应用范围从照相机、摄像机、洗衣机和微波炉等消费产品，到工业过程控制、医疗仪器、决策支持系统和组合选择。

要了解模糊逻辑的应用为何不断增长，首先必须了解模糊逻辑的含义。

模糊逻辑有两种不同的含义。从狭义上讲，模糊逻辑是一种逻辑系统，是多值逻辑的延伸。然而，从广义上讲，模糊逻辑（FL）几乎是模糊集合理论的同义词，这种理论涉及没有明确界限的对象类别。在这种情况下，集合中的成员资格是一个程度问题。从这个角度看，狭义的模糊逻辑是 FL 的一个分支。即使从狭义上讲，模糊逻辑在概念和实质上都不同于传统的多值逻辑系统。

在 Fuzzy Logic Toolbox™ 软件中，模糊逻辑应被解释为 FL，即广义的模糊逻辑。模糊逻辑的基本思想已在《模糊逻辑基础》中作了解释。需要补充的是，FL 的基本概念是语言变量，即变量值是文字而不是数字。实际上，FL 的大部分内容都可以看作是一种用文字而不是数字进行计算的方法。虽然文字在本质上不如数字精确，但文字的使用更接近人类的直觉。此外，用文字计算还能利用对不精确的容忍度，从而降低解决问题的成本。

模糊语言的另一个基本概念是模糊 "如果-那么 "规则，或简称为模糊规则，它在大多数应用中都发挥着核心作用。虽然基于规则的系统在人工智能（AI）领域的应用由来已久，但这类系统缺少的是处理模糊结果和模糊前因的机制。在模糊逻辑中，这种机制由模糊规则微积分提供。模糊规则计算是模糊依存和命令语言（FDCL）的基础。虽然 FDCL 在工具箱中没有明确使用，但它实际上是工具箱的主要组成部分之一。在模糊逻辑的大多数应用中，模糊逻辑解决方案实际上就是将人类解决方案转换成 FDCL。

一个日益引人注目的趋势是将模糊逻辑与神经计算和遗传算法结合起来使用。更广泛地说，模糊逻辑、神经计算和遗传算法可被视为软计算的主要组成部分。与传统的硬计算不同，软计算考虑到了现实世界的不确定性。软计算的指导原则是 利用对不精确性、不确定性和部分真实性的容忍度来实现可操作性、鲁棒性和低解决成本。未来，在构思和设计 MIQ（机器智商）远高于传统方法设计的系统时，软计算将发挥越来越重要的作用。

在软计算的各种方法组合中，目前最引人注目的是模糊逻辑和神经计算的组合，从而产生了神经模糊系统。在模糊逻辑中，这种系统在从观察结果中归纳出规则方面发挥着特别重要的作用。Roger Jang 博士为此开发的一种有效方法被称为 ANFIS（自适应神经模糊推理系统）。这种方法是工具箱的重要组成部分。

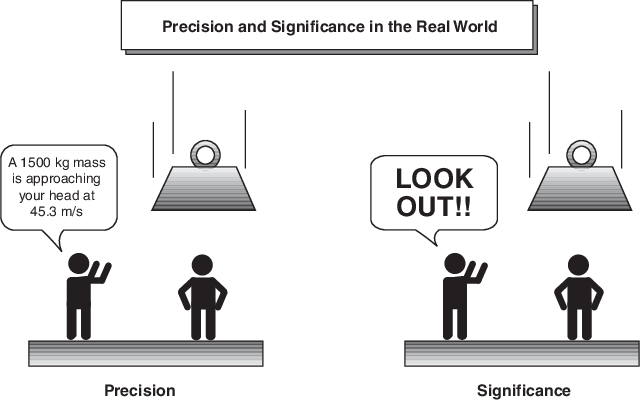
模糊逻辑近似于人类推理，能很好地平衡精确度和重要性之间的权衡。例如，当警告某人有物体向其坠落时，并不需要精确到确切的质量和速度。

模糊逻辑是将输入空间映射到输出空间的一种便捷方法。请看下面的例子。

• 模糊逻辑系统可以根据您在餐馆的服务质量信息，告诉您小费应该是多少。

• 根据您对水温的要求，模糊逻辑系统可以将水龙头阀门调节到合适的温度。

• 模糊逻辑系统可以根据拍摄对象距离多远的信息，为你调整镜头焦距。

• 有了汽车行驶速度和马达工作强度的信息，模糊逻辑系统就能为你换挡。

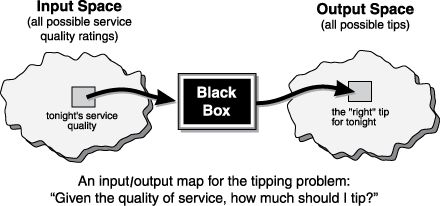
模糊系统就像一个将输入空间映射到输出空间的黑盒子。例如，您可以将所有可能的餐厅服务评级的输入空间映射到所有可能的小费值。

确定适当的提示量需要将输入映射到适当的输出。在输入和输出之间，上图显示了一个黑盒子，黑盒子里可以包含任何东西：模糊系统、线性系统、专家系统、神经网络、微分方程、内插多维查找表，甚至是精神导师，这只是其中几个可能的选项。显然，这个清单可以一直列下去。

在几十种让黑盒子工作的方法中，模糊往往是最好的方法。为什么会这样呢？被誉为 "模糊逻辑之父 "的 Lotfi Zadeh 曾经说过： “几乎在所有情况下，不使用模糊逻辑也能制造出同样的产品，但模糊逻辑更快、更便宜”。

1.2 为什么使用模糊逻辑？

以下是关于模糊逻辑的一般看法：

• 模糊逻辑在概念上易于理解。

  模糊推理背后的数学概念非常简单。模糊逻辑是一种更直观的方法，没有深远的复杂性。

• 模糊逻辑具有灵活性。

  对于任何给定的系统，都可以很容易地叠加更多的功能，而无需从头开始。

• 模糊逻辑能够容忍不精确的数据。

  如果你仔细观察，任何事物都是不精确的，不仅如此，即使仔细观察，大多数事物也是不精确的。模糊推理将这种理解融入到整个过程中，而不是将其附加到最后。

• 模糊逻辑可以模拟任意复杂的非线性函数。

  你可以创建一个模糊系统来匹配任何一组输入输出数据。模糊逻辑工具箱软件中的自适应神经模糊推理系统（ANFIS）等自适应技术使这一过程变得尤为简单。

• 模糊逻辑可以建立在专家经验的基础上。

  神经网络会获取训练数据并生成不透明、难以捉摸的模型，与之形成鲜明对比的是，模糊逻辑可以让你依靠那些已经了解你的系统的人的经验。

• 模糊逻辑可与传统控制技术相融合。

  模糊系统并不一定要取代传统的控制方法。在许多情况下，模糊系统可以增强传统控制方法，并简化其实施过程。

• 模糊逻辑基于自然语言。

  模糊逻辑的基础就是人类交流的基础。这一观点是其他许多关于模糊逻辑的论述的基础。由于模糊逻辑建立在日常语言的定性描述结构之上，因此模糊逻辑易于使用。

最后一句话也许是最重要的一句话，值得更多讨论。普通人每天都在使用的自然语言，经过人类几千年的历史演变，已经变得方便、高效。用普通语言写成的句子代表了高效交流的胜利。

1.3 何时不使用模糊逻辑？

什么时候不应该使用模糊逻辑？最安全的说法是本介绍中的第一句话：模糊逻辑是一种将输入空间映射到输出空间的便捷方法。如果你发现它不方便，那就试试其他方法。如果已经存在更简单的解决方案，那就使用它。模糊逻辑是对常识的编纂–在实施时使用常识，你很可能会做出正确的决定。例如，许多控制器在不使用模糊逻辑的情况下也能做得很好。但是，如果您花时间熟悉模糊逻辑，就会发现它是一种非常强大的工具，可以快速有效地处理不精确和非线性问题。

1.4 模糊逻辑工具箱软件能做什么？

使用模糊逻辑工具箱软件，您可以

• 使用命令行功能或 Fuzzy Logic Designer 应用程序创建和编辑模糊推理系统。

• 使用聚类或自适应神经模糊技术自动生成模糊系统。

• 使用遗传算法和粒子群优化等优化方法自动调整模糊逻辑系统的参数。更多信息，请参阅调整模糊推理系统。

• 使用模糊逻辑控制器模块在 Simulink® 模型中模拟模糊系统。

• 自动生成评估模糊推理系统的代码。更多信息，请参阅部署模糊推理系统。

二、模糊逻辑学基础

2.1 概览

模糊逻辑的关键在于将输入空间映射到输出空间，而实现这一目标的主要机制是一系列被称为规则的 "如果-那么 "语句。所有规则都是并行评估的，规则的顺序并不重要。规则本身非常有用，因为它们指向变量和描述这些变量的形容词。在建立一个能解释规则的系统之前，您必须定义您计划使用的所有术语以及描述这些术语的形容词。如果说水是热的，就需要定义水温的预期变化范围以及热这个词的含义。

一般来说，模糊推理是一种解释输入向量中的值，并根据一组规则为输出向量赋值的方法。

本主题通过介绍模糊逻辑的理论和实践，引导您逐步完成模糊逻辑过程。

2.2 模糊集合

模糊逻辑始于模糊集的概念。模糊集是一个没有明确边界的集合。它可以包含只有部分成员度的元素。

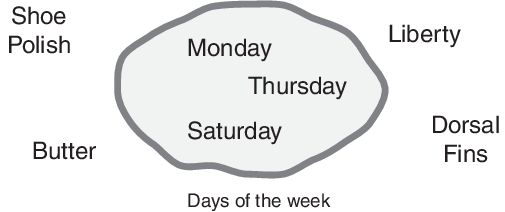
要理解什么是模糊集合，首先要考虑经典集合的定义。经典集合是一个完全包含或完全不包含任何给定元素的容器。例如，一周的天数集合无疑包括星期一、星期四和星期六。它同样毫无疑问地排除了黄油、自由和背鳍，等等。

这种集合被称为经典集合，因为它由来已久。亚里士多德首次提出了排除中间律，即 X 要么在集合 A 中，要么不在集合 A 中。这一定律的另一个版本是 在任何主题中，有一件事必须要么被肯定，要么被否定。

用注释重述这一定律： “在任何主题（比如说星期一）中，必须有一件事（一周中的一天）要么被断言，要么被否定（我断言星期一是一周中的一天）”。这一定律要求对立面，即 A 和非 A 这两个类别之间应该包含整个宇宙。万事万物不是属于其中一类，就是属于另一类。不存在既是星期又不是星期的事物。

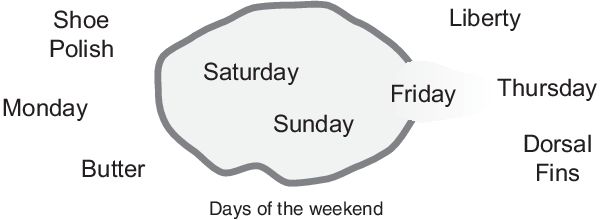
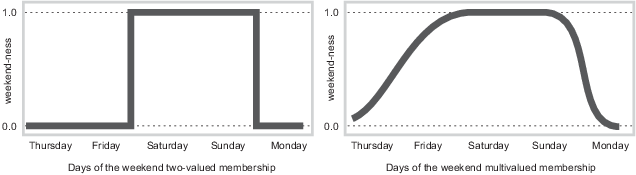
现在，我们来看看周末的天数集合。下图试图对周末天进行分类。

大多数人都认为周六和周日属于周末，那么周五呢？感觉上它是周末的一部分，但不知何故，从技术上讲，它似乎应该被排除在外。因此，周五 “横跨栅栏”。经典套装不能容忍这种分类。要么是在一个集合内，要么是在一个集合外。然而，人类的经验表明情况并非如此，"跨越栅栏 "是生活的一部分。

当然，在定义什么是周末时，必须考虑到个人的观念和文化背景。即使是字典也不精确，它把周末定义为从星期五晚上或星期六到星期一早上这段时间。你正在进入这样一个领域：尖锐的、"是 "与 "否 "的逻辑不再有用。模糊推理正是在你研究人们如何真正理解周末这个概念时才变得有价值，而不是仅仅为了会计目的而进行简单的分类。下面这句话为模糊逻辑奠定了基础。

在模糊逻辑中，任何陈述的真伪都取决于程度。

任何陈述都可以是模糊的。模糊推理的主要优势在于，它可以用一个 "不完全是 "或 "不是 "的答案来回答一个 "是 "或 "否 "的问题。人类经常做这样的事情（想想看，你很少能在一个看似简单的问题上得到一个直接的答案），但对于计算机来说，这是一个相当新的技巧。

它是如何工作的？模糊逻辑推理只是对我们熟悉的 "是 "与 “否”（布尔）逻辑进行了概括。如果给 "真 "取数值 1，给 "假 "取数值 0，那么这个数值表示模糊逻辑也允许取介于 0.2 和 0.7453 之间的数值。例如

问：星期六是周末吗？
答：1（是，或真实）
问：星期二是周末吗？
答：0（否，或假）
问：星期五是周末吗？
答：0.8（大部分是，但不完全是）
问：星期天是周末吗？
答：0.95（是，但不像周六那么多）。

左边的图显示了如果您被迫做出绝对 "是 "或 "否 "的回答，"周末性 "的真值。右边的图表显示了如果允许您用模糊的中间值来回答周末性的真值。

从技术上讲，右边的表示来自多值逻辑（或多价逻辑）领域。如果你问 “X 是集合 A 的成员吗？”，答案可能是 “是”、"否 "或介于两者之间的无数个中间值中的任何一个。因此，X 可能是 A 中的部分成员。多值逻辑与我们更熟悉的二值（或二价 "是 "与 “否”）逻辑形成了直接对比。

回到刚才的例子，现在我们来看看周末性的连续时间图，如下图所示。

通过使曲线图连续，你就定义了某一时刻属于周末的程度，而不是属于一整天的程度。在左边的图中，请注意，在周五午夜，当秒针划过 12 点时，周末性的真值从 0 不连续地跳到了 1。这是定义周末的一种方法，虽然对会计师来说可能有用，但它可能与你自己在现实世界中对周末性的体验并不相符。

右边的图显示了一条平滑变化的曲线，它说明了这样一个事实，即整个星期五，以及在很小程度上，星期四的部分时间，都具有周末性的特征，因此都应该属于周末时刻模糊集合中的部分成员。定义任意时刻周末性的曲线是一个将输入空间（一周的时间）映射到输出空间（周末性）的函数。具体来说，它被称为成员函数。有关更详细的讨论，请参阅 “成员函数”。

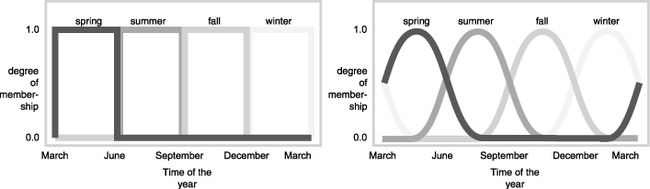
作为模糊集的另一个例子，请考虑季节问题。现在是什么季节？在北半球，夏季正式开始于地球轨道上北极最直接指向太阳的时刻。它每年正好出现一次，在 6 月下旬。根据天文学对季节的定义，我们可以得到如下图左侧所示的清晰界限。但是，如下图右侧所示（在北半球温带气候区），您所经历的季节或多或少会持续变化。

2.3 成员函数

会籍函数（MF）是一条曲线，它定义了输入空间中的每个点如何映射到介于 0 和 1 之间的会籍值（或会籍度）。

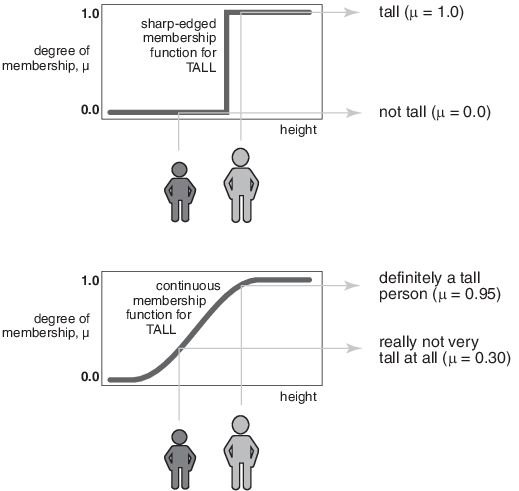
模糊集最常用的例子之一是高个子集合。在这种情况下，讨论范围是所有潜在的身高，比如从 3 英尺到 9 英尺。高个子一词对应于一条曲线，这条曲线定义了任何人的高个子程度。如果给 "高个子 "这个集合设定了一个经典集合的明确（清晰）边界，那么你就可以说，所有身高超过六英尺的人都被正式视为高个子。然而，当一个人和另一个人的身高只相差一英寸时，就把他们分别称为矮个子和高个子是不合理的。

如果前面显示的那种区分是行不通的，那么什么才是界定高个子人群的正确方法呢？与周末天数图一样，下图显示了一条从不高到高的平滑变化曲线。输出轴是一个介于 0 和 1 之间的数字，称为成员值。该曲线称为成员函数，通常用 µ 表示。在上图中，两个人被划分为完全高或完全不高。在下图中，平滑过渡允许不同程度的身高。两个人在某种程度上都很高，但其中一人的身高明显低于另一人。个子较高的人，其身高属性为 0.95，肯定是个高个子，但身高属性为 0.3 的人并不高。

模糊集合中包含了主观解释和适当的单位。如果你说 “她很高”，那么 "高 "的成员函数就应该考虑到你指的是一个六岁的孩子还是一个成年女性。同样，单位也包含在曲线中，因为说 "她的身高是英寸还是米？"是没有意义的。

2.4 模糊逻辑工具箱软件中的成员函数

成员函数必须满足的唯一条件是，其成员值必须在 0 和 1 之间变化。函数本身可以是任意优化的，以满足您对简单、方便、快速和高效的需求。

一个经典的集合可以表示为

$A=\{x|x>6\}$

模糊集合是经典集合的扩展。如果 X 是话语宇宙，其元素用 x 表示，那么 X 中的模糊集 A 定义为有序对的集合。

$A\{x,\mu A(x)|x\in X\}$

µA(x) 称为 x 在 A 中的成员资格函数（或 MF）。成员资格函数将 X 的每个元素映射为介于 0 和 1 之间的成员资格值。

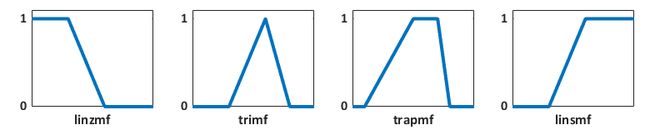
模糊逻辑工具箱™ 软件包含 13 种内置成员函数类型。这些函数又由几个基本函数构建而成。

• 分段线性函数

• 高斯分布函数

• 曲线

• 二次和三次多项式曲线

最简单的成员函数是用直线构成的。这些直线型成员资格函数具有简单的优点。

• trimf - 三角阶乘函数

• trapmf - 梯形会籍函数

• linzmf - 向左开口的直线 Z 型成员资格函数（自 R2022a 版起使用）

• linsmf - 向右开放的线性 s 型成员资格函数（自 R2022a 版起）

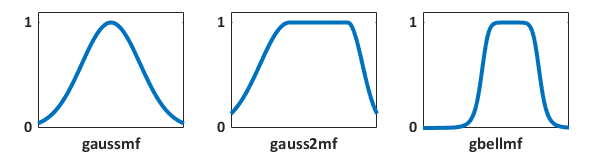
从高斯分布衍生出两种成员资格函数：简单高斯曲线（gaussmf）和不同高斯曲线的双面复合（gauss2mf）。

广义钟形成员函数（gbellmf）在 0 和 1 之间也有类似的平滑过渡。

高斯成员函数和钟形成员函数因其平滑性和简洁的符号而成为指定模糊集合的常用方法。这两种曲线的优点都是平滑且在所有点上都不为零。

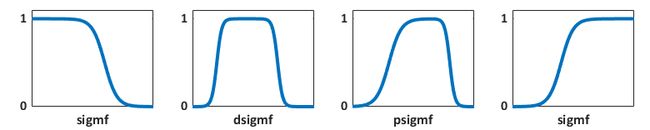
虽然高斯曲线和钟形曲线实现了平滑性，但它们无法指定非对称成员资格函数，而这在某些应用中非常重要。为此，你可以使用西格莫成员函数 (sigmf)，这是一种向左或向右开放的平滑成员函数。你可以根据两个西格玛函数的差值（dsigmf）或乘积（psigmf）创建非对称和封闭的成员函数。

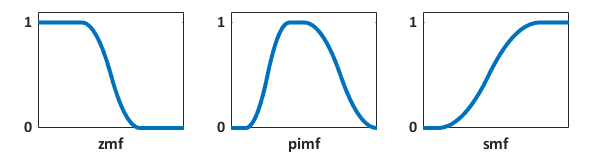
您还可以使用基于多项式的曲线创建平滑的成员资格函数，这些曲线因其形状而得名。

• zmf - 向左开放的 Z 型成员资格函数

• smf - 向右开放的 S 型成员资格函数

• pimf - Pi- 形会籍函数，它是 S 形和 Z 形会籍函数的乘积

你还可以创建自己的自定义成员函数。更多信息，请参阅使用自定义函数构建模糊系统。

2.5 逻辑运算

既然你已经理解了模糊推理，那么就需要看看模糊推理与逻辑运算是如何联系在一起的。

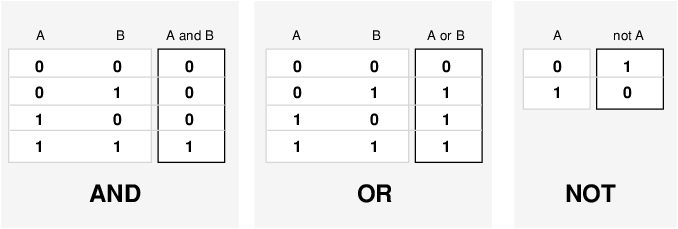
关于模糊逻辑推理，最重要的一点是，它是标准布尔逻辑的超集。换句话说，如果将模糊值保持在 1（全真）和 0（全假）这两个极端，标准逻辑运算就会成立。举例来说，请看下面的标准真值表。

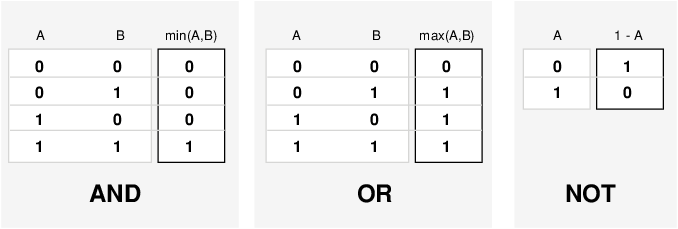
考虑到在模糊逻辑中，任何语句的真假都是一个程度问题，这些真值表是否可以改变？输入值可以是介于 0 和 1 之间的实数。什么函数既能保留 AND 真值表（例如）的结果，又能扩展到介于 0 和 1 之间的所有实数？

答案之一是最小运算。也就是说，使用函数 min(A,B) 来解析语句 A AND B，其中 A 和 B 的范围限定为 (0,1)。根据同样的推理，可以用 max 函数替换 OR 运算，这样 A OR B 就等价于 max(A,B)。最后，NOT A 运算等价于 1-A 运算。经过这样的替换，前面的真值表就完全不变了。

此外，由于真值表背后有一个函数，而不仅仅是真值表本身，因此现在可以考虑 1 和 0 以外的值。

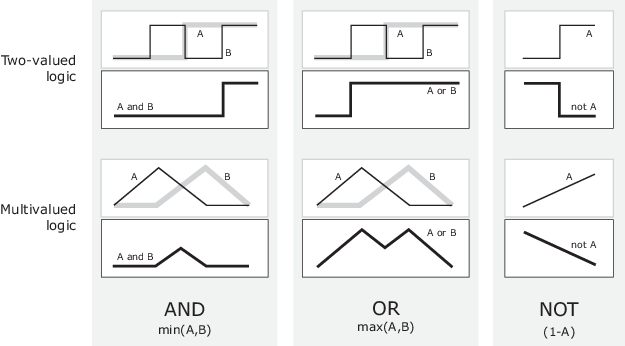
下图使用图形来显示相同的信息。在这幅图中，真值表被转换成了两个模糊集的图，两个模糊集一起应用创建了一个模糊集。图的上半部分显示的是与前面的两值真值表相对应的图，而图的下半部分显示的是如何根据您定义的模糊运算，在真值 A 和 B 的连续变化范围内进行运算。

有了这三个函数，就可以使用模糊集和模糊逻辑运算 AND、OR 和 NOT 来解决任何构造问题。

其他模糊运算符

在这种情况下，您只定义了 AND、OR 和 NOT 的二值逻辑运算与多值逻辑运算之间的一种特定对应关系。这种对应关系绝非唯一。

从更广义的角度来看，您定义的是模糊交集或连接（AND）、模糊联合或析取（OR）和模糊补码（NOT）。这些函数的经典运算符是 AND = 最小值，OR = 最大值，NOT = 加法补码。通常情况下，大多数模糊逻辑应用都会使用这些运算，并将其抛诸脑后。但一般来说，这些函数是任意的。如上图所示，模糊逻辑工具箱软件使用经典运算符进行模糊补码，但也可以自定义 AND 和 OR 运算符。

两个模糊集 A 和 B 的交集一般由二元映射 T 指定，它将两个成员函数聚合如下：

$\mu A\cap B(x)=T(\mu A(x),\mu B(x))$

例如，二元算子 T 可以表示 µA(x) 和 µB(x) 的乘法。这些模糊交集算子通常被称为 T-norm（三角规范）算子，符合以下基本要求：

T-norm 算子是二元映射 T(.,.)，具有以下属性：

边界 - T(0,0)=0, T(a,1)=T(1,a)=a

单调性 - 若 a≤c 且 b≤d 则 T(a,b)≤T(c,d)

交换性 - T(a,b)=T(b,a)

关联性–T(a,T(b,c))=T(T(a,b),c)

第一个要求是对干脆集的正确概括。第二个要求意味着，A 或 B 中成员值的减少不会导致 A 交叉点 B 中成员值的增加。最后，第四个要求允许我们以任意成对分组的顺序取任意数量集合的交集。

与模糊交集一样，模糊联合算子一般由二元映射 S 指定：

$\mu A\cup B(x)=S(\mu A(x),\mu B(x))$

例如，二元算子 S 可以表示 µA(x) 和 µB(x) 的加法。这些模糊联合算子通常被称为 T-conorm（或 S-norm）算子，它们必须满足以下基本要求：

T-conorm（或 S-norm）算子是二元映射 S(.,.)，具有以下属性：

边界 - S(1,1)=1, S(a,0)=S(0,a)=a

单调性 - 若 a≤c 且 b≤d 则 S(a,b)≤S(c,d)

交换性 - S(a,b)=S(b,a)

关联性 - S(a,S(b,c))=S(S(a,b),c)

过去曾提出过几种参数化 T 准则和对偶 T 准则，如 Yager [11]、Dubois 和 Prade [1]、Schweizer 和 Sklar [8] 以及 Sugeno [9]。它们都提供了一种改变函数增益的方法，使其可以非常严格或非常宽松。

2.6 If-Then 规则

模糊集和模糊运算符是模糊逻辑的主语和动词。这些 "如果-那么 "规则语句用于制定构成模糊逻辑的条件语句。

单个模糊 "如果-那么 "规则的形式为

如果 x 是 A，那么 y 就是 B

其中，A 和 B 分别是模糊集在 X 和 Y 范围（话语宇宙）上定义的语言值。规则中 "x 是 A "的 if 部分称为前件或前提，而规则中 "y 是 B "的 then 部分称为后果或结论。这样一条规则的例子可能是

如果服务很好，那么小费就是一般水平

相反，平均值表示为一个模糊集，因此结果是将整个模糊集 B 赋值给输出变量 y 的赋值。在 if-then 规则中，单词 is 有两种完全不同的用法，这取决于它是出现在前因后果中。用 MATLAB® 术语来说，这种用法就是使用"==“的关系测试和使用”="符号的变量赋值之间的区别。较少混淆的规则写法是

如果服务 == 好，那么小费 = 平均值

一般来说，if-then 规则的输入是输入变量（本例中为服务）的当前值，输出是整个模糊集（本例中为平均值）。这个集合稍后将被去模糊化，为输出赋予一个值。下一节将介绍去模糊化的概念。

解释 "如果-那么 "规则涉及两个步骤：

评估前件 - 对输入进行模糊化并应用必要的模糊运算符。

将结果应用于结果。

第二步称为蕴涵。在二元逻辑中，如果 p 为真，那么 q 也为真（p → q）。在模糊逻辑中，如果 p 在一定程度上为真，那么 q 也在相同程度上为真（0.5p → 0.5q）。在这两种情况下，如果 p 为假，那么 q 的值是不确定的。

规则的前件可以有多个部分。

如果天空灰蒙蒙的，风很大，气压在下降，那么 …

在这种情况下，前件的所有部分都同时计算，并使用上一节所述的逻辑运算符解析为一个数字。规则的结果也可以有多个部分。

如果温度较低，则热水阀打开，冷水阀关闭

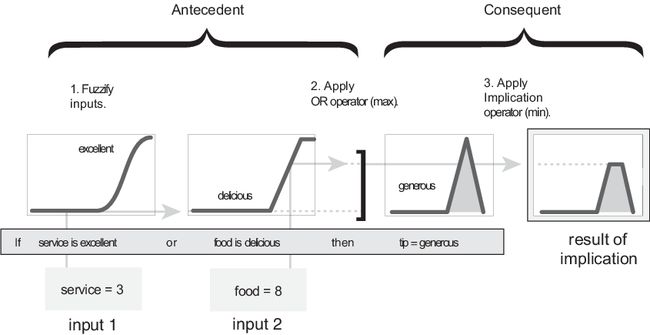
在这种情况下，所有后件都同样受到前件结果的影响。结果如何受到前件的影响？后件指定了一个模糊集分配给输出。然后，蕴涵函数按照前件指定的程度修改该模糊集。修改输出模糊集的最常用方法是使用 min 函数截断（如下图所示，模糊集被截断）或使用 prod 函数缩放（输出模糊集被缩小）。工具箱支持这两种方法，但在本节的示例中使用的是截断方法。

如果-那么规则摘要
解释 "如果-那么 "规则由三部分组成。下一节将详细解释这一过程：

模糊化输入： 如果前件只有一个部分，那么这就是规则的支持度。

对多部分前件应用模糊运算符： 如果前件有多个部分，则应用模糊逻辑运算符，将前件解析为介于 0 和 1 之间的一个数字，这就是规则的支持度。

应用蕴涵法： 使用整个规则的支持度来形成输出模糊集。模糊规则的结果将整个模糊集分配给输出。这个模糊集由一个成员函数表示，该成员函数的选择是为了表明结果的质量。如果前件仅部分为真（即赋值小于 1），那么输出模糊集将根据蕴含法进行截断。

一般来说，单靠一条规则是无效的。需要两个或更多可以相互影响的规则。每条规则的输出都是一个模糊集。然后将每条规则的输出模糊集汇总为一个输出模糊集。最后，生成的集合会被去模糊化，或解析为一个数字。使用模糊逻辑设计器构建模糊系统》展示了一种特殊类型的模糊推理系统（称为马姆达尼型）从开始到结束的整个工作过程。

三、模糊推理过程

模糊推理是利用模糊逻辑制定从给定输入到输出的映射过程。然后，映射提供了一个基础，据此可以做出决策或判别模式。模糊推理过程涉及成员函数、逻辑运算和 "如果-那么 "规则中描述的所有部分。

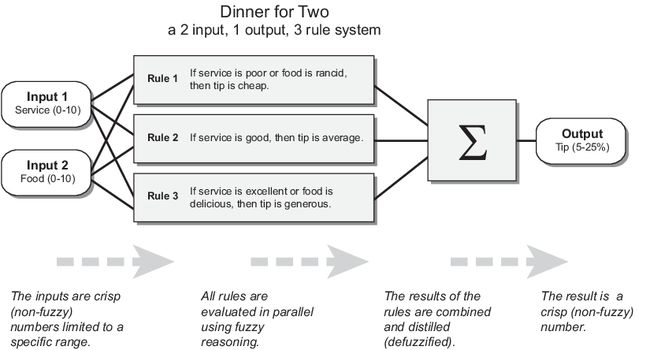
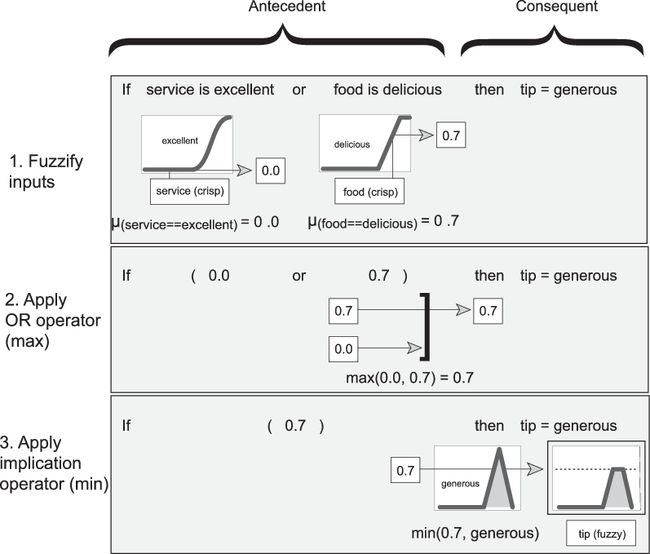
本节介绍模糊推理过程，并以《模糊与非模糊逻辑》中的两输入一输出三规则小费问题为例。该问题的模糊推理系统将服务和食物质量作为输入，并使用以下规则计算小费百分比。

1. 如果服务差或食物变质，则小费便宜。

2. 如果服务良好，则小费一般。

3. 如果服务出色或食物美味，则小费丰厚。

规则的并行性是模糊逻辑系统的一个重要方面。逻辑不是根据断点在不同模式间急剧切换，而是从一个或另一个规则占主导地位的区域流畅地流动。

模糊推理过程包括以下步骤。

• 输入变量的模糊化

• 在前项中应用模糊运算符（AND 或 OR

• 从前件到后件的暗示

• 将结果汇总到各规则中

• 去模糊化

3.1 对输入进行模糊化处理

第一步是获取输入，并通过成员函数（模糊化）确定它们属于每个相应模糊集的程度。在模糊逻辑工具箱（Fuzzy Logic Toolbox™）软件中，输入始终是一个清晰的数值，仅限于输入变量的话语范围（本例中为 0 到 10 的区间）。输出则是限定语言集合中的模糊成员度（区间总是从 0 到 1）。输入的模糊化相当于表格查找或函数评估。

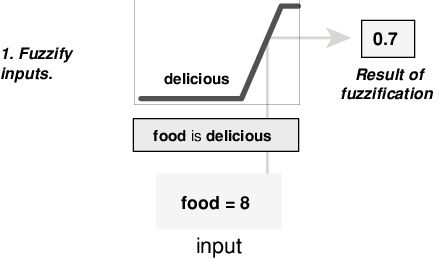
本例基于三条规则，每条规则都取决于将输入解析为几个不同的模糊语言集：服务差、服务好、食物馊、食物可口，等等。在对规则进行评估之前，必须根据每个语言集对输入进行模糊化。例如，食物的美味程度如何？下图显示了假设餐厅的食物（按 0 到 10 的评分标准评分）在语言变量 "美味 "中的合格程度。在本例中，我们将食物评为 8 分，根据美味的图形定义，美味成员函数的µ = 0.7。

通过这种方式，每个输入都会在规则要求的所有合格成员函数上进行模糊化。

3.2 应用模糊运算符

在对输入进行模糊化处理后，就可以知道每条规则的先决条件各部分的满足程度。如果一条规则的前项有多个部分，则应用模糊运算符获得一个数字，代表规则前项的结果。然后将该数字应用于输出函数。模糊运算器的输入是来自模糊化输入变量的两个或多个成员值。输出则是一个单一的真值。

正如逻辑运算中所描述的，任何定义明确的方法都可以代替 AND 运算或 OR 运算。工具箱支持两种内置 AND 运算方法：min（最小值）和 prod（乘积）。此外，还支持两种内置 OR 方法：max（最大）和 probor（概率 OR）。概率 OR 方法（也称为代数和）的计算公式为

probor(a,b) = a + b - ab

除了这些内置方法外，您还可以通过编写任意函数并将其设置为您选择的方法，来创建自己的 AND 和 OR 方法。更多信息，请参阅使用自定义函数构建模糊系统。

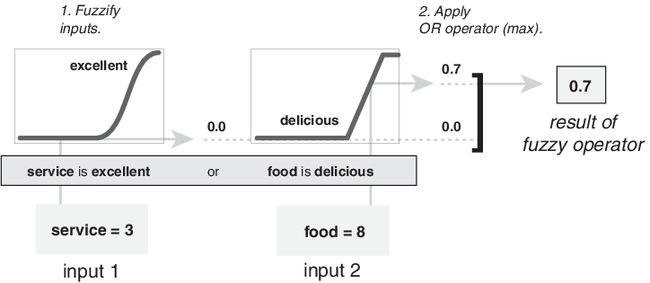
下图通过评估小费计算的第三条规则的前项演示了 OR 运算符 max。对于给定的服务和食物评分，前因的两个元素（服务极好和食物美味）分别产生模糊成员值 0.0 和 0.7。模糊 OR 运算符选择两个值中的最大值 0.7。概率 OR 方法的结果仍然是 0.7。

应用蕴含法

在应用蕴涵法之前，必须确定规则权重。每条规则都有一个权重（一个从 0 到 1 的数字），它被应用于前件所给出的数字。一般情况下，权重为 1（如本例所示），因此对蕴涵过程没有影响。但是，您可以通过将某条规则的权重值改为 1 以外的值来降低它相对于其他规则的影响。

在为每条规则分配了适当的权重后，蕴涵方法就开始实施了。结果是一个由成员函数表示的模糊集合，成员函数对归属于它的语言特点进行适当加权。使用与前件（单个数字）相关的函数对后件进行重塑。蕴涵过程的输入是前件给出的单个数字，输出是一个模糊集。蕴涵是针对每条规则实现的。支持两种内置方法，它们与 AND 方法使用的函数相同：min（最小值）和 prod（乘积），前者用于截断输出模糊集，后者用于缩放输出模糊集。

---