C#代码-摄影测量实习-解析空中三角测量

大三学期中的摄影测量实习
以下是C#窗体代码-以供同学们学习 (
相较于其他方法，解析空三的代码略微繁琐，一般有1000多行

数据来源原文链接：https://blog.csdn.net/sheyun1876/article/details/80581910
注意 ：像对2中703、702的顺序问题需要读者自行考虑

1、  基本数据

摄影机主距：f＝153.033mm  bx＝200mm

2、  像对坐标数据（单位：微米）

像对1：    701         702   
======================================================== 
    1201      648790      735260     -230980      788550  
    1818      113860      595800     -771380      679190
    1202      241050      586260     -644640      661950
    1204      578030      223960     -327700      277590
    1203      256140      187820     -648360      260160
    1205      606230     -104550     -315660      -51440
    1206      278340     -565020     -660020     -487200
    1052      179220     -757800     -765430     -670400
     410      478510     -637940     -466930     -569840
     399      975930     -700850       16690     -658940
     192      917380      -16160       -4600       18540
     370      803150      758570      -76440      802960
    1118       94870      709670     -785850      795830
     194       35030      -34550     -877140       50930
    -398       19790     -843710     -925660     -745370

像对2：     703         702    
========================================================
     400     -568240     -631500      426790     -634450
    1207     -601170      642970      323920      637060
     399     -980300     -630600       16690     -658940
     192     -963100       51030       -4600       18540
     370     -989450      836700      -76410      802880
    1209       -8790      641530      921460      679700
     401      -29060     -915900      981740     -884160
    -190        1460        5490      965780       38900

像对3：    703         704    
========================================================
    1826      931930      729560      -26020      680090
     402      907100     -785750       20330     -836630
    1055      753660     -838360     -134160     -896670
     411      397770     -725220     -500070     -791380
    1211       49010       50160     -875490      -17320
     188      918060       48330      -10150       11950
    1225      890340      544420      -58540      499270
    1210      624000      444520     -317940      392160
    1209       -8690      641540     -945780      560530
     401      -29020     -915940     -930070    -1004070
    -190        1460        5460     -921980      -63410

3、控制点数据

点号        X坐标          Y坐标            Z坐标
==================================================
 1201      24204.689      46604.652         46.251
 1205      24343.683      45111.263         48.198
 1206      24965.047      44309.253         49.340
 1209      22167.904      46432.515         46.457

4、检查点数据

点号        X坐标          Y坐标          Z坐标
==================================================
 1118      25192.533      46608.059         48.936 
 1202      24941.046      46375.998         46.539
 1203      24945.705      45662.638         49.052
 1204      24369.486      45700.421         49.020
 1207      23218.292      46347.142         48.993

以下是Form1.cs程序：

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Analytic_aerial_triangulation
{
    public partial class Form1 : Form
    { 
        //基本数据
        double f = 0.153033;
        double bx = 0.2;
        //矩阵计算模块已被我封装，名称为MatrixOperations.cs
        MatrixOperations myMatrix = new MatrixOperations();
        

        public Form1()
        {
            InitializeComponent();
            
        }


        void ReadData(int i)
        {//数据读取函数
            OpenFileDialog myOpenFileDialog = new OpenFileDialog();      
            myOpenFileDialog.Title = "打开txt文件对话框";
            myOpenFileDialog.Filter = "txt文件|*.txt|所有文件|*.*";
            if (myOpenFileDialog.ShowDialog() == DialogResult.OK)
            {
                switch (i)
                {
                    case 1:
                        richTextBox1.LoadFile(myOpenFileDialog.FileName, RichTextBoxStreamType.PlainText);
                        break;
                    case 2:
                        richTextBox2.LoadFile(myOpenFileDialog.FileName, RichTextBoxStreamType.PlainText);
                        break;
                    case 3:
                        richTextBox3.LoadFile(myOpenFileDialog.FileName, RichTextBoxStreamType.PlainText);
                        break;
                }
            }
        }
       
        private void button1_Click(object sender, EventArgs e)
        {//像对坐标数据存储
            ReadData(1);
        }

        private void button2_Click(object sender, EventArgs e)
        {//控制点数据存储
            ReadData(2);
        }

        private void button3_Click(object sender, EventArgs e)
        {//检查点数据存储
            ReadData(3);
        }

        private void button4_Click(object sender, EventArgs e)
        {
            //先进行数据的初始化
            //点号
            double[] points1_Name = new double[15];
            double[] points2_Name = new double[8];
            double[] points3_Name = new double[11];
            //像点坐标
            double[] left1_x = new double[15]; double[] right1_x = new double[15];
            double[] left1_y = new double[15]; double[] right1_y = new double[15];
            double[] left2_x = new double[8]; double[] right2_x = new double[8];
            double[] left2_y = new double[8]; double[] right2_y = new double[8];
            double[] left3_x = new double[11]; double[] right3_x = new double[11];
            double[] left3_y = new double[11]; double[] right3_y = new double[11];
            //投影系数
            double[] N1_1 = new double[15]; double[] N1_2 = new double[15];
            double[] N2_1 = new double[8]; double[] N2_2 = new double[8];
            double[] N3_1 = new double[11]; double[] N3_2 = new double[11];
            //摄影基线分量
            double[] bx = new double[3];
            double[] by = new double[3];
            double[] bz = new double[3];
            //像空间辅助坐标系-像点
            double[] LeftPoint1_fz_x = new double[15];
            double[] LeftPoint1_fz_y = new double[15];
            double[] LeftPoint1_fz_z = new double[15];

            double[] LeftPoint2_fz_x = new double[8];
            double[] LeftPoint2_fz_y = new double[8];
            double[] LeftPoint2_fz_z = new double[8];

            double[] LeftPoint3_fz_x = new double[11];
            double[] LeftPoint3_fz_y = new double[11];
            double[] LeftPoint3_fz_z = new double[11];

            double[] RightPoint1_fz_y = new double[15];
            double[] RightPoint2_fz_y = new double[8];
            double[] RightPoint3_fz_y = new double[11];
            //像空间辅助坐标系-模型点
            double[] ModelPoint_1_x = new double[15];
            double[] ModelPoint_1_y = new double[15];
            double[] ModelPoint_1_z = new double[15];

            double[] ModelPoint_2_x = new double[8];
            double[] ModelPoint_2_y = new double[8];
            double[] ModelPoint_2_z = new double[8];

            double[] ModelPoint_3_x = new double[11];
            double[] ModelPoint_3_y = new double[11];
            double[] ModelPoint_3_z = new double[11];

            //像对坐标数据读取
            string[] line = richTextBox1.Text.Split('\n');
            for (int i = 0; i < 15; i++)
            {
                string[] PointData1 = line[i].Split(' ');
                points1_Name[i] = Convert.ToDouble(PointData1[0]);
                left1_x[i] = Convert.ToDouble(PointData1[1]) / 1000000.0;
                left1_y[i] = Convert.ToDouble(PointData1[2]) / 1000000.0;
                right1_x[i] = Convert.ToDouble(PointData1[3]) / 1000000.0;
                right1_y[i] = Convert.ToDouble(PointData1[4]) / 1000000.0;
            }
            for (int i = 15; i < 23; i++)
            {
                string[] PointData2 = line[i].Split(' ');
                points2_Name[i - 15] = Convert.ToDouble(PointData2[0]);
                left2_x[i - 15] = Convert.ToDouble(PointData2[1]) / 1000000.0;
                left2_y[i - 15] = Convert.ToDouble(PointData2[2]) / 1000000.0;
                right2_x[i - 15] = Convert.ToDouble(PointData2[3]) / 1000000.0;
                right2_y[i - 15] = Convert.ToDouble(PointData2[4]) / 1000000.0;
            }
            for (int i = 23; i < 34; i++)
            {
                string[] PointData3 = line[i].Split(' ');
                points3_Name[i - 23] = Convert.ToDouble(PointData3[0]);
                left3_x[i - 23] = Convert.ToDouble(PointData3[1]) / 1000000.0;
                left3_y[i - 23] = Convert.ToDouble(PointData3[2]) / 1000000.0;
                right3_x[i - 23] = Convert.ToDouble(PointData3[3]) / 1000000.0;
                right3_y[i - 23] = Convert.ToDouble(PointData3[4]) / 1000000.0;
            }

            double[,] roElements1 = new double[5, 1];
            double[,] roElements2 = new double[5, 1];
            double[,] roElements3 = new double[5, 1];
            double[,] roElements_gaizheng = new double[15,1];
            //确定相对定向元素的初始值
            for (int i = 0; i < 5; i++)
            {
                roElements1[i, 0] = 0;
            }
            XDDX(15, left1_x, left1_y, right1_x, right1_y,roElements_gaizheng ,roElements1, ModelPoint_1_x, ModelPoint_1_y, ModelPoint_1_z, N1_1, N1_2, LeftPoint1_fz_x, LeftPoint1_fz_y, LeftPoint1_fz_z,RightPoint1_fz_y, ref bx[0], ref by[0], ref bz[0]);
            for (int i = 0; i < 5; i++)
            {
                roElements2[i, 0] = roElements1[i, 0];
            }
            XDDX(8, left2_x, left2_y, right2_x, right2_y, roElements_gaizheng, roElements2, ModelPoint_2_x, ModelPoint_2_y, ModelPoint_2_z, N2_1, N2_2, LeftPoint2_fz_x, LeftPoint2_fz_y, LeftPoint2_fz_z, RightPoint2_fz_y, ref bx[1], ref by[1], ref bz[1]);
            for (int i = 0; i < 5; i++)
            {
                roElements3[i, 0] = roElements2[i, 0];
            }
            XDDX(11, left3_x, left3_y, right3_x, right3_y, roElements_gaizheng, roElements3, ModelPoint_3_x, ModelPoint_3_y, ModelPoint_3_z, N3_1, N3_2, LeftPoint3_fz_x, LeftPoint3_fz_y, LeftPoint3_fz_z, RightPoint3_fz_y, ref bx[2], ref by[2], ref bz[2]);

            //比例尺归化系数
            double[] k = new double[3];
            k[0] = 1;

            double[] k1 = new double[3];

            //找三个公共点点进行计算
            k1[0] = (N1_1[9] * LeftPoint1_fz_z[9] - bz[0]) / (N2_1[2] * LeftPoint2_fz_z[2]);
            k1[1] = (N1_1[10] * LeftPoint1_fz_z[10] - bz[0]) / (N2_1[3] * LeftPoint2_fz_z[3]);
            k1[2] = (N1_1[11] * LeftPoint1_fz_z[11] - bz[0]) / (N2_1[4] * LeftPoint2_fz_z[4]);
            k[1] = (k1[0] + k1[1] + k1[2]) / 3.0;  

            double[] k2 = new double[3];
            k2[0] = (N2_1[5] * LeftPoint2_fz_z[5] - bz[1]) / (N3_1[8] * LeftPoint3_fz_z[8]);
            k2[1] = (N2_1[6] * LeftPoint2_fz_z[6] - bz[1]) / (N3_1[9] * LeftPoint3_fz_z[9]);
            k2[2] = (N2_1[7] * LeftPoint2_fz_z[7] - bz[1]) / (N3_1[10] * LeftPoint3_fz_z[10]);
            k[2] = ((k2[0] + k2[1] + k2[2]) / 3.0) * k[1];    
           
            //控制点与像片点计算比例尺
            //定义地面控制点
            double[] XControl = new double[4];
            double[] YControl = new double[4];
            double[] ZControl = new double[4];
            //读取控制点坐标
            string[] lines = richTextBox2.Text.Split('\n');
            for (int i = 0; i < lines.Length; i++)
            {
                string[] Data = lines[i].Split(' ');
                XControl[i] = Convert.ToDouble(Data[1]);
                YControl[i] = Convert.ToDouble(Data[2]);
                ZControl[i] = Convert.ToDouble(Data[3]);
            }

            //通过三个点互相之间的距离来计算比例尺
            double m1, m2, m3;
            m1 = (Math.Sqrt((XControl[0] - XControl[1]) * (XControl[0] - XControl[1]) + (YControl[0] - YControl[1]) * (YControl[0] - YControl[1])))
                / (Math.Sqrt((left1_x[0] - left1_x[5]) * (left1_x[0] - left1_x[5]) + (left1_y[0] - left1_y[5]) * (left1_y[0] - left1_y[5])));
            m2 = (Math.Sqrt((XControl[0] - XControl[2]) * (XControl[0] - XControl[2]) + (YControl[0] - YControl[2]) * (YControl[0] - YControl[2])))
                / (Math.Sqrt((left1_x[0] - left1_x[6]) * (left1_x[0] - left1_x[6]) + (left1_y[0] - left1_y[6]) * (left1_y[0] - left1_y[6])));
            m3 = (Math.Sqrt((XControl[2] - XControl[1]) * (XControl[2] - XControl[1]) + (YControl[2] - YControl[1]) * (YControl[2] - YControl[1])))
                / (Math.Sqrt((left1_x[6] - left1_x[5]) * (left1_x[6] - left1_x[5]) + (left1_y[6] - left1_y[5]) * (left1_y[6] - left1_y[5])));         
            double avg_m = (m1 + m2 + m3) / 3.0;


            //摄站的摄影测量坐标
            //求出摄站点坐标之后用于下面求模型点摄影测量坐标系坐标
            double[] Xs_sheyingceliang = new double[4];
            double[] Ys_sheyingceliang = new double[4];
            double[] Zs_sheyingceliang = new double[4];
            for (int i = 0; i < 4; i++)  
            {//四个摄站
                if (i == 0) 
                {
                    Xs_sheyingceliang[0] = 0.0;
                    Ys_sheyingceliang[0] = 0.0;
                    Zs_sheyingceliang[0] = avg_m * f;
                }
                else  
                {
                    Xs_sheyingceliang[i] = Xs_sheyingceliang[i - 1] + avg_m * k[i - 1] * bx[i - 1];
                    Ys_sheyingceliang[i] = Ys_sheyingceliang[i - 1] + avg_m * k[i - 1] * by[i - 1];
                    Zs_sheyingceliang[i] = Zs_sheyingceliang[i - 1] + avg_m * k[i - 1] * bz[i - 1];
                }
            }
          

            //模型点摄影测量坐标
            double[,] model_sheyingceliang_first = new double[15, 3];
            double[,] model_sheyingceliang_second = new double[8, 3];
            double[,] model_sheyingceliang_third = new double[11, 3];

            //模型点摄测坐标计算
            
            for (int i = 0; i < 15; i++)
            {//像对1
                model_sheyingceliang_first[i, 0] = Xs_sheyingceliang[0] + k[0] * avg_m * N1_1[i] * LeftPoint1_fz_x[i];
                model_sheyingceliang_first[i, 1] = 0.5 * (Ys_sheyingceliang[0] + k[0] * avg_m * N1_1[i] * LeftPoint1_fz_y[i] + Ys_sheyingceliang[1] + k[0] * avg_m * N1_2[i] * RightPoint1_fz_y[i]);
                model_sheyingceliang_first[i, 2] = Zs_sheyingceliang[0] + k[0] * avg_m * N1_1[i] * LeftPoint1_fz_z[i];
            }
            for (int i = 0; i < 8; i++)
            {
                model_sheyingceliang_second[i, 0] = Xs_sheyingceliang[1] + k[1] * avg_m * N2_1[i] * LeftPoint2_fz_x[i];
                model_sheyingceliang_second[i, 1] = 0.5 * (Ys_sheyingceliang[1] + k[1] * avg_m * N2_1[i] * LeftPoint2_fz_y[i] + Ys_sheyingceliang[2] + k[1] * avg_m * N2_2[i] * RightPoint2_fz_y[i]);
                model_sheyingceliang_second[i, 2] = Zs_sheyingceliang[1] + k[1] * avg_m * N2_1[i] * LeftPoint2_fz_z[i];
            }
            for (int i = 0; i < 11; i++)
            {
                model_sheyingceliang_third[i, 0] = Xs_sheyingceliang[2] + k[2] * avg_m * N3_1[i] * LeftPoint3_fz_x[i];
                model_sheyingceliang_third[i, 1] = 0.5 * (Ys_sheyingceliang[2] + k[2] * avg_m * N3_1[i] * LeftPoint3_fz_y[i] + Ys_sheyingceliang[3] + k[2] * avg_m * N3_2[i] * RightPoint3_fz_y[i]);
                model_sheyingceliang_third[i, 2] = Zs_sheyingceliang[2] + k[2] * avg_m * N3_1[i] * LeftPoint3_fz_z[i];
            }



            //控制点地面摄影测量坐标
            double[] control_dimianshece_x = new double[4];
            double[] control_dimianshece_y = new double[4];
            double[] control_dimianshece_z = new double[4];

            //模型点摄影测量坐标
            double[] modelX = new double[4];
            double[] modelY = new double[4];
            double[] modelZ = new double[4];

            //绝对定向元素
            double delta_x, delta_y, delta_z, lamda, fai, omiga, kappa;

            //绝对定向过程
            //先根据公式存下坐标变换差
            //大地坐标差
            double delta_Xt = 0;
            double delta_Yt = 0;
            //摄影测量坐标差
            double delta_Xp = 0;
            double delta_Yp = 0;
            //转换参数和缩放系数
            double a, b, lamda1;

            //利用求转换参数和缩放系数
            delta_Xt = XControl[0] - XControl[3]; //第一个和最后一个控制点
            delta_Yt = YControl[0] - YControl[3];

            //从模型点的摄影测量坐标入手
            delta_Xp = model_sheyingceliang_first[0, 0] - model_sheyingceliang_third[8, 0];  //第一个像对的第一个模型点和最后一个像对的最后一个模型点
            delta_Yp = model_sheyingceliang_first[0, 1] - model_sheyingceliang_third[8, 1];

            a = (delta_Xp * delta_Yt + delta_Yp * delta_Xt) / (delta_Xt * delta_Xt + delta_Yt * delta_Yt);
            b = (delta_Xp * delta_Xt - delta_Yp * delta_Yt) / (delta_Xt * delta_Xt + delta_Yt * delta_Yt);
            lamda1 = Math.Sqrt(a * a + b * b);

            //四组模型点的摄影测量坐标系坐标，用来计算绝对定向元素
            //根据模型点的点号去找到算出来的点的对应的摄影测量坐标
            modelX[0] = model_sheyingceliang_first[0, 0];
            modelY[0] = model_sheyingceliang_first[0, 1];
            modelZ[0] = model_sheyingceliang_first[0, 2];

            modelX[1] = model_sheyingceliang_first[5, 0];
            modelY[1] = model_sheyingceliang_first[5, 1];
            modelZ[1] = model_sheyingceliang_first[5, 2];

            modelX[2] = model_sheyingceliang_first[6, 0];
            modelY[2] = model_sheyingceliang_first[6, 1];
            modelZ[2] = model_sheyingceliang_first[6, 2];

            modelX[3] = model_sheyingceliang_third[8, 0];
            modelY[3] = model_sheyingceliang_third[8, 1];
            modelZ[3] = model_sheyingceliang_third[8, 2];

            //控制点大地坐标转换为地面摄影测量坐标
            for (int i = 0; i < 4; i++)
            {
                control_dimianshece_x[i] = b * (XControl[i] - XControl[0]) + a * (YControl[i] - YControl[0]);
                control_dimianshece_y[i] = a * (XControl[i] - XControl[0]) - b * (YControl[i] - YControl[0]);
                control_dimianshece_z[i] = lamda1 * (ZControl[i] - ZControl[0]);
            }

            //求解绝对定向元素
            double[,] B = new double[12, 7];//系数阵B
            double[,] R = new double[3, 3];//旋转矩阵R
            double[,] L = new double[12, 1];//常数项L
            double[,] dx = new double[7, 1];//改正数dx  

            //确定绝对定向元素的初始值
            delta_x = 0;
            delta_y = 0;
            delta_z = 0;
            lamda = 1;
            fai = 0;
            omiga = 0;
            kappa = 0;

            //计算系数矩阵B
            for (int i = 0; i < 4; i++)
            {
                B[3 * i, 0] = 1;
                B[3 * i, 1] = 0;
                B[3 * i, 2] = 0;
                B[3 * i, 3] = modelX[i];
                B[3 * i, 4] = -modelZ[i];
                B[3 * i, 5] = 0;
                B[3 * i, 6] = -modelY[i];

                B[3 * i + 1, 0] = 0;
                B[3 * i + 1, 1] = 1;
                B[3 * i + 1, 2] = 0;
                B[3 * i + 1, 3] = modelY[i];
                B[3 * i + 1, 4] = 0;
                B[3 * i + 1, 5] = -modelZ[i];
                B[3 * i + 1, 6] = modelX[i];

                B[3 * i + 2, 0] = 0;
                B[3 * i + 2, 1] = 0;
                B[3 * i + 2, 2] = 1;
                B[3 * i + 2, 3] = modelZ[i];
                B[3 * i + 2, 4] = modelX[i];
                B[3 * i + 2, 5] = modelY[i];
                B[3 * i + 2, 6] = 0;
            }

            int count = 0;

            for (int j = 0; ; j++)
            {
                //计算旋转矩阵R
                R[0, 0] = Math.Cos(fai) * Math.Cos(kappa) - Math.Sin(fai) * Math.Sin(omiga) * Math.Sin(kappa);
                R[0, 1] = -Math.Cos(fai) * Math.Sin(kappa) - Math.Sin(fai) * Math.Sin(omiga) * Math.Cos(kappa);
                R[0, 2] = -Math.Sin(fai) * Math.Cos(omiga);
                R[1, 0] = Math.Cos(omiga) * Math.Sin(kappa);
                R[1, 1] = Math.Cos(omiga) * Math.Cos(kappa);
                R[1, 2] = -Math.Sin(omiga);
                R[2, 0] = Math.Sin(fai) * Math.Cos(kappa) + Math.Cos(fai) * Math.Sin(omiga) * Math.Sin(kappa);
                R[2, 1] = -Math.Sin(fai) * Math.Sin(kappa) + Math.Cos(fai) * Math.Sin(omiga) * Math.Cos(kappa);
                R[2, 2] = Math.Cos(fai) * Math.Cos(omiga);
                //计算常数项L
                for (int i = 0; i < 4; i++)
                {
                    L[3 * i, 0] = control_dimianshece_x[i] - lamda * (modelX[i] - kappa * modelY[i] - fai * modelZ[i]) - delta_x;
                    L[3 * i + 1, 0] = control_dimianshece_y[i] - lamda * (kappa * modelX[i] + modelY[i] - omiga * modelZ[i]) - delta_y;
                    L[3 * i + 2, 0] = control_dimianshece_z[i] - lamda * (fai * modelX[i] + omiga * modelY[i] + modelZ[i]) - delta_z;
                }

                //计算改正数

                double[,] BT = new double[7, 12];//系数阵B的转置
                BT = myMatrix.Matrix_Transpose(B);
                double[,] BTB = new double[7, 7]; //BT*B
                BTB = myMatrix.Matrix_Multiply(BT, B);
                double[,] BTBN = new double[7, 7]; //BT*B的逆矩阵
                BTBN = myMatrix.Matrix_Reverse(BTB);
                double[,] BTBNBT = new double[7, 12]; //BT*B的逆矩阵乘B的转置
                BTBNBT = myMatrix.Matrix_Multiply(BTBN, BT);

                dx = myMatrix.Matrix_Multiply(BTBNBT, L);

                //将改正数赋给原来的初始值，得到下一次绝对定向元素的初始值
                delta_x += dx[0, 0];
                delta_y += dx[1, 0];
                delta_z += dx[2, 0];
                lamda += dx[3, 0];
                fai += dx[4, 0];
                omiga += dx[5, 0];
                kappa += dx[6, 0];

                //限制迭代100次
                if (count >= 100)
                {
                    break;
                }
                count = count + 1;
            }

           
            //计算出来的三个模型中的模型点地面摄影测量坐标
            double[,] modelpt1 = new double[15, 3];
            double[,] modelpt2 = new double[8, 3];
            double[,] modelpt3 = new double[11, 3];

            //计算模型点地摄测系的坐标
            for (int i = 0; i < 15; i++)
            {
                modelpt1[i, 0] = lamda * (model_sheyingceliang_first[i, 0] - kappa * model_sheyingceliang_first[i, 1] - fai * model_sheyingceliang_first[i, 2]) + delta_x;
                modelpt1[i, 1] = lamda * (kappa * model_sheyingceliang_first[i, 0] + model_sheyingceliang_first[i, 1] - omiga * model_sheyingceliang_first[i, 2]) + delta_y;
                modelpt1[i, 2] = lamda * (fai * model_sheyingceliang_first[i, 0] + omiga * model_sheyingceliang_first[i, 1] + model_sheyingceliang_first[i, 2]) + delta_z;
            }
            for (int i = 0; i < 8; i++)
            {
                modelpt2[i, 0] = lamda * (model_sheyingceliang_second[i, 0] - kappa * model_sheyingceliang_second[i, 1] - fai * model_sheyingceliang_second[i, 2]) + delta_x;
                modelpt2[i, 1] = lamda * (kappa * model_sheyingceliang_second[i, 0] + model_sheyingceliang_second[i, 1] - omiga * model_sheyingceliang_second[i, 2]) + delta_y;
                modelpt2[i, 2] = lamda * (fai * model_sheyingceliang_second[i, 0] + omiga * model_sheyingceliang_second[i, 1] + model_sheyingceliang_second[i, 2]) + delta_z;
            }
            for (int i = 0; i < 11; i++)
            {
                modelpt3[i, 0] = lamda * (model_sheyingceliang_third[i, 0] - kappa * model_sheyingceliang_third[i, 1] - fai * model_sheyingceliang_third[i, 2]) + delta_x;
                modelpt3[i, 1] = lamda * (kappa * model_sheyingceliang_third[i, 0] + model_sheyingceliang_third[i, 1] - omiga * model_sheyingceliang_third[i, 2]) + delta_y;
                modelpt3[i, 2] = lamda * (fai * model_sheyingceliang_third[i, 0] + omiga * model_sheyingceliang_third[i, 1] + model_sheyingceliang_third[i, 2]) + delta_z;
            }

            //模型点大地坐标
            double[,] model_Pt1 = new double[15, 3];
            double[,] model_Pt2 = new double[8, 3];
            double[,] model_Pt3 = new double[11, 3];

            //将地面摄影测量坐标转换为大地坐标

            richTextBox5.Text += "701——702" + "\n";
            richTextBox5.Text += "点号       X坐标                 Y坐标                Z坐标 " + "\n";

            for (int i = 0; i < 15; i++)
            {
                model_Pt1[i, 0] = (b * modelpt1[i, 0] + a * modelpt1[i, 1]) / (lamda1 * lamda1) + XControl[0];
                model_Pt1[i, 1] = (a * modelpt1[i, 0] - b * modelpt1[i, 1]) / (lamda1 * lamda1) + YControl[0];
                model_Pt1[i, 2] = modelpt1[i, 2] / lamda1 + ZControl[0];
            }
            for (int i = 0; i < 15; i++)
            {
                richTextBox5.Text += String.Format("{0, -5}", points1_Name[i]) + "  " + String.Format("{0, -19}", model_Pt1[i, 0].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt1[i, 1].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt1[i, 2].ToString("F4")) + "\n";
            }

            richTextBox5.Text += "\n";
            richTextBox5.Text += "702——703" + "\n";
            richTextBox5.Text += "点号       X坐标                 Y坐标                Z坐标 " + "\n";

            for (int i = 0; i < 8; i++)
            {
                model_Pt2[i, 0] = (b * modelpt2[i, 0] + a * modelpt2[i, 1]) / (lamda1 * lamda1) + XControl[0];
                model_Pt2[i, 1] = (a * modelpt2[i, 0] - b * modelpt2[i, 1]) / (lamda1 * lamda1) + YControl[0];
                model_Pt2[i, 2] = modelpt2[i, 2] / lamda1 + ZControl[0];
            }
            for (int i = 0; i < 8; i++)
            {
                richTextBox5.Text += String.Format("{0, -5}", points2_Name[i]) + "  " + String.Format("{0, -19}", model_Pt2[i, 0].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt2[i, 1].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt2[i, 2].ToString("F4")) + "\n";
            }

            richTextBox5.Text += "\n";
            richTextBox5.Text += "703——704" + "\n";
            richTextBox5.Text += "点号       X坐标                 Y坐标                Z坐标 " + "\n";

            for (int i = 0; i < 11; i++)
            {
                model_Pt3[i, 0] = (b * modelpt3[i, 0] + a * modelpt3[i, 1]) / (lamda1 * lamda1) + XControl[0];
                model_Pt3[i, 1] = (a * modelpt3[i, 0] - b * modelpt3[i, 1]) / (lamda1 * lamda1) + YControl[0];
                model_Pt3[i, 2] = modelpt3[i, 2] / lamda1 + ZControl[0];
            }
            for (int i = 0; i < 11; i++)
            {
                richTextBox5.Text += String.Format("{0, -5}", points3_Name[i]) + "  " + String.Format("{0, -19}", model_Pt3[i, 0].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt3[i, 1].ToString("F4")) + "  " + String.Format("{0, -19}", model_Pt3[i, 2].ToString("F4")) + "\n";
            }

            //大地坐标系下的检查点坐标
            double[] checkpoint = new double[5];
            double[] checkP_Xt = new double[5];
            double[] checkP_Yt = new double[5];
            double[] checkP_Zt = new double[5];

            //检查点的误差
            double[] checkP_dx = new double[5];
            double[] checkP_dy = new double[5];
            double[] checkP_dz = new double[5];

            //读取检查点的坐标
            //检查点为四个包含在像对中的地面点的已知坐标，用来检测计算结果精度
            string[] l = richTextBox3.Text.Split('\n');
            for (int i = 0; i < l.Length; i++)
            {
                string[] Data = l[i].Split(' ');
                checkpoint[i] = double.Parse(Data[0]);
                checkP_Xt[i] = double.Parse(Data[1]);
                checkP_Yt[i] = double.Parse(Data[2]);
                checkP_Zt[i] = double.Parse(Data[3]);
            }

            //求检查点与控制点坐标的差值
            checkP_dx[0] = model_Pt1[12, 0] - checkP_Xt[0];
            checkP_dy[0] = model_Pt1[12, 1] - checkP_Yt[0];
            checkP_dz[0] = model_Pt1[12, 2] - checkP_Zt[0];

            checkP_dx[1] = model_Pt1[2, 0] - checkP_Xt[1];
            checkP_dy[1] = model_Pt1[2, 1] - checkP_Yt[1];
            checkP_dz[1] = model_Pt1[2, 2] - checkP_Zt[1];

            checkP_dx[2] = model_Pt1[4, 0] - checkP_Xt[2];
            checkP_dy[2] = model_Pt1[4, 1] - checkP_Yt[2];
            checkP_dz[2] = model_Pt1[4, 2] - checkP_Zt[2];

            checkP_dx[3] = model_Pt1[3, 0] - checkP_Xt[3];
            checkP_dy[3] = model_Pt1[3, 1] - checkP_Yt[3];
            checkP_dz[3] = model_Pt1[3, 2] - checkP_Zt[3];

            checkP_dx[4] = model_Pt2[1, 0] - checkP_Xt[4];
            checkP_dy[4] = model_Pt2[1, 1] - checkP_Yt[4];
            checkP_dz[4] = model_Pt2[1, 2] - checkP_Zt[4];

            //将检查的结果输出
            richTextBox6.Text += "点号       X坐标差               Y坐标差             Z坐标差\n";
            for (int i = 0; i < l.Length; i++)
            {
                richTextBox6.Text += String.Format("{0, -4}", checkpoint[i]) + "  " + String.Format("{0, -19}", checkP_dx[i].ToString("F4")) + "  " + String.Format("{0, -19}", checkP_dy[i].ToString("F4")) + "  " + String.Format("{0, -19}", checkP_dz[i].ToString("F4")) + "\n";
            }
        }


        public void XDDX(int point_count, double[] x1, double[] y1, double[] x2, double[] y2, //同名像点的左右平面坐标
                                double[,] dx, //相对方位元素改正数（dx）
                                double[,] X,  //相对方位元素
                                double[] Xm, double[] Ym, double[] Zm, //模型点在像空辅中的坐标
                                double[] N1, double[] N2,   //两个点投影系数
                                double[] X1, double[] Y1, double[] Z1, double[] Y2, //像点的像空间辅助坐标
                                ref double bX, ref double bY, ref double bZ) //摄影基线分量
        {//像对定向函数
            double by, bz;
            double[] X2 = new double[point_count];
            double[] Z2 = new double[point_count];

            //R矩阵的计算过程，带入公式得到9个系数
            double a11 = Math.Cos(X[2, 0]) * Math.Cos(X[4, 0]) - Math.Sin(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Sin(X[4, 0]);
            double a12 = -Math.Cos(X[2, 0]) * Math.Sin(X[4, 0]) - Math.Sin(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Cos(X[4, 0]);
            double a13 = -Math.Sin(X[2, 0]) * Math.Cos(X[3, 0]);
            double b11 = Math.Cos(X[3, 0]) * Math.Sin(X[4, 0]);
            double b12 = Math.Cos(X[3, 0]) * Math.Cos(X[4, 0]);
            double b13 = -Math.Sin(X[3, 0]);
            double c11 = Math.Sin(X[2, 0]) * Math.Cos(X[4, 0]) + Math.Cos(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Sin(X[4, 0]);
            double c12 = -Math.Sin(X[2, 0]) * Math.Sin(X[4, 0]) + Math.Cos(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Cos(X[4, 0]);
            double c13 = Math.Cos(X[2, 0]) * Math.Cos(X[3, 0]);

            //通过旋转矩阵，将像空间直角坐标系转换为像空间辅助坐标系
            for (int i = 0; i < point_count; i++)
            {
                X1[i] = (a11 * x1[i] + a12 * y1[i] - a13 * f);
                Y1[i] = (b11 * x1[i] + b12 * y1[i] - b13 * f);
                Z1[i] = (c11 * x1[i] + c12 * y1[i] - c13 * f);
            }

            //定义观测值Q
            double[,] Q = new double[point_count, 1];
            int cirnum = 0;
            for (int k = 0; ; k++)
            {
                //右片的旋转矩阵R2
                double a1 = Math.Cos(X[2, 0]) * Math.Cos(X[4, 0]) - Math.Sin(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Sin(X[4, 0]);
                double a2 = -Math.Cos(X[2, 0]) * Math.Sin(X[4, 0]) - Math.Sin(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Cos(X[4, 0]);
                double a3 = -Math.Sin(X[2, 0]) * Math.Cos(X[3, 0]);
                double b1 = Math.Cos(X[3, 0]) * Math.Sin(X[4, 0]);
                double b2 = Math.Cos(X[3, 0]) * Math.Cos(X[4, 0]);
                double b3 = -Math.Sin(X[3, 0]);
                double c1 = Math.Sin(X[2, 0]) * Math.Cos(X[4, 0]) + Math.Cos(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Sin(X[4, 0]);
                double c2 = -Math.Sin(X[2, 0]) * Math.Sin(X[4, 0]) + Math.Cos(X[2, 0]) * Math.Sin(X[3, 0]) * Math.Cos(X[4, 0]);
                double c3 = Math.Cos(X[2, 0]) * Math.Cos(X[3, 0]);

                //同理，通过旋转矩阵R2得到右边相片像空间辅助坐标系
                for (int i = 0; i < point_count; i++)
                {
                    //MessageBox.Show(Convert.ToString(i));
                    X2[i] = a1 * x2[i] + a2 * y2[i] + a3 * (-f);
                    Y2[i] = b1 * x2[i] + b2 * y2[i] + b3 * (-f);
                    Z2[i] = c1 * x2[i] + c2 * y2[i] + c3 * (-f);
                }

                //bx乘以相对方位元素得到by和bz
                by = bx * X[0, 0]; bz = bx * X[1, 0];
                //通过得到的各数计算点投影系数N1 N2以及观测值Q
                for (int i = 0; i < point_count; i++)
                {
                    N1[i] = (bx * Z2[i] - bz * X2[i]) / (X1[i] * Z2[i] - X2[i] * Z1[i]);
                    N2[i] = (bx * Z1[i] - bz * X1[i]) / (X1[i] * Z2[i] - X2[i] * Z1[i]);
                    Q[i, 0] = N1[i] * Y1[i] - N2[i] * Y2[i] - by;
                }
                //组成误差方程式
                //先对系数矩阵B进行计算
                double[,] B = new double[point_count, 5];
                for (int i = 0; i < point_count; i++)
                {
                    B[i, 0] = bx;
                    B[i, 1] = -Y2[i] / Z2[i] * bx;
                    B[i, 2] = -X2[i] * Y2[i] * N2[i] / Z2[i];
                    B[i, 3] = -(Z2[i] + Y2[i] * Y2[i] / Z2[i]) * N2[i];
                    B[i, 4] = X2[i] * N2[i];
                }

                //解算法方程
                double[,] BT = new double[7, 12];//系数阵B的转置
                BT = myMatrix.Matrix_Transpose(B);
                double[,] BTB = new double[7, 7]; //BT*B
                BTB = myMatrix.Matrix_Multiply(BT, B);
                double[,] BTBN = new double[7, 7]; //BT*B的逆矩阵
                BTBN = myMatrix.Matrix_Reverse(BTB);
                double[,] BTBNBT = new double[7, 12]; //BT*B的逆矩阵乘B的转置
                BTBNBT = myMatrix.Matrix_Multiply(BTBN, BT);
                //得到改正数
                dx = myMatrix.Matrix_Multiply(BTBNBT, Q);
                
                //限制迭代次数
                if (cirnum >= 100)
                {
                    for (int i = 0; i < 5; i++)
                    {
                        X[i, 0] = X[i, 0] + dx[i, 0];
                    }
                    break;
                }
                //加上改正数 得到方位元素新值
                else
                {
                    for (int i = 0; i < 5; i++)
                    {
                        X[i, 0] = X[i, 0] + dx[i, 0];
                    }
                }
                cirnum = cirnum + 1;

            }

            //计算地面点的像空间辅助坐标
            for (int j = 0; j < point_count; j++)
            {
                Xm[j] = N1[j] * X1[j];
                Ym[j] = 0.5 * (N1[j] * Y1[j] + N2[j] * Y2[j] + by);
                Zm[j] = N1[j] * Z1[j];
            }
            bZ = bz;
            bY = by;
            bX = bx;
        }       
    }
}

以下是矩阵计算模块：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace Analytic_aerial_triangulation
{
    class MatrixOperations
    {
        //1、矩阵减法
        public double[,] Matr_Sub(double[,] Matr1, double[,] Matr2)
        {
            int row = Matr1.GetLength(0);
            int column = Matr1.GetLength(1);
            double[,] Matr_Output = new double[row, column];
            for (int i = 0; i < row; i++)
            {
                for (int j = 0; j < column; j++)
                {
                    Matr_Output[i, j] = Matr1[i, j] - Matr2[i, j];  //对应位置相减
                }
            }
            return Matr_Output;
        }

        //2、矩阵求转置，误差方程中的B系数矩阵需要用到转置
        public double[,] Matrix_Transpose(double[,] Matr1)
        {
            int row = Matr1.GetLength(0);
            int column = Matr1.GetLength(1);
            double[,] Matr_Output = new double[column, row];   //新定义一个矩阵，与原矩阵的行数和列数相反
            for (int i = 0; i < column; i++)
            {
                for (int j = 0; j < row; j++)
                {
                    Matr_Output[i, j] = Matr1[j, i];   //新矩阵和原矩阵的行列对应位置进行新值的赋值
                }
            }
            return Matr_Output;
        }

        //3、矩阵乘法
        public double[,] Matrix_Multiply(double[,] Matr1, double[,] Matr2)  //矩阵乘法
        {
            //在误差方程中，计算两矩阵乘法时保证了前提是矩阵1的列等于矩阵2的行，故在此不再进行矩阵的行列是否相等判断
            //此处定义的row_2既为矩阵1的列也为矩阵2的行
            int row_1 = Matr1.GetLength(0);
            int column_2 = Matr2.GetLength(1);
            int row_2 = Matr2.GetLength(0);
            double[,] Matr_Output = new double[row_1, column_2];  //定义结果矩阵
            for (int i = 0; i < row_1; i++)
            {
                for (int j = 0; j < column_2; j++)
                {
                    for (int k = 0; k < row_2; k++)
                    {
                        Matr_Output[i, j] += Matr1[i, k] * Matr2[k, j];   //k为新矩阵的列定位，通过此项定位确定结果位置
                    }
                }
            }
            return Matr_Output;
        }

        //4、矩阵行列式计算
        public double Matrix_Value(double[,] Matr1, int level)
        {
            double[,] Matr_MidResult = new double[level, level];  //确定一个新的固定行列数的矩阵
            for (int i = 0; i < level; i++)
            {
                for (int j = 0; j < level; j++)
                {
                    Matr_MidResult[i, j] = Matr1[i, j];  //将原有矩阵赋给新矩阵进行后续计算
                }
            }

            double MidValue, MidResultValue;
            int PositiveNumberJudge = 1;
            for (int i = 0, j = 0; i < level && j < level; i++, j++)
            {
                if (Matr_MidResult[i, j] == 0)
                {
                    int point_count = i;
                    for (; Matr_MidResult[point_count, j] == 0; point_count++) ;
                    if (point_count == level)
                    {
                        return 0;  //找到最后一行时停止计算
                    }
                    else
                    {
                        for (int n = j; n < level; n++)
                        {
                            MidValue = Matr_MidResult[i, n];
                            Matr_MidResult[i, n] = Matr_MidResult[point_count, n];
                            Matr_MidResult[point_count, n] = MidValue;
                        }
                        PositiveNumberJudge *= (-1);
                    }
                }
                for (int s = level - 1; s > i; s--)
                {
                    MidResultValue = Matr_MidResult[s, j];
                    for (int t = j; t < level; t++)
                    {
                        Matr_MidResult[s, t] -= Matr_MidResult[i, t] * (MidResultValue / Matr_MidResult[i, j]);
                    }
                }
            }
            double ChangelessValue = 1;
            for (int i = 0; i < level; i++)
            {
                if (Matr_MidResult[i, i] != 0)
                {
                    ChangelessValue *= Matr_MidResult[i, i];
                }
                else
                {
                    return (0);
                }
            }
            return PositiveNumberJudge * ChangelessValue;
        }

        //5、矩阵求逆
        public double[,] Matrix_Reverse(double[,] dMatrix)
        {
            int Level = dMatrix.GetLength(0);
            double ReverseValue, CalculationValue;
            double SubMatrix = Matrix_Value(dMatrix, Level);
            if (SubMatrix == 0)
            {
                return null;
            }
            double[,] MatrixReturn = new double[Level, 2 * Level];
            for (int i = 0; i < Level; i++)
            {
                for (int j = 0; j < 2 * Level; j++)
                {
                    if (j < Level)
                    {
                        MatrixReturn[i, j] = dMatrix[i, j];
                    }
                    else
                    {
                        MatrixReturn[i, j] = 0;
                    }
                }
                MatrixReturn[i, Level + i] = 1;
            }
            for (int i = 0, j = 0; i < Level && j < Level; i++, j++)
            {
                if (MatrixReturn[i, j] == 0)
                {
                    int point_count = i;
                    for (; dMatrix[point_count, j] == 0; point_count++) ;
                    if (point_count == Level)
                    {
                        return null;
                    }
                    else
                    {
                        for (int n = j; n < 2 * Level; n++)
                        {
                            MatrixReturn[i, n] += MatrixReturn[point_count, n];
                        }
                    }
                }
                ReverseValue = MatrixReturn[i, j];
                if (ReverseValue != 1)
                {
                    for (int n = j; n < 2 * Level; n++)
                    {
                        if (MatrixReturn[i, n] != 0)
                        {
                            MatrixReturn[i, n] /= ReverseValue;
                        }
                    }
                }
                for (int s = Level - 1; s > i; s--)
                {
                    ReverseValue = MatrixReturn[s, j];
                    for (int t = j; t < 2 * Level; t++)
                    {
                        MatrixReturn[s, t] -= (MatrixReturn[i, t] * ReverseValue);
                    }
                }
            }
            for (int i = Level - 2; i >= 0; i--)
            {
                for (int j = i + 1; j < Level; j++)
                {
                    if (MatrixReturn[i, j] != 0)
                    {
                        CalculationValue = MatrixReturn[i, j];
                        for (int n = j; n < 2 * Level; n++)
                        {
                            MatrixReturn[i, n] -= (CalculationValue * MatrixReturn[j, n]);
                        }
                    }
                }
            }
            double[,] Matrix_Return = new double[Level, Level];
            for (int i = 0; i < Level; i++)
            {
                for (int j = 0; j < Level; j++)
                {
                    Matrix_Return[i, j] = MatrixReturn[i, j + Level];
                }
            }
            return Matrix_Return;
        }
    }
}

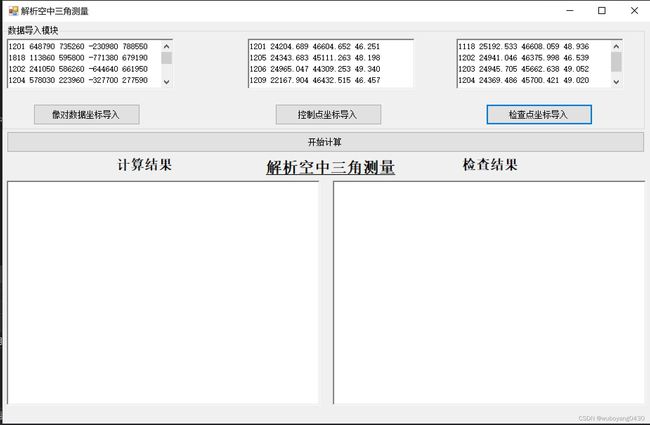
以下是窗体界面以供参考：
主要用到richTextBox和button

欢迎大家在评论区留言，后续也会根据大家的建议进一步优化代码。