动态规划设计：最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）

动态规划的核心设计思想是数学归纳法。

相信大家对数学归纳法都不陌生，高中就学过，而且思路很简单。比如我们想证明一个数学结论，那么我们先假设这个结论在 `k < n` 时成立，然后根据这个假设，想办法推导证明出 `k = n` 的时候此结论也成立。如果能够证明出来，那么就说明这个结论对于 `k` 等于任何数都成立。

类似的，我们设计动态规划算法，不是需要一个 dp 数组吗？我们可以假设 `dp[0...i-1]` 都已经被算出来了，然后问自己：怎么通过这些结果算出 `dp[i]`？

直接拿最长递增子序列这个问题举例你就明白了。不过，首先要定义清楚 dp 数组的含义，即 `dp[i]` 的值到底代表着什么？

我们的定义是这样的：`dp[i]` 表示以 `nums[i]` 这个数结尾的最长递增子序列的长度。

根据这个定义，我们就可以推出 base case：`dp[i]` 初始值为 1，因为以 `nums[i]` 结尾的最长递增子序列起码要包含它自己。

举两个例子：

根据这个定义，我们的最终结果（子序列的最大长度）应该是 dp 数组中的最大值。

int res = 0;
for (int i = 0; i < dp.length; i++) {
    res = Math.max(res, dp[i]);
}
return res;

你也许会问，刚才的算法演进过程中每个 `dp[i]` 的结果是我们肉眼看出来的，我们应该怎么设计算法逻辑来正确计算每个 `dp[i]` 呢？

这就是动态规划的重头戏，如何设计算法逻辑进行状态转移，才能正确运行呢？这里需要使用数学归纳的思想：

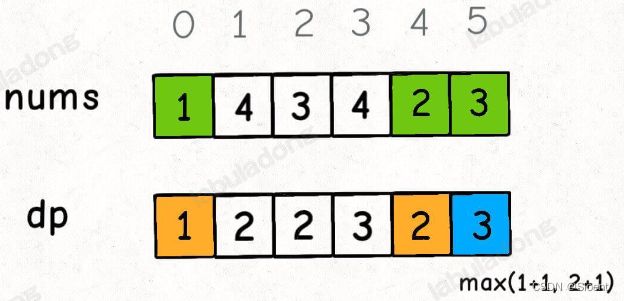
假设我们已经知道了 `dp[0..4]` 的所有结果，我们如何通过这些已知结果推出 `dp[5]` 呢？

根据刚才我们对 `dp` 数组的定义，现在想求 `dp[5]` 的值，也就是想求以 `nums[5]` 为结尾的最长递增子序列。

`nums[5] = 3`，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到这些子序列末尾，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

`nums[5]` 前面有哪些元素小于 `nums[5]`？这个好算，用 for 循环比较一波就能把这些元素找出来。

以这些元素为结尾的最长递增子序列的长度是多少？回顾一下我们对 `dp` 数组的定义，它记录的正是以每个元素为末尾的最长递增子序列的长度。

以我们举的例子来说，`nums[0]` 和 `nums[4]` 都是小于 `nums[5]` 的，然后对比 `dp[0]` 和 `dp[4]` 的值，我们让 `nums[5]` 和更长的递增子序列结合，得出 `dp[5] = 3`：

for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

当 `i = 5` 时，这段代码的逻辑就可以算出 `dp[5]`。其实到这里，这道算法题我们就基本做完了。

你也许会问，我们刚才只是算了 `dp[5]` 呀，`dp[4]`, `dp[3]` 这些怎么算呢？类似数学归纳法，你已经可以算出 `dp[5]` 了，其他的就都可以算出来：

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        // 寻找 nums[0..j-1] 中比 nums[i] 小的元素
        if (nums[i] > nums[j]) {
            // 把 nums[i] 接在后面，即可形成长度为 dp[j] + 1，
            // 且以 nums[i] 为结尾的递增子序列
            dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
}

结合我们刚才说的 base case，下面我们看一下完整代码：

int lengthOfLIS(int[] nums) {
    // 定义：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
    int[] dp = new int[nums.length];
    // base case：dp 数组全都初始化为 1
    Arrays.fill(dp, 1);
    for (int i = 0; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) 
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
    
    int res = 0;
    for (int i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

至此，这道题就解决了，时间复杂度 `O(N^2)`。总结一下如何找到动态规划的状态转移关系：

1、明确 `dp` 数组的定义。这一步对于任何动态规划问题都很重要，如果不得当或者不够清晰，会阻碍之后的步骤。

2、根据 `dp` 数组的定义，运用数学归纳法的思想，假设 `dp[0...i-1]` 都已知，想办法求出 `dp[i]`，一旦这一步完成，整个题目基本就解决了。

但如果无法完成这一步，很可能就是 `dp` 数组的定义不够恰当，需要重新定义 `dp` 数组的含义；或者可能是 `dp` 数组存储的信息还不够，不足以推出下一步的答案，需要把 `dp` 数组扩大成二维数组甚至三维数组。