PID校正

一、Introduction to PID Control

PID控制是一种应用非常广泛的控制算法。小到控制一个元件的温度，大到控制无人机的飞行姿态和飞行速度等等，都可以使用PID控制。PID(proportion integration differentiation)其实就是指比例，积分，微分控制，当得到系统的输出后，将输出经过比例、积分、微分3种运算，叠加到输入中，从而控制系统的行为[1]。

PID控制理念最早提出是在1932年，由Nyquist在一篇论文当中提出了采用图形的方法来判断系统的稳定性。在他的基础上，H. W. Bode等人建立了一整套在频域范围设计反馈放大器的方法，后被用于自动控制系统的分析和设计，这也是PID算法最早从书面走向实践。与此同时，反馈控制原理开始应用于工业过程中。1936年英国的考伦德（A Callender）和斯蒂文森（A Stevenson）等人给出了 PID控制器的方法，自此PID算法正式形成了，并且后来在自动控制技术中占有非常重要的地位[2]。

PID校正装置是用比例(Proportional)、积分(Integral)和微分(Derivative)控制规律组成的串联校正装置，使用方便，适应性强，易于工程实现。而且根据需要，可以变形为P、PI或PID等类型调节器。目前在理论上已经证明，对于过程控制的典型对象——“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。

二、Principles of PID Control and PID Parameters

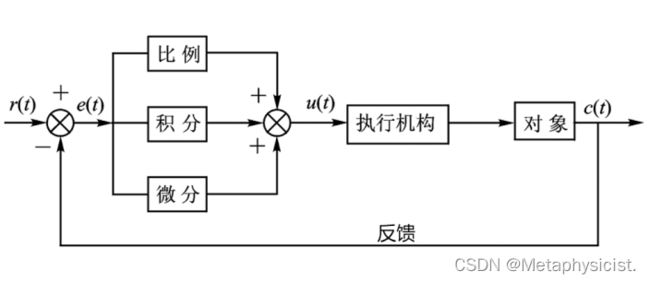
PID控制的主要过程是通过对被控对象的当前值进行采样，并计算采样值与期望值的偏差，再将这个偏差反馈给PID控制器，从而调整对被控对象的输入（执行器的输出）。这里的偏差指给定量与反馈量之差，可以量测；而我们常说的误差为系统输出的实际值与期望值之差，无法量测，只有数学意义。偏差存在极性，有正偏差和负偏差之分。

PID控制器（比例-积分-微分控制器），由比例单元(Proportion)、积分单元(Integral)和微分单元(Derivative)组成，通过Kp， Ki和Kd三个参数进行设定。

Kp（比例系数）代表了当前的信息，起纠正偏差的作用，使反应迅速；

Kd（微分系数）代表了将来的信息，在过程开始时强迫过程进行，过程结束时减小超调，克服振荡，提高系统的稳定性，加快系统的过渡过程；

Ki（积分系数）代表了过去积累的信息，它能消除静差，改善系统的静态特性。

采用PID调节器，往往并不需要知道于控制对象的精确数学模型，这是它的优点，但也正因如此，其参数通常也都是根据经验在线整定，以便得到满意的控制效果[3][4]。

三、Parameter tuning of PID controller

PID调节器各增益参数增加对系统时域指标的影响如下[5]：

需要设定的值有：

·目标值（Setpoint）
·pid参数（Kp，Ki，Kd）
·输出极限（Output Limits）
·采样时间（Sample Time）

PID控制整定法有理论计算法和经验整定法两种。

经验法

首先需要注意的是，由于闭环调节的影响因素，PID参数是无法通过数学建模的方式获取的，只有通过实际调试获得参数。即便如此，我们仍可以给出一些保守的PID参数作为初值，见下表：

一般采用的是临界比例法（属于工程整定法）。

工程整定法主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。（简单来讲就是试凑）[1]。

临界比例法

一般采用的是临界比例法（属于工程整定法）。

工程整定法主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。（简单来讲就是试凑）。

PID调节的实质在于取得快速性和稳定性的折中，利用该方法进行PID控制器参数的整定步骤如下：

(1)首先预选择一个足够短的采样时间让系统工作，输入设定为系统允许的最大值（输出极限）的60%~70%。 控制时间根据实际工艺过程决定，一般默认1s，通常建议先从默认值开始，再根据结果进行调整，由于电机PID调节无滞后，顾在效果不佳的情况下也可尝试缩短采样时间。

(2)仅加入P比例控制环节。 当手动调节PID控制器时，通常按照P，I，D的顺序调整参数。初调时，Kp选小一些，这是为了尽可能减小比例作用；然后慢慢调大，直到系统对输入的阶跃信号（Step Function）出现临界振荡，记下这时的比例放大系数和临界振荡周期。如果后续需要加入积分控制环节，则需设定Kp为当前值的60%~70%，这是因为当Kp调整至接近期望值后，Ki就开始减少到合适值，这会导致稳定性的降低，反过来Ki又需要减少；

临界是介于收敛和发散的一种过渡状态。临界振荡指等幅振荡。

(3)加入I积分控制环节。 积分系数初调时要把积分时间设置长些，这是为了减小积分作用；然后慢慢调小直到系统稳定为止，设定PID的积分时间常数Ti为当前值的150%~180%。

一般情况下到此为止

(4)D微分控制环节一般不用设定，待整定参数越多，则整定难度越大。如果通过比例、积分参数的调节还是收不到理想的控制要求，才调节微分时间。初调时把这个系数设小，然后慢慢调大，直到系统稳定。除了会导致调参复杂，不使用微分控制环节的原因是其易受噪声和其它扰动影响，并将其放大到更大的程度，导致稳定性降低。

References

[1] 线性系统的矫正方法——PID控制理论. CSDN.

[2] The PID Controller & Theory Explained. NI.com.

[3] PID控制算法原理（抛弃公式，从本质上真正理解PID控制）. zhihu.com.

[4] PID控制. 古月居.

[5] Kiam Heong Ang, G. Chong and Yun Li, "PID control system analysis, design, and technology," in IEEE Transactions on Control Systems Technology, vol. 13, no. 4, pp. 559-576, July 2005, doi: 10.1109/TCST.2005.847331.

附录：用matlab实现倒立摆的pid控制

% 倒立摆PID控制程序

% 参数设置
m = 0.5;  % 摆杆质量
l = 0.25;  % 摆杆长度
g = 9.81;  % 重力加速度
I = m * l^2;  % 摆杆惯性矩

% 目标角度和初始角度
theta_desired = pi/4;  % 目标角度设定为45度
theta0 = 0;  % 初始角度为0度

% PID控制器参数
Kp = 10;  % 比例增益
Ki = 5;  % 积分增益
Kd = 2;  % 微分增益

% 时间步长和模拟时间
dt = 0.01;  % 时间步长
t_sim = 5;  % 模拟时间

% 初始化变量
theta = zeros(1, t_sim/dt + 1);  % 角度数组
theta_dot = zeros(1, t_sim/dt + 1);  % 角速度数组
theta_error = zeros(1, t_sim/dt + 1);  % 角度误差数组
theta_integral = 0;  % 角度误差积分
theta_prev = theta0;  % 上一时刻的角度

% 模拟
for t = 0:dt:t_sim
    % 计算角度误差和积分项
    theta_error_current = theta_desired - theta_prev;
    theta_integral = theta_integral + theta_error_current * dt;
    
    % 计算控制信号
    u = Kp * theta_error_current + Ki * theta_integral + Kd * (theta_error_current - theta_error(end))/dt;
    
    % 计算角度加速度
    theta_acc = (m * g * l * sin(theta_prev) - u) / I;
    
    % 更新角度和角速度
    theta_dot_next = theta_dot(end) + theta_acc * dt;
    theta_next = theta_prev + theta_dot_next * dt;
    
    % 更新变量
    theta(end+1) = theta_next;
    theta_dot(end+1) = theta_dot_next;
    theta_error(end+1) = theta_error_current;
    theta_prev = theta_next;
end

% 绘制图形
t = 0:dt:t_sim;
plot(t, theta);
xlabel('Time');
ylabel('Angle');
title('Inverted Pendulum PID Control');