【数据结构】72变的双端队列

前言

大家好，很高兴又和大家见面啦！！！
在前面的篇章中，咱们详细介绍了队列这种新的数据结构，现在我们简单的回顾一下队列的三要素——数据的逻辑结构、数据的存储结构以及数据的运算。

数据的逻辑结构

• 队列的数据元素在逻辑上是呈现线性结构，也就是说队列也是一种线性表，只不过是一种操作受限的线性表。

数据的存储结构

• 队列中的数据元素在内存空间中可以通过顺序存储和链式存储两种方式进行存储。
• 通过顺序存储实现的队列我们称之为循环队列，循环队列的空间大小是不可改变的，循环的实现是通过取模运算实现数组下标的循环；
• 通过链式存储实现的队列我们称之为链队列，链队列是通过队头指针与队尾指针分别指向单链表的表头与表尾进行实现；

数据的运算

• 在逻辑结构上队列是属于一种操作受限的线性表，队列中的元素只能从一端已进行插入，从另一端进行删除，因此我们可以定义在队列上的基本操作有：
  • 创建、销毁、从队尾进行增加、从队头进行删除、判空、查找队头元素；
• 在存储结构上队列在不同的存储结构下对各操作实现的方式也有区别：
  • 顺序存储：在顺序存储中，我们进行增加与删除的操作是通过队头指针与队尾指针存储的数组下标的修改来实现的，因为数组的大小是预先申请好的，因此在顺序存储中我们还需要对队列进行判满的操作，根据不同的满队条件，我们可以进行三种方式来实现队列——空间置换法、队长法以及标志法；
  • 链式存储：在链式存储中，队列对空间的使用更加的灵活，理论上将只要内存空间足够大，队列就不会出现满队的情况。在链式存储的实现中我们在定义数据类型时要将队列中各个结点的数据类型与队列的数据类型分开定义，确保我们创建的队列是通过头尾指针指向各个结点的队列。

到这里队列的三要素我们就已经复习完了。

在今天的内容中，我们将介绍一个武艺高超的队列——双端队列。它的武艺究竟高超在什么地方呢？下面我们一下来看一下吧！

一、双端队列

1.1 双端队列的定义

双端队列指的是运行在两端进行入队与出队操作的队列，其元素的逻辑结构依然是线性结构。在双端队列中我们将队列的两端分别称为前端和后端，两端都可以进行入队和出队。如下所示：

在双端队列中由于它的前端与后端都能进行入队和出队，因此进行出队入队的元素满足下面的规则：

• 从前端进的元素排列在队列后端进的元素的前面；
• 从后端进的元素排列在队列前端进的元素的后面；
• 无论是前端还是后端出队，先出的元素排列在后出的元素的前面。

在双端队列中，因为它的前端和后端都能够实现入队和出队，所以他会有不同的操作形式：

• 当我们只看前端或者只看后端的话，我们就会发现，它其实是一个栈，因为只从一端进行入队和出队时，元素满足后进先出(LIFO)的操作特性；
• 当我们只要求元素从前端进后端出，或者从后端进前端出的话，它此时就是一个队列，因为此时的双端队列满足先进先出(FIFO)的操作特性；

也就是说双端队列我们可以看做是栈和队列的结合体，那如果我们限制双端队列一端的输入或输出会是怎么样呢？下面我们一起来探讨一下；

1.2 输入受限的双端队列

当我们只允许双端队列的一端进行输入时，此时双端队列就会变成如下结构：

在这种情况下队列中的元素在入队时是只能从一端入队，但是出队不受限制，所以这种形式的双端队列满足以下操作特性：

• 对于允许入队的一端来说，元素满足后入先出(LIFO)的操作特性；
• 对于入队受限的一端来说，元素满足先入先出(FIFO)的操作特性；

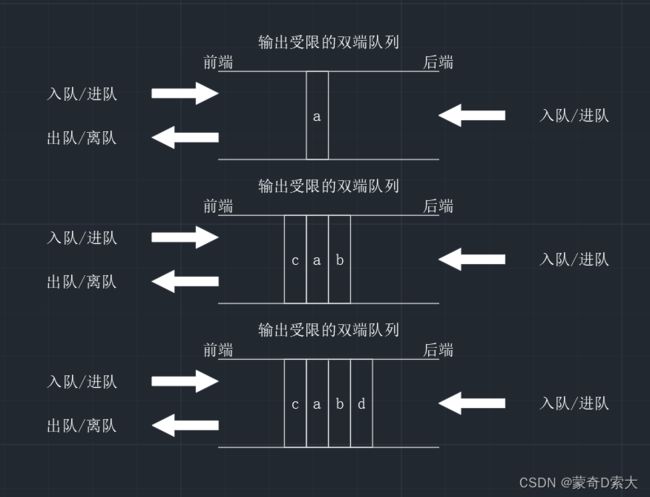
1.3 输出受限的双端队列

当我们只允许双端队列的一端输出时，此时的双端队列就会变成如下结构：

在这种情况下，双端队列只能从一端进行出队，入队不受影响，因此这种形式的双端队列满足以下操作特性：

• 在允许出队的一端，元素满足LIFO的操作特性；
• 在出队受限的一端，元素满足FIFO的操作特性；

1.5 输入输出都受限的双端队列

当我们只允许双端队列中的元素从哪一端进就从哪一端出的话，此时的双端队列就会变成两个栈底相邻的栈，如下所示：

在这种情况下不管是从前端入队的元素还是从后端入队的元素都满足LIFO的操作特性。

这时可能有朋友会说，我能不能限制只能从一端进从另一端出呢？就如下面这样：

从上图可以看到，如果只能限制从一端进另一端出的话，我们会发现此时的双端队列如果两个端都有元素入队的话，此时是没办法出队的，因此，我们在双端队列中不能限制元素只能从一端进、从另一端出。

1.6 小结

从上面的介绍中我们可以得出以下结论：

1. 双端队列也是一种操作受限的线性表，它同时具有栈和队列的操作特性；
2. 当双端队列的一端的输入/输出受限时，受限制的一端的满足队列的操作特性，另一端满足栈的操作特性；
3. 当双端队列的输入和输出都受限时，此时的双端队列就会变成两个栈底相邻的栈。

介绍到这里，可能会有朋友有疑问了，我既然已经有了栈和队列这两种数据结构，现在将它们组合在一起是为什么呢？双端队列究竟有什么作用呢？下面我们就一起来探讨一下；

二、双端队列的使用

在数据结构这门科目中，目前我对双端队列的理解是——双端队列主要出现在元素的排序上，考试中一般也只是出现在选择题中，题目会要求我们判断四个选项中哪个选项符合双端队列的操作特性，或者不符合双端队列的操作特性。

下面我们通过【2010年的统考真题】来介绍双端队列的使用；

【2010统考真题】某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作，若元素a、b、c、d、e依次入此队列后再进行出队操作，则不可能得到的出队序列是（）。
A.b,a,c,d,e
B.d,b,a,c,e
C.d,b,c,a,e
D.e,c,b,a,d

对于这一道题，我们应该如何来求解呢？下面我将自己的解题思路分享给大家；

2.1 双端队列的出队序列——暴力求解

首先我先介绍的是一种比较基础的解法——暴力求解，何为暴力呢？就是将双端队列中的元素的所有情况全部列出来，比如，我要求解a，b，c，d四个元素在双端队列中的出队序列，如果我们要对4个元素进行排列组合的话，我就可以得到4!种，如下所示：

a,b,c,d    b,c,d,a    c,d,a,b    d,a,b,c
a,b,d,c    b,c,a,d    c,d,b,a    d,a,c,b
a,c,d,b    b,d,a,c    c,a,b,d    d,b,c,a
a,c,b,d    b,d,c,a    c,a,d,b    d,b,a,c
a,d,b,c    b,a,c,d    c,b,a,d    d,c,a,b
a,d,c,b    b,a,d,c    c,b,d,a    d,c,b,a

那是不是说这24中序列都是有效序列呢？下面我们就来逐个分析在不同形式的双端队列的情况下它们所能进行的排列组合的情况；

2.1.1 栈的出栈序列

对于双端队列而言，既然它是栈和队列的结合体，那么栈所满足的出队序列，双端队列一定满足，因此我们先来分析一下根据栈的特性，它能够得到哪些出队序列；

栈的操作特性是后入先出，那么对栈而言我们在保证abcd这四个元素时按顺序依次入栈的条件下，要想使元素d第一个出栈，那么abc的出栈顺序必然是cba，如下所示：

也就是说，如果我要让元素d第一个出栈，那么只会存在一种出栈序列——d,c,b,a；

同理，当我需要让元素c第一个出栈时，那对于元素b和元素a而言，它们的次序肯定是b先出栈，a再出栈，那我们就能得到3种序列——c,d,b,a/c,b,d,a/c,b,a,d；

当我们要让元素b先出栈时，此时第二个出栈的元素可以是a、c、d任意一个，当第二个出栈元素为d时，那么对于元素c和元素a来说，它们的出栈次序肯定是c先出，a后出，如下所示：

因此当以元素d先出栈时，我们可以得到5个出栈序列——b,a,c,d/b,a,d,c/b,c,a,d/b,c,d,a/b,d,c,a；

同理，当我们让a先出栈，d第二个出栈时，元素b和元素c的出栈顺序肯定是c,b，这里我就不演示了，也就是说此时我们也同样可以得到5个出栈序列——a,b,c,d/a,b,d,c/a,c,b,d/a,c,d,b/a,d,c,b；

对于栈而言，现在有以下这些序列是不满足栈的出栈序列的：
a,d,b,c/b,d,a,c/c,d,a,b/c,a,b,d/c,a,d,b/d,a,b,c/d,a,c,b/d,b,a,c/d,b,c,a/d,c,a,b
之所以不满足，就是因为出栈和入栈受到了限制，那如果在双端队列中，这些序列又会如何呢？

2.1.2 输入受限的双端队列

当在输入受限的双端队列中，输出是不受影响的，因此对于a,d,b,c这个序列而言它则可行起来了，如下所示：

因为两端都能出队，所以我只要按顺序进行入队，那么对于以a开始出队的序列是全部可行的，同样，此时以d开头的序列也会多出以下三种情况——d,a,b,c/d,a,c,b/d,c,a,b；

这是因为我们只能从一端输入，而要想使d先出队的话，那元素a,b,c肯定已经入队，之后我们才能开始进行出队操作；

同理，当我们想要让c先出队时，那元素a、b肯定已经入队，之后我们再进行出队操作的话，那对于序列c,a,b,c/c,a,d,b/c,d,a,b而言都是可以实现的了；

当我们想要让元素b先出队时，那对于b,d,a,c这个出队序列也是可以实现的了；

因此，在输入受限的双端队列中，只有d,b,a,c/d,b,c,a是无法实现的；

2.1.3 输出受限的双端队列

当在输出受限的双端队列中，我们要想得到对应的输出序列，只能够通过输入的方式来将其顺序进行排列，那在下面这些不满足栈的出栈序列中，又会有哪些是符合要求的呢？我们一起来看一下；
a,d,b,c/b,d,a,c/c,d,a,b/c,a,b,d/c,a,d,b/d,a,b,c/d,a,c,b/d,b,a,c/d,b,c,a/d,c,a,b

对于序列a,d,b,c而言，我们可以通过两端入队的方式来实现，如下所示：

同理，当b要先输出的话，那我们的输入输出顺序就是：a入队->b入队->b出队->c从受限制的一端入队->d入队——此时队列里的排列顺序是d,a,c。之后我们只需要依次执行出队就能得到b,d,a,c的出队次序了；

当c要先输出时，也就是说a和b已经入队了，下面我们来看一下如何实现c,d,a,b/c,a,b,d/c,a,d,b这三种情况的排序；

首先我们来看第一种——c,d,a,b，对应的出入队情况如下所示：

可以看到只要我们保证dab入队后的排列顺序就能完成对应的出队序列；

然后我们再来看一下c,a,b,d，对应的出入队情况如下所示：

可以看到在这种情况下我们可以通过输入端的不同完成对应的元素的排列顺序，然后依次出队即可；

接着我们再来看一下c,a,d,b，对应的出入队情况如下所示：

可以看到不管我们怎么进行输入，只要是c入队了，那a和b就肯定是已经入队了，因此a和b的出队顺序可以颠倒但是不可能会被隔开，因此在输出受限的双端队列中，这个出队序列是无法实现的。

同理，当d先出队时，我们只需要观察能不能通过入队的先后顺序来完成出队时的次序。此时有
d,a,b,c/d,a,c,b/d,b,a,c/d,b,c,a/d,c,a,b这五种情况等待我们验证，当d要第一个出队的话，那势必a,b,c都以完成了入队，也就是说，a和b的位置关系肯定是紧邻着的，那么我们就可以直接排除d,a,c,b和d,b,c,a这两种情况了。

因此在输出受限的双端队列中c,a,d,b/d,a,c,b/d,b,c,a这三种情况是无法实现的；

2.1.4 输入输出都受限的双端队列

当输入和输出都受限时，不管元素是从哪端进入，都是满足LIFO这个操作特性。在这种情况下
a,d,b,c/b,d,a,c/c,d,a,b/c,a,b,d/c,a,d,b/d,a,b,c/d,a,c,b/d,b,a,c/d,b,c,a/d,c,a,b这些输出序列又能不能实现呢？我们继续来看一下；

对于a,d,b,c这个输出序列，它的输入输出情况如下所示：

可以看到此时我们是可以通过不同端的输入来完成对应的出队次序的排列的，接下来只需要按照对应的次序进行出队即可；

下面我们再来看看b,d,a,c这种情况，对应的出入队情况如下所示：

可以看到通过两端的入队与出队也是能够实现对应的出队次序的；

下面我们再看看c,d,a,b/c,a,b,d/c,a,d,b这三种情况，如下所示：

可以看到，此时我们只要完成了前面两个元素的出队之后，后面两个元素的次序是可以颠倒的，因此以c为第一个出队元素的所有情况都是可以实现的；

接下来就是最关键的d了，因为d要先出队的话，那必须要将abc都先完成入队，在d,a,b,c/d,a,c,b/d,b,a,c/d,b,c,a/d,c,a,b这五种情况中，我们将其拆分成3种情况——da、db和dc，它们对应的出入队情况如下所示：

可以看到当要确保a是第二个出队时，那么b和c就不能和a在同一边，因此，b和c的出队顺序是一定的，所以对于d,a,b,c这种情况就不可能发生；

当第二个出队元素为b或者c时，此时我们都可以通过调整abc的入队位置来实现对应的出队序列，因此d,b,a,c/d,b,c,a/d,c,a,b这三种情况都是可以实现的；

所以在输出输入都受限时，只有d,a,b,c这种情况就不可能发生；

那如果我们不对输入和输出进行限制的话，我们会发现d,a,b,c也是可以实现的，如下所示：

也就是说，对于不受限制的双端队列它可能存在的出队情况就是n!

2.1.5 小结

现在我们已经介绍完了不同情况下的双端队列可能出现的出队次序，如果给这些元素的入队顺序进行编号的话，那么a,b,c,d的入队序号依次是1,2,3,4，现在我们可以根据这个入队序号做个总结：

• 在输入输出不受限制的双端队列中，元素可以以任意次序完成出队；
• 在输入受限的双端队列中，4号元素要先出队的话，1号元素与2号元素的出队一定是紧邻的；
• 在输出受限的双端队列中，当3号元素和4号元素要完成先出队的话，那么1号元素和2号的出队一定是紧邻的；
• 在输入输出都受限的双端队列中，当4号元素与1号元素要完成先后出队的话，那么2号元素和3号元素的出队顺序一定是32；
• 在栈中，当4号元素要在第一或者第二个进行出栈时，剩下的两个元素的出栈次序一定是满足LIFO；

现在对于4个元素的出入队情况我们就已经分析完了，可以看到，如果是元素比较少的情况下，这种暴力求解的方式也是不错的，但是如果遇到了如10年的真题卷一样的有5个元素时，我们如果使用这种方法的话明显是不合理的，那我们又应该如何处理呢？下面我就要介绍第二种方法——经验法；

2.2 双端队列的出队序列——经验法

经验法是根据暴力求解法的归纳总结，在介绍我的结论之前，我们先要思考一个问题，为什么会有这些不符合条件的情况发生？

我相信有朋友已经想到了，因为栈和队列操作特性的约束，栈中的元素要满足LIFO，而队列中的元素要满足FIFO，因此当元素是从一端入队，同一端出队时，元素的出队符合LIFO，当元素从一端入队另一端出队时，元素的出队符合FIFO；

在理解了这个点之后，再来看一下我对双端队列的个人理解与总结：

• 对于栈而言，越是入栈次序靠后的元素要先完成出栈时，它前面元素的出栈顺序一定是按照LIFO；
• 对于输入受限的双端队列，入队次序越靠后的元素要先完成出队，那次序越靠前的元素在进行出队时一定与入队次序紧跟它的元素相邻；
• 对于输出受限的双端队列，入队次序靠后的元素要先完成出队，那次序靠前的元素一定是紧邻的；
• 对于输入输出都受限的双端队列，入队次序越靠后的元素，与入队次序越靠前的元素进行先后出队时，中间的元素的出队次序一定是遵循LIFO；

根据这个结论，下面我们直接来看一下真题的题目：

【2010统考真题】某队列允许在其两端进行入队操作，但仅允许在一端进行出队操作，若元素a、b、c、d、e依次入此队列后再进行出队操作，则不可能得到的出队序列是（）。
A.b,a,c,d,e
B.d,b,a,c,e
C.d,b,c,a,e
D.e,c,b,a,d

从题目中我们可以得到结论，这是一个输出受限的双端队列，根据我们的结论，越是靠后的元素要先完成出队，次序靠前的元素一定是紧邻的。下面我们再来看选项：

• A选项中是以b为第一个出队元素进行的出队那么这个序列肯定是存在的，直接跳过；
• B和C选项都是以d为第一个出队元素，按照我们的结论，靠前的元素一定时紧邻的，也就是说a和b一定是先后进行出队的，顺序可以改变，但位置关系不能变，因此C选项是错误的；
• D选项中是以e为第一个出队元素，那么a和b一定是紧邻的，b和c一定是紧邻的，可以看到它的出队次序是没问题的；

因此这一题选C，下面我们就来通过画图验证一下结论，如下所示：

可以看到在C选项中不管c元素从哪端入队，都不可能在a和b的中间，因此C选项错误。

PS: 这里分享的经验纯属我个人的一个思考总结，不一定完全正确，所以希望大家在做题时可以通过画图法来验证一下答案是否正确。

总结

在今天的篇章中，我们详细的探讨了一下不同形态的双端队列以及双端队列的使用，并且今天还将我自己压箱底的经验分享了出来，希望能够帮助各位更好的理解双端队列以及它的使用，如果对于相关的知识点还有疑问的话可以在评论区进行提问，我会尽快给大家进行答疑的哦！

最后感谢大家的翻阅，咱们下一篇再见！！！