【论文阅读】HiNet Deep Image Hiding by Invertible Network

前言

• 博客主页：睡晚不猿序程
• ⌚首发时间：2022.8.8
• ⏰最近更新时间：2022.8.9
• 本文由 睡晚不猿序程 原创，首发于 CSDN
• 作者是蒻蒟本蒟，如果文章里有任何错误或者表述不清，请 tt 我，万分感谢！orz

---

相关文章目录 ：

• 【论文阅读】StegaStamp: Invisible Hyperlinks in Physical Photographs

---

1. 内容简介

本片博客将会一起阅读 HiNet: Deep Image Hiding by Invertible Network

论文标题：《HiNet: Deep Image Hiding by Invertible Network》

作者：Junpeng Jing，Xin Deng，Mai Xu，Jianyi Wang，Zhenyu Guan

发布于：ICCV 2021

自己认为的关键词：隐写术，图像隐藏

参考：csdn一位大佬的文章

---

2. 摘要浏览

隐写术的三个挑战：

1. 容量
2. 不可见性
3. 安全性

基于这三个挑战，该论文使用了一个基于可逆神经网络的框架，HiNet

对于大容量，本文采取了一种可逆的学习机制，他可以同时学习图像的隐藏和提取，HiNet可以做到把完全大小的秘密图像编码进入载体图像（和秘密图像的大小相同）

为了达到高度的不可见性，本文采取了把秘密图像编码进小波域，而不是像素域。

采取了低频小波域损失来约束模型把秘密信息写入图像的高频区域，这样可以显著的提升隐藏的安全性

实验结果：在多个通用图像数据集（ImageNet，COCO，DIV2K）上的图像隐写 SOTA

---

3. 图片、表格浏览

图 1

对比了HiNet和其他深度隐写技术的区别，一般的隐写系统会分别训练用来隐写的编码器网络和用来提取的解码器网络，而HiNet使用了类似可逆神经网络的结构，隐写和提取共享同一套参数

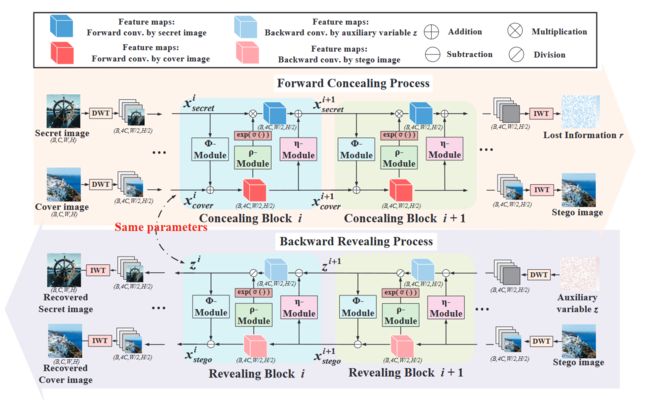
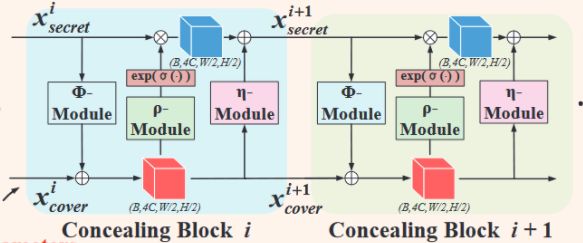
图 2

图 2 展示的是网络结构图以及编解码的步骤

表 1

文章中的符号信息

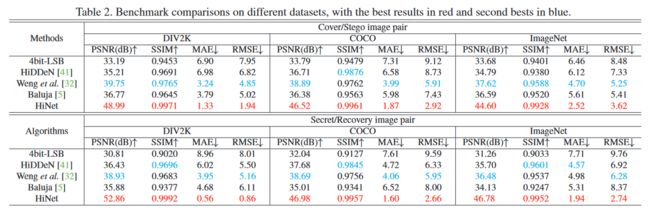
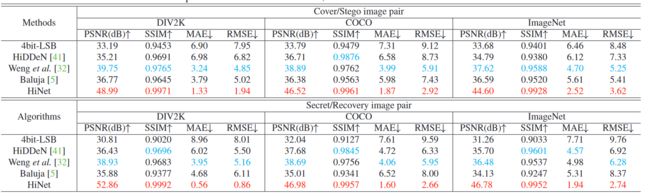
表 2

和其他 SOTA 模型的对比

可以看出实现的全面的超越和碾压

图 3

和以往的模型进行对比，可以看出其他模型在图像的平滑区域有伪影，但是该模型生成的几乎看不见伪影

图 4

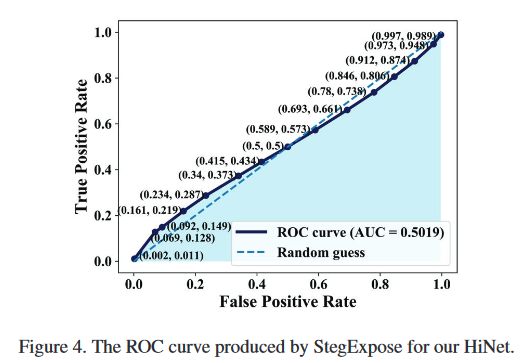使用 StegExpose 时 HiNet 的 ROC 曲线

参考资料：ROC曲线怎么看

所以曲线下方的面积越大，效果越好，这样看这个隐写分析算法的表现并不好，说明了 HiNet 应对隐写分析性能优越

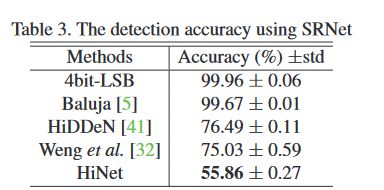
表 3

使用了 SRNet 作为隐写分析器，HiNet 的表现依然出色

图 5

不同隐写术抵抗隐写分析术的能力，可以看出 HiNet 的能力非常强大

表 4

用消融实验展示了在高频进行小波变换，也就是设置低频变换损失 $L_{freg}$ 的有效性

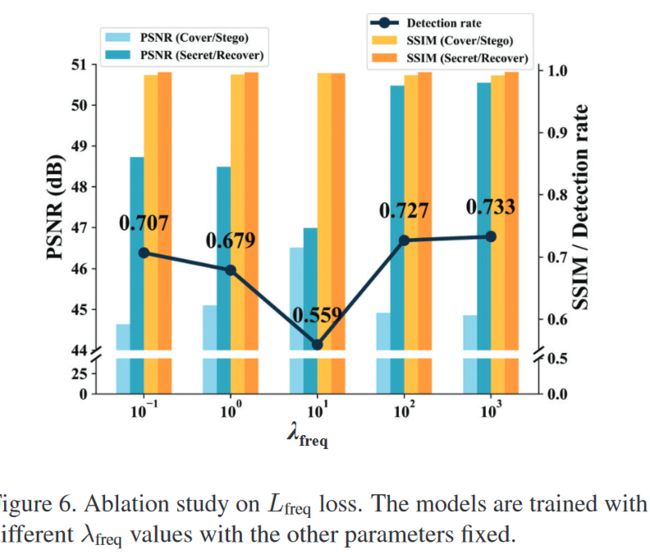
图 6

使用不同的 ${\lambda }_{freq}$的效果

图 7

用不同的架构来构建的效果

---

4. 引言浏览

图像隐藏的任务在于把秘密图像隐藏进一个载体图像中来生成隐写图像（stego image）

相较于比特级信息的隐藏，图片隐藏要求更大的容量，高不可见性和安全性

这里解释了图像隐藏和图像密码学的差异，图像隐藏更关注于容量和不可见性，而图像密码学更关注鲁棒性

Baluja提出了第一个CNN来解决图像隐藏的问题

Weng扩展了这一方法

但是传统方法都使用两套参数（编码器和解码器各用一套），二者是简单串联的，这种松散链接会导致色彩偏差和纹理复制伪影

本论文提出的 HiNet ，编解码采用的同一套参数

这是可逆神经网络第一次被应用到图像隐写的工作中，图像的编码和解码是通过同一套网络的，而且解码的过程就是编码的逆过程，这意味着网路只需要训练一次就可以得到所有参数，可以用于隐藏也可以用于解码

作者强调，该网络在恢复正确率，隐藏安全性和不可见度都实现了SOTA

贡献：

1. 提出了一个名为 HiNet 的图像隐藏网络，基于可逆神经网络，可用于大容量的图像隐藏
2. 设计了两个可微且可逆的隐藏和提取的模块，目的是让图片的隐藏过程完全可逆
3. 使用了低频小波损失来控制秘密信息在不同频带的分布，显著增强了隐藏的安全性

自由阅读

接下来是自由阅读时间，我阅读的顺序开始跳跃啦

---

5. 方法

首先输入的 Secret img 和 cover img 会进行 DWT 分解，然后被喂给一系列的隐藏模块，最后一个隐藏模块将会用一个 IWT（小波逆变换）生成 stego img 和损失信息 r

图像提取过程就是 stego img以及辅助变量 z 经过 DWT和一系列提取层最后恢复隐藏图像 secret img

5.1 小波域隐藏：

将信息隐藏进像素域容易导致伪影，隐藏进频域，特别是高频域对于图像隐藏更合适。

我们使用了 DWT 在图片进入网络前把图片分为高频域和低频域，这样网络将秘密信息融入cover img的效果更好

小波的优秀重构性质可以很好的降低信息损失，提升隐藏质量

我们使用了哈尔小波核来进行 DWT 和 IWT，经过 DWT，特征图的大小从(B,C,H,W)变为(B,4C,H/2,W/2)，且使用哈尔小波核，计算变得简单且高效

因为小波变换是双向对称的，所以对网络端到端的训练不会有影响

5.2 隐藏和提取块

隐藏和提取使用但是同一个网络参数，且使用同样的子模块，只不过是反过来了而已。每个模块都是一样的，输入是$x_{cover}$和$x_{secret}$，每个模块的输出依照以下的公式：
$$\begin{gathered} x_{cover}^{i+1}=x_{cover}^i+\varphi (x_{secret}^i) \\ {x}_{secret}^{i+1}=x_{secret}^i\odot exp(\alpha (\rho (x_{cover}^{i+1})))+\eta (x_{cover}^{i+1}) \end{gathered}$$
$\alpha$ ：是一个sigmoid函数乘以一个常数值？

$\odot$：代表点积运算

ρ(·)、φ(·) 和 η(·) 是任意函数，本文采用了ESRGAN中的 Dense block

上面三者使用不同的架构会有不同的效果，在后面几个章节我们有讨论

之后会对不同体系结构对这三个函数的影响进行讨论

经过了M个隐藏块，在最后一个隐藏模块之后，可以得到输出 $x_{cover}^{M+1}$ and $x_{secret}^{M+1}$ ，然后将输出送入两个 IWT 块，分别生成隐写图像 $x_{stego}$ 和丢失信息 $r$。

5.3 揭示模块

揭示过程中，信息流的方向是反过来的

具体来说，对于第 M 个揭示模块，输入是由隐写图像 $x_{stego}$ 和辅助变量 z 通过 DWT 生成的 $x^{M+1}_{stego} $and $z^{M+1} $ ，z是从高斯分布中随机抽样的，在最后一个揭示模块，即揭示模块 1 之后，输出 $x_{stego}^1$ 被送入 IWT 模块，生成恢复图像 $x_{rec}$。

其过程的公式如下：
$$\begin{gathered} {\mathbf{z}}^i=\left(z^{i+1}-\mathbf{\eta }\left(x_{\text{stego }}^{i+1}\right)\right)\odot \exp \left(-\alpha \left(\rho \left(x_{\text{stego }}^{i+1}\right)\right)\right) \\ {x}_{stego}^i=x_{stego}^{i+1}-\varphi (z^i) \end{gathered}$$
损失信息 r 和辅助变量 z

在隐藏过程中，网络试图将秘密图像隐藏到覆盖图像中。然而，如此大的容量很难隐藏在封面图像中，不可避免地导致秘密信息的丢失。另外，秘密图像的入侵可能会破坏封面图像中的原始信息。丢失的秘密信息和被破坏的掩护信息构成了丢失的信息 r。

但是，这里的丢失信息 r 被认为是个例无关的（case-notistic）

如何证明：

• 假设全部图像的分布为 $\chi$
• 训练过程中的图像全部图像都从中取样，所以$x_{cover},x_{secret}\sim \chi$
• 因为INN的可逆性，$x_{stego}$ 和 $r$ 也应该遵循相同分布
• $x_{stego}$ 和 $r$ 的混合分布也应遵循，例如$x_{stego}\times r\sim \chi$
• 因为隐藏图像$x_{stego}$ 和隐藏损失推动着$x_{stego}$ 去匹配分布 $\chi$ ，所以我们可以假设 r 是个例无关的

【大概意思就是说，这个损失 r 是和输入的图像无关的，不是输入一个图像就会输出一个特定的 r，这个 r 服从一个分布】

在恢复隐藏图像的过程中，只要求从隐写图像中提取，而不需要访问 r，这实际上是一个不适定的问题，因为可以从同一个 $x_{stego}$ 中恢复数百万个 $x_{rec}$.为了获得精确的 ，$x_{rec}$ 在反示过程中采用了一个辅助变量 $z$。

变量 z 是从一个个例无关分布中随机抽取的，该分布与 r 的分布相同。该分布是在训练时通过后面表示的揭示损失来学习的

z 的分布是通过揭示损失来学习的，他可以分布中的每一个样本都可以很好的复原秘密信息。如果不考虑损失，我们假设z服从一个高斯分布，比如 $z\sim N(u_0,{\sigma }_0^2)$

5.4 为什么 INN 可以用于图像隐藏？

文中提出了一种思想，图像隐藏任务有两个部分组成，一个部分是图像隐藏，另一个部分是图像提取

之前的想法是用两个前向网络来完成上面两个步骤，但是作者认为，要完成完美的隐藏，上面的两个部分要完全可逆（这算不算一种归纳偏置？）

基于此，作者把图像隐藏和图像提取作为了INN的前向和反向步骤

5.5 损失函数

三种损失共同组成损失函数

1. 隐藏损失：保证隐藏的质量
2. 提取损失：保证提取的质量
3. 【新】低频小波损失：迫使模型把信息隐藏到高频区域，提高隐写安全性

5.5.1 隐藏损失

$$L_{\mathrm{con}}(\mathbf{\theta })=\sum _{n=1}^N{\ell }_{\mathcal{C}}\left({\mathbf{x}}_{\text{cover }}^{(n)},{\mathbf{x}}_{\text{stego }}^{(n)}\right)$$

因为 $x_{stego}^{(n)}$等于 $f_{\theta }((x_{cover}^{(n)}),x_{stego}^{(n)})$ ，其中 $\theta$ 代表网络参数，N为训练样本量，${\ell }_{\mathcal{C}}$ 用来度量cover img 和 stego img 之间的不同，可以使用 L1 或者 L2 范数

5.5.2 提取损失

$$L_{\mathrm{rev}}(\mathbf{\theta })=\sum _{n=1}^N{\mathbb{E}}_{\mathbf{z}\sim p(\mathbf{z})}\left[{\ell }_{\mathcal{R}}\left({\mathbf{x}}_{\mathrm{secret}}^{(n)},{\mathbf{x}}_{\mathrm{rec}}^{(n)}\right)\right]$$

在反向穿过网络提取图像的时候，网络要能通过任意的样本 $z$ （z来自一个高斯分布 $p(z)$），所以我们构造了提取损失（如上）

${\ell }_{\mathcal{R}}$ 用来度量二者的不同，和上面的 ${\ell }_{\mathcal{C}}$ 类似

5.5.3 低频小波损失

$$L_{\mathrm{freq}}(\mathbf{\theta })=\sum _{n=1}^N{\ell }_{\mathcal{F}}\left(\mathcal{H}{\left({\mathbf{x}}_{\text{cover }}^{(n)}\right)}_{LL},\mathcal{H}{\left({\mathbf{x}}_{\text{stego }}^{(n)}\right)}_{LL}\right)$$

构造这个损失的灵感来源于【Shumeet Baluja. Hiding images in plain sight: Deep steganography. In Advances in Neural Information Processing Systems, pages】，因为秘密信息如果隐藏在高频部分相较于隐藏于低频部分更难被察觉到

为了让大部分信息都隐藏在高频子带上，我们要求经过小波分解后， stego img 的低频子带要和 cover img 的低频子带相似

$\mathcal{H}(\cdot {)}_{LL}$ 代表提取经过小波分解的低频子带

${\ell }_{\mathcal{F}}$ 用来度量二者的不同

5.5.4 总损失

$$L_{\text{total }}={\lambda }_c{L}_{\mathrm{con}}+{\lambda }_r{L}_{\mathrm{rev}}+{\lambda }_f{L}_{\mathrm{freq}}$$

总损失是上面三种损失的加权和，刚开始训练的时候，我们让 ${\lambda }_f$ 为0，接着我们再加入加入 $L_{freq}$ 来进行端到端的训练

---

6. 实验

6.1 实验环境配置

数据集 ：

训练集：

• DIV2K 的训练集

测试集：

• DIV2K 的测试集的100张图片，重采样为 1024*1024
• ImageNet 中的 50,000 张图片，重采样为 256*256
• COCO 中的 5,000 张图片，重采样为 256*256

【注】使用中心裁切

使用的隐写模块和提取模块数M为16

用于训练的图像大小为 256*256

共训练 80K 次${\lambda }_c,{\lambda }_r,{\lambda }_f$ 分别为10.0，1.0，10.0

mini-batch 大小为16，其中随机取一半作为 cover img，另一半作为 secret img

使用 Adam 优化器，学习率 1e-4.5，每10K个iterations 减半

基准

对比了多个方法

1. 4bit-LSB
2. HiDDeN
3. Wenget al方法
4. Baluja

对上面三种神经网络的方法进行了重新训练，使用了一样的训练集

原本的 HiDDeN 网络只能隐藏信息，所以我们重构了他的输出维度让他可以解码图片，并重新进行训练

评价指标

评价 cover/stego ，secret/recovery 之间的质量

使用 PSNR 和 SSIM 以及 MAE 进行评价

PSNR 和 SSIM 越大越好，MAE 越小越好

并且使用了两个隐写分析工具来验证安全性：

• StegExpose
• SRNet

这个表格展示了他的性能，实现全面超越啊

6.2 模块对比

作者使用了 convolutional block，residual block，dense block，然后对比了他们的 PSNR，发现 dense block 是最好的

---

附 训练

尝试了一下他的训练过程

我采用了 DIV2K数据集进行训练

在colab上使用 P100（开了一个月会员，肉疼），batch_szie=8，训练了100个epoch

训练效果都不错

---

7. 总结、预告

感觉这篇文章的作者太强了，可以实现这么复杂的网络（在我认为），而且仅是随意的训练一小段时间就能达到很不错的效果，真的好厉害

下一篇打算看下这位大佬作者今年的新论文了，名字是 DeepMIH: Deep Invertible Network for Multiple Image Hiding，发表在 TPAMI，真的太强啦！！！