数据结构 - 堆的应用场景
目录
1、优先级队列的使用场景
1)、定时任务轮训问题
2)、合并有序小文件
2、求Top K值问题【使用一个堆解决】
3、求中位数、百分位数【使用一个大顶堆一个小顶堆解决】
4、大数据量日志统计搜索排行榜【散列表+堆】
堆作为数据结构其本身是完全二叉树(即满足完全二叉树的特性),作为数据特点堆顶元素大于等于(或者小于等于)索引叶子节点。前面篇博客分析了,堆排序也算是堆的一个应用场景,并且分析了堆排序的第一步建堆,允许在时间复杂度O(N)内就获取到了最大或者最小的元素【而我们使用排序的思想,那么快排等时间复杂度最低也是O(N*logN)】。Java中的PriorityQueue(优先级队列)本身就是数据结构堆,所以基于优先级队列的所有应用场景,都是数据结构堆的应该场景。所以堆集上面的所有特点于一身,定有自己非常多的使用场景,并且个人理解:只有对一种数据结构、设计模式等事物有一定的认识,当在纷乱的需求中才能梳理使用在合适的位置;其次穷举每种特性的使用场景,也能更好的反哺理解。
下面整理了几种堆的常用场景:
1、优先级队列的使用场景
1)、定时任务轮训问题
定时任务或者分布式定时任务的场景我们都开发过,用户(开发或者运营)可以在页面操作,添加或修改定时任务的执行时间,当然一般会使用cron表达式进行配置【我们可以解析成具体的时间】。或者自己之前做商品系统时,里面有一个打标的开始和结束时间,怎么才能让开始时间去做一些事,结束时间到了再触发做一些事呢?
没错我们使用的就是轮训的方式,两个定时任务专门扫描开始和结束时间,按照时间倒排序,找到需要触发的数据。轮训扫描需要有执行的间隔机制,如果扫描太频繁会影响性能,如果扫描时间间隔太大,扫描时发现本来应该是5分钟之前触发执行的数据,只有到了扫描间隔才知道。 所以两个弊病就是 浪费资源(可能1天后执行的任务,被扫描多次)、执行不及时(本来上次扫描完过几秒钟就该执行的)。
这样的场景其实就可以使用一个小顶堆进行处理,先扫描一次将所有数据都添加到小顶堆中,堆顶元素就是最先会被执行的任务。那么在堆顶任务执行之前其他任务肯定不可能执行。获取堆顶任务,到点执行的同时,【可以并行】再来获取下一个堆顶元素,数据结构 - 堆中我们知道,当获取了堆顶元素后,堆内部会再执行从上往下的堆化操作,获取次小元素放在堆顶。
2)、合并有序小文件
有1000个小文件中存储了有序的字符串信息,我们需要将所有的有序小文件合并成一个大文件。比如 文件3.txt存储了【123,...555】 ,文件 8.txt 存储了 【556,... ,888】,最终需要将所有文件合并成整体有序文件。
此时我们就可以创建一个堆,遍历所有小文件,都获取第一行数据添加到小顶堆中。比如Java的PriorityQueue
2、求Top K值问题【使用一个堆解决】
Top k值问题是堆的最典型的应该场景,也是面试高频,对应LeetCode 703。如已经有一堆统计数据,字符串aaa出现了3次,字符串bbb出现了99次,,,。最后想统计出现次数最多的5种字符串,或者出现第5多的字符串。
这种场景我们直接维护一个堆大小为5的小顶堆【堆顶元素就是第5大值】,当长度不满5时直接添加到小顶堆中。否则需要查看堆顶元素的次数是否小于要添加的字符串的次数,如果是则用当前值替换堆顶元素,再从上往下进行堆化,新的堆顶元素就是第5大元素。重复这样的动作,最后拿到的堆顶就是第5大的元素; 如果同时还想获取排序后的Top5值,前面的动作类比堆排序的第一步建堆操作,我们只需要将该堆执行时间复杂度为O(N*logN)的排序操作即可(可以参见上一篇博客:排序算法 - 堆排序)。
/**
* 流数据中的第K大元素
*
* 1、每次给元素进行排序,可以考虑使用快排,那么时间复杂的也是 K*logK
* 2、创建一个长度为K的小顶堆(java的{@link PriorityQueue} 使用的是严格的斐波那契堆,性能非常的高
* 第k大的元素永远在堆顶) 那么时间复杂都为 log2K
*
* @author kevin
* @date 2021/2/15 22:50
* @since 1.0.0
*/
public class KthLargest703 {
public static void main(String[] args) {
int[] init = new int[]{4, 5, 8, 2};
KthLargest703 kthLargest = new KthLargest703(3, init);
System.out.println("return 4 --> " + kthLargest.add(3)); // return 4
System.out.println("return 5 --> " + kthLargest.add(5)); // return 5
System.out.println("return 5 --> " + kthLargest.add(10)); // return 5
System.out.println("return 8 --> " + kthLargest.add(9)); // return 8
System.out.println("return 8 --> " + kthLargest.add(4)); // return 8
}
private PriorityQueue priorityQueue;
private int k;
public KthLargest703(int k, int[] numArray) {
this.k = k;
priorityQueue = new PriorityQueue<>(k);
for (int num : numArray) {
add(num);
}
}
public int add(int val) {
if (priorityQueue.size() < k) {
priorityQueue.offer(val);
} else if (priorityQueue.peek() < val) {
// 新添加的值比栈顶元素大,则移除该小顶堆的top,再添加新的元素
priorityQueue.poll();
priorityQueue.offer(val);
}
return priorityQueue.peek();
}
} 3、求中位数、百分位数【使用一个大顶堆一个小顶堆解决】
求中位数和求百分位数是一样的场景,只是具体计算、调整大顶堆和小顶堆大小时不同。这样的场景比如出现在压测的场景,Jemeter压测前需要先预定聚合报告,自己是想统计中位数,80%位置,或者类似上面的Tp 9999的接口性能耗时。
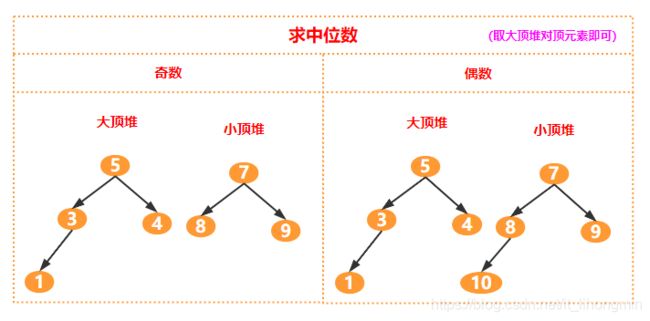
先分析中位数,那么有两种情况压测前不知道会压测多少次,比如执行压测5分钟;还有一种情况就是压测1000次。最后总次数是可知的,那么中位数为总次数的一半,可以将中位数分为奇数和偶数两种情况,那么可以使用两个堆,如下图:
中位数:
静态数据:静态数据本身已经知道的中位的值,比如长度为N,那么中位值为N/2,可以转换为上面的Top N/2的问题,也可以基于下面的流式计算中位值处理。
流式数据:维护一个大顶堆和一个小顶堆,用一个int记录两个堆的元素总和,添加一个数据时候先取大顶堆的堆顶元素判断,如果当前值小于堆顶元素则添加到小顶堆(否则添加到大顶堆)。再判断小顶堆个数是否满足 N/2或者 N/2 + 1,如果是添加到了
大顶堆则判断是否满足大顶堆的个数永远为 N/2;如果不满足则从该堆顶取一个元素添加到另一个堆。
百分位数:计算方式如上面的流式计算,只是判断时, 如果百分80位置 则小顶堆个数永远维护为 N*80%个。
4、大数据量日志统计搜索排行榜【散列表+堆】
有10亿(或者50G)的查询关键词,需要进行排序求Top K,类似在搜索引擎框中提示。分为两种情况,看能否一次性加载到内存中:
可以一次性加载到内存中:
可以基于散列表读写的时间复杂度近似O(1),统计每个搜索词出现的次数,再使用堆或者优先级队列 处理类似上面 TopK的思路(也是堆化的过程),最后再进行堆排序就是想要的排序结果。
不能一次性加载到内存中:
使用Hash算法将大文件散列到多个(根据预计算得出,比如10亿条数据,平均每条多大,总共多大数据,每次可以加载多少道内存中处理)文件中, 为了防止TopK的数据都退化到一个子文件中,所以每个子文件都要获取前TopK的值,最后将所有值进行合并,就得到了最后的 TopK。