堆（数据结构）

1.堆的概念

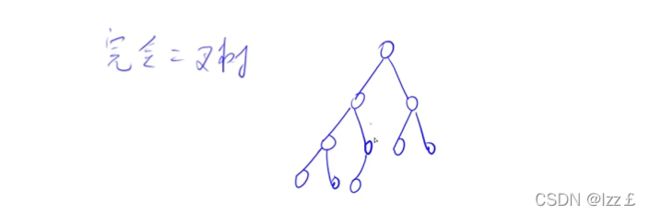
如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<=K2i+2 ，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。完全二叉树（除了最后一层以外上面的节点但是非空的，最后一层节点是从左到右依次排布的）。如图：

2.堆的性质

1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。

2.堆的存储

   堆的存储不同于链表的存储，堆的存储是用一个一维数组来存储的。以小根堆为例，根节点为最小值，小于它的左儿子和右儿子。根节点x存储在小标为1的数组里，左儿子存储在下标为2x的数组，右儿子存储在下标为2x+1的数组里。

3.堆的基本操作（小根堆为例）

   堆的两个基本操作为down操作和up操作，顾名思义，down操作就是向下调整，up操作就是向上调整，这两个操作即可以完成以上的五个问题。

     down操作如图所示移动，因为我将根节点或者某一点改变后，这一点比它的儿子点大了，所以我们要将这个点向下移动，直到重新成为一个堆。

   up操作，和down操作相反，up操作是将一个点的值变小，然后不断向上移动直到成为一个新的堆。同样如图：

 4.如何手写一个堆（小根堆）

     1）插入一个数：插入一个数是在数组的最后面插入,然后不断往上移，heap[++size]=x，up(size)；

     2）求集合中的最小值：数组第一个数一定是最小的；heap[1];

     3）删除最小值:  删除最小值需要一定技巧，因为堆是一个一维数组，删除第一个比较困难，所以将数组的最后一个覆盖到第一个数，然后将最后一个数删除，最后在down操作一遍；heap[1]=heap[size],size--,down(1);

     4）删除任何一个元素: 和删除根节点是类似的，假如是第k的点那么就是让最后一个数等于第k个数，这里需要判断一下看看改变后的k是变大了还是变小了，我们也可以不进行判断直接down操作一遍up操作一遍，因为无外乎只有3种情况变大，变小或者不变，所以down和up只会选择一个。heap[k]=heap[size],size--,down(k),up(k);

     5）修改任何一个元素: 修改一个元素和删除一个元素同理，我们修改完以后down操作一遍up操作一遍就可以了。heap[k]=x,down(k),up(k);

5.堆的模板

  down模板：

#include
using namespace std;
const int N=100010;
int h[N],siz;
int n,m;
void down(int x)
{
    int t=x;
    if(2*x<=siz && h[2*x]     if(2*x+1<=siz && h[2*x+1]     if(x!=t)
    {
        swap(h[x],h[t]);
        down(t);
    }
}

up模板：

void up(int x)
{
    while(x/2 &&h[x]     {
        headswap(x/2,x);
        x/=2;
    }

 6.数据结构中堆和栈的不同

堆和栈在数据结构中是两种不同的数据结构。 两者都是数据项按序排列的数据结构。

   栈：像是装数据的桶或者箱子

 栈是大家比较熟悉的一种数据结构，它是一种具有后进先出的数据结构，也就是说后存放的先取，先存放的后取，这就类似于我们要在取放在箱子底部的东西（放进去比较早的物体），我们首先要移开压在它上面的物体（放入比较晚的物体）。

   堆：像是一颗倒立的大树

   堆是一种经过排序的树形数据结构，每个节点都有一个值。通常我们所说的堆的数据结构是指二叉树。堆的特点是根节点的值最小（或最大），且根节点的两个树也是一个堆。由于堆的这个特性，常用来实现优先队列，堆的存取是随意的，这就如同我们在图书馆的书架上取书，虽然书的摆放是有顺序的，但是我们想取任意一本时不必像栈一样，先取出前面所有的书，书架这种机制不同于箱子，我们可以直接取出我们想要的书。