AtCoder Beginner Contest 338（ABCDEF题）

A - Capitalized?

Problem Statement

You are given a non-empty string $S$ consisting of uppercase and lowercase English letters. Determine whether the following condition is satisfied:
The first character of $S$ is uppercase, and all other characters are lowercase.

Constraints

$1\le |S|\le 100$ ($|S|$ is the length of the string $S$.)
Each character of $S$ is an uppercase or lowercase English letter.

Input

The input is given from Standard Input in the following format:

$S$

Output

If the condition is satisfied, print Yes; otherwise, print No.

Sample Input 1

Capitalized

Sample Output 1

Yes

The first character C of Capitalized is uppercase, and all other characters apitalized are lowercase, so you should print Yes.

Sample Input 2

AtCoder

Sample Output 2

No

AtCoder contains an uppercase letter C that is not at the beginning, so you should print No.

Sample Input 3

yes

Sample Output 3

No

The first character y of yes is not uppercase, so you should print No.

Sample Input 4

A

Sample Output 4

Yes

Solution

具体见文末视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	string S;

	cin >> S;

	int Cnt = 0;
	for (auto c : S)
		if (isupper(c))
			Cnt ++;

	if (Cnt == 1 && isupper(S[0])) cout << "Yes" << endl;
	else cout << "No" << endl;

	return 0;
}

B - Frequency

Problem Statement

You are given a string $S$ consisting of lowercase English letters. Find the character that appears most frequently in $S$. If multiple such characters exist, report the one that comes earliest in alphabetical order.

Constraints

$1\le |S|\le 1000$ ($|S|$ is the length of the string $S$.)
Each character in $S$ is a lowercase English letter.

Input

The input is given from Standard Input in the following format:

$S$

Output

Among the characters that appear most frequently in $S$, print the one that comes earliest in alphabetical order.

Sample Input 1

frequency

Sample Output 1

e

In frequency, the letter e appears twice, which is more than any other character, so you should print e.

Sample Input 2

atcoder

Sample Output 2

a

In atcoder, each of the letters a, t, c, o, d, e, and r appears once, so you should print the earliest in alphabetical order, which is a.

Sample Input 3

pseudopseudohypoparathyroidism

Sample Output 3

o

Solution

具体见文末视频。

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	string S;
	int Cnt[27] = {0};

	cin >> S;

	for (auto c : S)
		Cnt[c - 'a'] ++;

	int Max = -1, P;
	for (int i = 0; i < 26; i ++)
		if (Cnt[i] > Max)
			Max = Cnt[i], P = i;

	cout << char(P + 'a') << endl;

	return 0;
}

C - Leftover Recipes

Problem Statement

Your refrigerator has $N$ kinds of ingredients. Let us call them ingredient $1$, $\dots$, ingredient $N$. You have $Q_i$ grams of ingredient $i$.
You can make two types of dishes. To make one serving of dish A, you need $A_i$ grams of each ingredient $i$ $(1\le i\le N)$. To make one serving of dish B, you need $B_i$ grams of each ingredient $i$. You can only make an integer number of servings of each type of dish.
Using only the ingredients in the refrigerator, what is the maximum total number of servings of dishes you can make?

Constraints

$1\le N\le 10$
$1\le Q_i\le 10^6$
$0\le A_i\le 10^6$
There is an $i$ such that $A_i\ge 1$.
$0\le B_i\le 10^6$
There is an $i$ such that $B_i\ge 1$.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$Q_1$ $Q_2$ $\dots$ $Q_N$
$A_1$ $A_2$ $\dots$ $A_N$
$B_1$ $B_2$ $\dots$ $B_N$

Output

Assuming that you can make a maximum total of $S$ servings of dishes, print the integer $S$.

Sample Input 1

2
800 300
100 100
200 10

Sample Output 1

5

This refrigerator has $800$ grams of ingredient $1$ and $300$ grams of ingredient $2$.
You can make one serving of dish A with $100$ grams of ingredient $1$ and $100$ grams of ingredient $2$, and one serving of dish B with $200$ grams of ingredient $1$ and $10$ grams of ingredient $2$.
To make two servings of dish A and three servings of dish B, you need $100\times 2+200\times 3=800$ grams of ingredient $1$, and $100\times 2+10\times 3=230$ grams of ingredient $2$, neither of which exceeds the amount available in the refrigerator. In this way, you can make a total of five servings of dishes, but there is no way to make six, so the answer is $5$.

Sample Input 2

2
800 300
100 0
0 10

Sample Output 2

38

You can make $8$ servings of dish A with $800$ grams of ingredient $1$, and $30$ servings of dish B with $300$ grams of ingredient $2$, for a total of $38$ servings.

Sample Input 3

2
800 300
801 300
800 301

Sample Output 3

0

You cannot make any dishes.

Sample Input 4

10
1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000
0 1 2 3 4 5 6 7 8 9
9 8 7 6 5 4 3 2 1 0

Sample Output 4

222222

Solution

具体见文末视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 20;

int N;
int Q[SIZE], A[SIZE], B[SIZE];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N;

	int Min = 1e18;
	for (int i = 1; i <= N; i ++)
		cin >> Q[i];
	for (int i = 1; i <= N; i ++)
		cin >> A[i], Min = min(Min, A[i] == 0 ? (int)1e18 : Q[i] / A[i]);
	for (int i = 1; i <= N; i ++)
		cin >> B[i];

	int Result = 0;
	for (int i = 0; i <= Min; i ++)
	{
		int Min = 1e18;
		for (int j = 1; j <= N; j ++)
			Min = min(Min, B[j] == 0 ? (int)1e18 : (Q[j] - i * A[j]) / B[j]);
		Result = max(Result, Min + i);
	}

	cout << Result << endl;

	return 0;
}

D - Island Tour

Problem Statement

The AtCoder Archipelago consists of $N$ islands connected by $N$ bridges.
The islands are numbered from $1$ to $N$, and the $i$-th bridge ($1\le i\le N-1$) connects islands $i$ and $i+1$ bidirectionally, while the $N$-th bridge connects islands $N$ and $1$ bidirectionally.
There is no way to travel between islands other than crossing the bridges.
On the islands, a tour that starts from island $X_1$ and visits islands $X_2,X_3,\dots ,X_M$ in order is regularly conducted.
The tour may pass through islands other than those being visited, and the total number of times bridges are crossed during the tour is defined as the length of the tour.
More precisely, a tour is a sequence of $l+1$ islands $a_0,a_1,\dots ,a_l$ that satisfies all the following conditions, and its length is defined as $l$:
For all $j(0\le j\le l-1)$, islands $a_j$ and $a_{j+1}$ are directly connected by a bridge.
There are some KaTeX parse error: Expected 'EOF', got '&' at position 9: 0 = y_1 &̲lt; y_2 < \d… such that for all $k(1\le k\le M)$, $a_{y_k}=X_k$.
Due to financial difficulties, the islands will close one bridge to reduce maintenance costs.
Determine the minimum possible length of the tour when the bridge to be closed is chosen optimally.

Constraints

$3\le N\le 2\times 10^5$
$2\le M\le 2\times 10^5$
$1\le X_k\le N$
$X_k\ne X_{k+1}(1\le k\le M-1)$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$X_1$ $X_2$ $\dots$ $X_M$

Output

Print the answer as an integer.

Sample Input 1

3 3
1 3 2

Sample Output 1

2

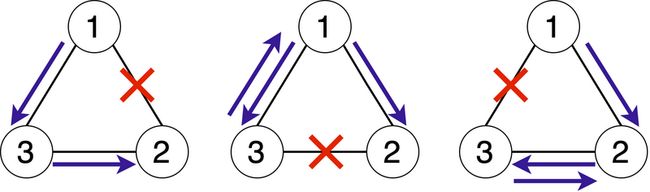
If the first bridge is closed: By taking the sequence of islands $(a_0,a_1,a_2)=(1,3,2)$, it is possible to visit islands $1,3,2$ in order, and a tour of length $2$ can be conducted. There is no shorter tour.
If the second bridge is closed: By taking the sequence of islands $(a_0,a_1,a_2,a_3)=(1,3,1,2)$, it is possible to visit islands $1,3,2$ in order, and a tour of length $3$ can be conducted. There is no shorter tour.
If the third bridge is closed: By taking the sequence of islands $(a_0,a_1,a_2,a_3)=(1,2,3,2)$, it is possible to visit islands $1,3,2$ in order, and a tour of length $3$ can be conducted. There is no shorter tour.
Therefore, the minimum possible length of the tour when the bridge to be closed is chosen optimally is $2$.
The following figure shows, from left to right, the cases when bridges $1,2,3$ are closed, respectively. The circles with numbers represent islands, the lines connecting the circles represent bridges, and the blue arrows represent the shortest tour routes.

Sample Input 2

4 5
2 4 2 4 2

Sample Output 2

8

The same island may appear multiple times in $X_1,X_2,\dots ,X_M$.

Sample Input 3

163054 10
62874 19143 77750 111403 29327 56303 6659 18896 64175 26369

Sample Output 3

390009

Solution

具体见文末视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 2e5 + 10;

int N, M;
int X[SIZE];
std::vector<int> L[SIZE], R[SIZE];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> M;

	for (int i = 1; i <= M; i ++)
		cin >> X[i];

	for (int i = 2; i <= M; i ++)
		L[X[i - 1]].push_back(X[i]), R[X[i]].push_back(X[i - 1]);

	int Result = 0;
	for (int i = 1; i <= N; i ++)
		for (auto j : L[i])
			Result += abs(j - i);

	int Last = N, Tmp = Result;
	for (int i = 1; i < N; i ++)
	{
		for (auto j : L[Last])
		{
			int A = (j + i - 1) % N, B = (Last + i - 1) % N;
			if (!A) A = N;
			if (!B) B = N;
			int A2 = (A + 1) % N, B2 = (B + 1) % N;
			if (!A2) A2 = N;
			if (!B2) B2 = N;
			Tmp -= abs(A - B), Tmp += abs(A2 - B2);
		}
		for (auto j : R[Last])
		{
			int A = (j + i - 1) % N, B = (Last + i - 1) % N;
			if (!A) A = N;
			if (!B) B = N;
			int A2 = (A + 1) % N, B2 = (B + 1) % N;
			if (!A2) A2 = N;
			if (!B2) B2 = N;
			Tmp -= abs(A - B), Tmp += abs(A2 - B2);
		}
		Result = min(Result, Tmp);
		Last --;
	}

	cout << Result << endl;

	return 0;
}

E - Chords

Problem Statement

There are $2N$ points placed at equal intervals on a circle, numbered $1$ to $2N$ in a clockwise direction starting from a certain point.
There are also $N$ chords on the circle, with the $i$-th chord connecting points $A_i$ and $B_i$.
It is guaranteed that all the values $A_1,\dots ,A_N,B_1,\dots ,B_N$ are distinct.
Determine whether there is an intersection between the chords.

Constraints

$2\le N\le 2\times 10^5$
$1\le A_i,B_i\le 2N$
$A_1,\dots ,A_N,B_1,\dots ,B_N$ are all distinct
All input values are integers

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $B_1$
$A_2$ $B_2$
$⋮$
$A_N$ $B_N$

Output

If there is an intersection between the chords, print Yes; otherwise, print No.

Sample Input 1

3
1 3
4 2
5 6

Sample Output 1

Yes

As shown in the figure, chord $1$ (the line segment connecting points $1$ and $3$) and chord $2$ (the line segment connecting points $4$ and $2$) intersect, so print Yes. ## Sample Input 2 ``` 3 6 1 4 3 2 5 ``` ## Sample Output 2 ``` No ``` As shown in the figure, there is no intersection between the chords, so print No. ## Sample Input 3 ``` 4 2 4 3 7 8 6 5 1 ``` ## Sample Output 3 ``` Yes ```

Solution

具体见文末视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 4e5 + 10;

int N;
int A[SIZE], B[SIZE];
PII Seg[SIZE];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N;

	for (int i = 1; i <= N; i ++)
	{
		cin >> A[i] >> B[i];
		if (A[i] > B[i]) swap(A[i], B[i]);
		Seg[i] = {A[i], B[i]};
	}

	sort(Seg + 1, Seg + 1 + N);

	set<int> R;
	R.insert(Seg[1].second);
	for (int i = 2; i <= N; i ++)
	{
		auto it = R.upper_bound(Seg[i].first);
		if (it == R.end())
		{
			R.insert(Seg[i].second);
			continue;
		}
		if ((*it) < Seg[i].second)
		{
			cout << "Yes" << endl;
			return 0;
		}
		R.insert(Seg[i].second);
	}

	cout << "No" << endl;

	return 0;
}

F - Negative Traveling Salesman

Problem Statement

There is a weighted simple directed graph with $N$ vertices and $M$ edges.
The vertices are numbered $1$ to $N$, and the $i$-th edge has a weight of $W_i$ and extends from vertex $U_i$ to vertex $V_i$.
The weights can be negative, but the graph does not contain negative cycles.
Determine whether there is a walk that visits each vertex at least once. If such a walk exists, find the minimum total weight of the edges traversed.
If the same edge is traversed multiple times, the weight of that edge is added for each traversal.
Here, “a walk that visits each vertex at least once” is a sequence of vertices $v_1,v_2,\dots ,v_k$ that satisfies both of the following conditions:
For every $i$ $(1\le i\le k-1)$, there is an edge extending from vertex $v_i$ to vertex $v_{i+1}$.
For every $j(1\le j\le N)$, there is $i$ $(1\le i\le k)$ such that $v_i=j$.

Constraints

$2\le N\le 20$
$1\le M\le N(N-1)$
$1\le U_i,V_i\le N$
$U_i\ne V_i$
$(U_i,V_i)\ne (U_j,V_j)$ for $i\ne j$
$-10^6\le W_i\le 10^6$
The given graph does not contain negative cycles.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$U_1$ $V_1$ $W_1$
$U_2$ $V_2$ $W_2$
$⋮$
$U_M$ $V_M$ $W_M$

Output

If there is a walk that visits each vertex at least once, print the minimum total weight of the edges traversed. Otherwise, print No.

Sample Input 1

3 4
1 2 5
2 1 -3
2 3 -4
3 1 100

Sample Output 1

-2

By following the vertices in the order $2\to 1\to 2\to 3$, you can visit all vertices at least once, and the total weight of the edges traversed is $(-3)+5+(-4)=-2$.
This is the minimum.

Sample Input 2

3 2
1 2 0
2 1 0

Sample Output 2

No

There is no walk that visits all vertices at least once.

Sample Input 3

5 9
1 2 -246288
4 5 -222742
3 1 246288
3 4 947824
5 2 -178721
4 3 -947824
5 4 756570
2 5 707902
5 1 36781

Sample Output 3

-449429

Solution

具体见文末视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 21;

int N, M;
int D[SIZE][SIZE];
int F[SIZE][1 << SIZE];

void Floyd()
{
    for (int k = 1; k <= N; k ++)
        for (int i = 1; i <= N; i ++)
            for (int j = 1; j <= N; j ++)
                D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> M;

	memset(D, 0x3f, sizeof D);
	int u, v, w;
	for (int i = 1; i <= M; i ++)
		cin >> u >> v >> w, D[u][v] = w;
	for (int i = 1; i <= N; i ++)
		D[i][i] = 0;

	Floyd();

	memset(F, 0x3f, sizeof F);
	for (int i = 1; i <= N; i ++)
		F[i][1 << i - 1] = 0;
	for (int i = 1; i < 1 << N; i ++)
		for (int j = 1; j <= N; j ++)
			if ((i >> j - 1) & 1)
				for (int k = 1; k <= N; k ++)
					if (!((i >> k - 1) & 1))
						F[k][i | (1 << k - 1)] = min(F[k][i | (1 << k - 1)], F[j][i] + D[j][k]);

	int Result = 1e18;
	for (int i = 1; i <= N; i ++)
		Result = min(Result, F[i][(1 << N) - 1]);

	if (Result == 1e18) cout << "No" << endl;
	else cout << Result << endl;

	return 0;
}

视频题解

Atcoder Beginner Contest 338

---

最后祝大家早日