【LeetCode】排序精选12题
目录
排序:
1. 合并区间(中等)
2. 数组的相对排序(简单)
快速排序:
1. 颜色分类(中等)
2. 排序数组(中等)
3. 数组中的第K个最大元素(中等)
4. 最小K个数(中等)
归并排序:
1. 排序数组(中等)
2. 交易逆序对的总数(困难)
3. 计算右侧小于当前元素的个数(困难)
4. 翻转对(困难)
5. 排序链表(中等)
6. 合并 K 个升序链表(困难)
6.1 递归解法(归并)
6.2 迭代解法(堆)
排序:
1. 合并区间(中等)
先将所有区间按照起始位置排序。如果当前区间的起始位置 <= 前一个区间的结束位置,则可以合并,前一个区间不变,当前区间变为合并后的区间。如果当前区间和前一个区间不能合并,则把前一个区间加到答案中。遍历完成后,还要把最后一个区间加到答案中。
class Solution {
public:
vector> merge(vector>& intervals) {
int n = intervals.size();
sort(intervals.begin(), intervals.end());
vector> ans;
for (int i = 1; i < n; i++)
{
if (intervals[i][0] <= intervals[i - 1][1])
{
// 合并
intervals[i][0] = min(intervals[i][0], intervals[i - 1][0]);
intervals[i][1] = max(intervals[i][1], intervals[i - 1][1]);
}
else
{
ans.push_back(intervals[i - 1]);
}
}
ans.push_back(intervals[n - 1]);
return ans;
}
}; 2. 数组的相对排序(简单)
对于arr1的两个元素:
- 如果都在arr2中,按下标进行比较,下标小的靠前
- 如果一个在arr2中,一个不在arr2中,在arr2中的靠前
- 如果都不在arr2中,直接比较两个元素的大小即可
使用哈希表记录arr2中的元素,key——arr2中的某元素,value——该元素对应的下标。
使用sort函数搭配lambda表达式实现自定义排序。
class Solution {
public:
vector relativeSortArray(vector& arr1, vector& arr2) {
unordered_map hash;
// 初始化哈希表
for (int i = 0; i < arr2.size(); i++)
{
hash[arr2[i]] = i;
}
// 自定义排序
sort(arr1.begin(), arr1.end(), [&](int e1, int e2)
{
if (hash.count(e1) && hash.count(e2))
return hash[e1] < hash[e2];
else if (hash.count(e1))
return true;
else if (hash.count(e2))
return false;
else
return e1 < e2;
});
return arr1;
}
}; 快速排序:
1. 颜色分类(中等)
类比移动零:
![]()
得出数组分三块的示意图:
- left指向0序列的最后一个,因此初始化为-1
- i用来扫描数组,因此初始化为0
- right指向2序列的第一个,因此初始化为n
class Solution {
public:
void sortColors(vector& nums) {
int n = nums.size();
int left = -1;
int right = n;
int i = 0;
while (i < right)
{
if (nums[i] == 0)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] == 1)
{
i++;
}
else
{
swap(nums[--right], nums[i]);
}
}
}
}; 2. 排序数组(中等)
普通快排会超时,必须优化,可以使用数组划分三块的思想搭配随机选择基准元素的方法。
在待排序表中随机取一个元素key作为基准值,通过一趟排序将待排序表划分为独立的三部分区间[0, left],区间[left + 1, right - 1],区间[right, n - 1],使得区间[0, left]中的所有元素小于key,区间[left + 1, right - 1]中的所有元素等于key,区间[right, n - 1]中的所有元素大于key,则等于key的元素都放在了其最终位置——区间[left + 1, right - 1]上,这个过程称为一次划分。然后分别递归地对两个没排好序的子表重复上述过程,直至每部分内只有一个元素或空为止,即所有元素放在了其最终位置上。
class Solution {
public:
vector sortArray(vector& nums) {
srand((unsigned int)time(nullptr)); // 设置随机数种子
quickSort(nums, 0, nums.size() - 1);
return nums;
}
private:
void quickSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return;
// 划分左中右三个子区间
vector ret = partition(nums, begin, end);
int left = ret[0];
int right = ret[1];
// 递归排序左右两个子区间
quickSort(nums, begin, left);
quickSort(nums, right, end);
}
vector partition(vector& nums, int begin, int end)
{
// 随机取key
int key = nums[rand() % (end - begin + 1) + begin];
// 数组分三块
int left = begin - 1;
int right = end + 1;
int i = begin;
while (i < right)
{
if (nums[i] < key)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] == key)
{
i++;
}
else
{
swap(nums[--right], nums[i]);
}
}
return { left,right };
}
}; 3. 数组中的第K个最大元素(中等)
快速选择算法是基于快速排序算法思想的用于解决Top-K问题的算法,时间复杂度为O(n)。
在快排中,当我们把数组分成三块之后:[begin, left],[left + 1, right - 1],[right, end],我们可以通过计算每一个区间内元素的个数,进而推断出我们要找的元素是在哪一个区间里面。
class Solution {
public:
int findKthLargest(vector& nums, int k) {
srand((unsigned int)time(nullptr)); // 设置随机数种子
return quickSelect(nums, 0, nums.size() - 1, k);
}
private:
int quickSelect(vector& nums, int begin, int end, int k)
{
// 递归出口
if (begin == end)
return nums[begin];
// 划分左中右三个子区间
vector ret = partition(nums, begin, end);
int left = ret[0];
int right = ret[1];
int key = ret[2];
// 分类讨论
int c = end - right + 1;
int b = right - left - 1;
if (c >= k)
return quickSelect(nums, right, end, k);
else if (b + c >= k)
return key;
else
return quickSelect(nums, begin, left, k - b - c);
}
vector partition(vector& nums, int begin, int end)
{
// 随机取key
int key = nums[rand() % (end - begin + 1) + begin];
// 数组分三块
int left = begin - 1;
int right = end + 1;
int i = begin;
while (i < right)
{
if (nums[i] < key)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] == key)
{
i++;
}
else
{
swap(nums[--right], nums[i]);
}
}
return { left,right,key };
}
}; 4. 最小K个数(中等)
和上一题“数组中的第K个最大元素”类似。
class Solution {
public:
vector smallestK(vector& arr, int k) {
srand((unsigned int)time(nullptr)); // 设置随机数种子
quickSelect(arr, 0, arr.size() - 1, k);
return { arr.begin(),arr.begin() + k };
}
private:
void quickSelect(vector& nums, int begin, int end, int k)
{
// 递归出口
if (begin >= end)
return;
// 划分左中右三个子区间
vector ret = partition(nums, begin, end);
int left = ret[0];
int right = ret[1];
// 分类讨论
int a = left - begin + 1;
int b = right - left - 1;
if (a > k)
quickSelect(nums, begin, left, k);
else if (a + b >= k)
return;
else
quickSelect(nums, right, end, k - a - b);
}
vector partition(vector& nums, int begin, int end)
{
// 随机取key
int key = nums[rand() % (end - begin + 1) + begin];
// 数组分三块
int left = begin - 1;
int right = end + 1;
int i = begin;
while (i < right)
{
if (nums[i] < key)
{
swap(nums[++left], nums[i++]);
}
else if (nums[i] == key)
{
i++;
}
else
{
swap(nums[--right], nums[i]);
}
}
return { left,right };
}
}; 归并排序:
1. 排序数组(中等)
归并排序的基本思想是基于分治法的:将两个有序表合并成一个新的有序表,这种两两归并的排序方法称为2路归并排序。
class Solution {
public:
vector sortArray(vector& nums) {
mergeSort(nums, 0, nums.size() - 1);
return nums;
}
private:
void mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return;
// 划分左右两个子区间
int mid = (begin + end) / 2;
// 递归排序两个子区间
mergeSort(nums, begin, mid);
mergeSort(nums, mid + 1, end);
// 合并两个有序子区间
merge(nums, begin, mid, end);
}
void merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmp(n);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
// 升序排序
while (begin1 <= end1 && begin2 <= end2)
{
if (nums[begin1] < nums[begin2])
{
tmp[i++] = nums[begin1++];
}
else
{
tmp[i++] = nums[begin2++];
}
}
while (begin1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[begin1++];
}
while (begin2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[begin2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
}
}; 2. 交易逆序对的总数(困难)
如果我们将数组划分为左右两个区间,那么逆序对的选择有3种情况,3种情况下逆序对的总和就是整个数组逆序对的总数。
逆序对中两个元素:
- 全部从左区间中选择
- 全部从右区间中选择
- 一个从左区间中选择,一个从右区间中选择
思路恰好对应了归并排序:递归排序两个子区间,合并两个有序子区间。
我们可以结合归并排序,求出逆序对的数量:
- 求出左区间中逆序对的数量,并对区间排序
- 求出右区间中逆序对的数量,并对区间排序
- 求出“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,并合并两个有序子区间
那么,“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,如何求?
方法一:针对右区间的某数,统计左区间中有多少数比它大。
升序排序的情况:
处理剩余元素:
- 如果左区间有剩余,剩余元素都> 右区间的所有元素,但是它们都已经被统计过了,不会再产生逆序对,直接把剩余元素接到tmp数组后面即可。
- 如果右区间有剩余,剩余元素都>= 左区间的所有元素,不会产生逆序对,直接把剩余元素接到tmp数组后面即可。
降序排序的情况:
处理剩余元素:
- 如果左区间有剩余,剩余元素都<= 右区间的所有元素,不会产生逆序对,直接把剩余元素接到tmp数组后面即可。
- 如果右区间有剩余,剩余元素都< 左区间的所有元素,但是它们都没有被统计过,循环把end1 - begin1 + 1添加到答案并把剩余元素逐个接到tmp数组后面。
显然,方法一用升序排序比降序排序简单,因为不用特殊处理剩余元素。
升序排序版:
class Solution {
public:
int reversePairs(vector& record) {
return mergeSort(record, 0, record.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的逆序对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的逆序对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmp(n);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
int ans = 0;
// 升序排序
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j1] <= nums[j2])
{
tmp[i++] = nums[j1++];
}
else
{
ans += end1 - j1 + 1;
tmp[i++] = nums[j2++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
}; 降序排序版:
class Solution {
public:
int reversePairs(vector& record) {
return mergeSort(record, 0, record.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的逆序对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的逆序对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmp(n);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
int ans = 0;
// 降序排序
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j1] > nums[j2])
{
tmp[i++] = nums[j1++];
}
else
{
ans += j1 - begin1;
tmp[i++] = nums[j2++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
ans += end1 - begin1 + 1;
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
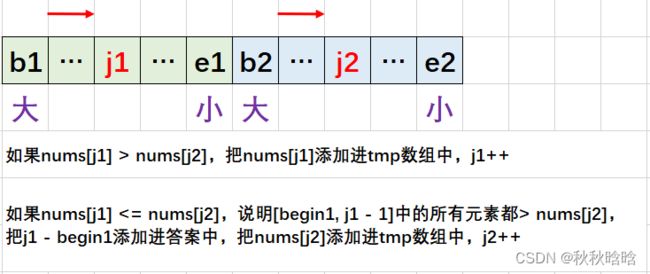
}; 方法二:针对左区间的某数,统计右区间中有多少数比它小。
升序排序的情况:
处理剩余元素:
- 如果左区间有剩余,剩余元素都> 右区间的所有元素,但是它们都没有被统计过,循环把end2 - begin2 + 1添加到答案并把剩余元素逐个接到tmp数组后面。
- 如果右区间有剩余,剩余元素都>= 左区间的所有元素,不会产生逆序对,直接把剩余元素接到tmp数组后面即可。
降序排序的情况:
处理剩余元素:
- 如果左区间有剩余,剩余元素都<= 右区间的所有元素,不会产生逆序对,直接把剩余元素接到tmp数组后面即可。
- 如果右区间有剩余,剩余元素都< 左区间的所有元素,但是它们都已经被统计过了,不会再产生逆序对,直接把剩余元素接到tmp数组后面即可。
显然,方法二用降序排序比升序排序简单,因为不用特殊处理剩余元素。
升序排序版:
class Solution {
public:
int reversePairs(vector& record) {
return mergeSort(record, 0, record.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的逆序对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的逆序对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmp(n);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
int ans = 0;
// 升序排序
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j2] < nums[j1])
{
tmp[i++] = nums[j2++];
}
else
{
ans += j2 - begin2;
tmp[i++] = nums[j1++];
}
}
while (j1 <= end1) // 左区间有剩余
{
ans += end2 - begin2 + 1;
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
}; 降序排序版:
class Solution {
public:
int reversePairs(vector& record) {
return mergeSort(record, 0, record.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的逆序对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的逆序对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的逆序对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmp(n);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
int ans = 0;
// 降序排序
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j2] >= nums[j1])
{
tmp[i++] = nums[j2++];
}
else
{
ans += end2 - j2 + 1;
tmp[i++] = nums[j1++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
}; 3. 计算右侧小于当前元素的个数(困难)
本题是上一题“逆序对”方法二——“针对左区间的某数,统计右区间中有多少数比它小”的拓展。
根据逆序对的经验,方法二用降序排序比升序排序简单,因为不用特殊处理剩余元素。
需要一个索引数组将数组元素和对应的下标绑定在一起。
class Solution {
public:
vector countSmaller(vector& nums) {
int n = nums.size();
ans.resize(n);
index.resize(n);
// 初始化索引数组
for (int i = 0; i < n; i++)
{
index[i] = i;
}
mergeSort(nums, 0, n - 1);
return ans;
}
private:
void mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return;
// 划分左右两个子区间
int mid = (begin + end) / 2;
// 递归处理左右两个区间
mergeSort(nums, begin, mid);
mergeSort(nums, mid + 1, end);
// 处理“针对左区间的某数,统计右区间中有多少数比它小”
merge(nums, begin, mid, end);
return;
}
// 针对左区间的某数,统计右区间中有多少数比它小,并合并两个有序子区间
void merge(vector& nums, int begin, int mid, int end)
{
int n = end - begin + 1;
vector tmpNums(n); // 排序用的辅助数组
vector tmpIndex(n); // 处理下标用的辅助数组
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
// 降序排序
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j2] >= nums[j1])
{
tmpNums[i] = nums[j2];
tmpIndex[i++] = index[j2++];
}
else
{
ans[index[j1]] += end2 - j2 + 1;
tmpNums[i] = nums[j1];
tmpIndex[i++] = index[j1++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmpNums[i] = nums[j1];
tmpIndex[i++] = index[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmpNums[i] = nums[j2];
tmpIndex[i++] = index[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmpNums[i];
index[i + begin] = tmpIndex[i];
}
}
vector ans;
vector index; // 索引数组,index[j]保存当前nums[j]的原始下标
}; 4. 翻转对(困难)
和逆序对类似,所以也可以用归并排序的思想解决问题。
如果我们将数组划分为左右两个区间,那么翻转对的选择有3种情况,3种情况下翻转对的总和就是整个数组翻转对的总数。
翻转对中两个元素:
- 全部从左区间中选择
- 全部从右区间中选择
- 一个从左区间中选择,一个从右区间中选择
和逆序对不同的是,逆序对是在合并有序区间过程中,计算出翻转对的数量,对于翻转对,我们要先计算出翻转对的数量,再合并。
“一个从左区间中选择,一个从右区间中选择”的翻转对的数量,如何求?
方法一:针对右区间的某数,统计左区间中有多少数比它的2倍大。
根据逆序对的经验,方法一用升序排序比降序排序简单,因为不用特殊处理剩余元素。
class Solution {
public:
int reversePairs(vector& nums) {
return mergeSort(nums, 0, nums.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的翻转对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的翻转对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的翻转对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int ans = 0;
// 升序排序的情况下翻转对的数量
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
while (j1 <= end1 && nums[j1] / 2.0 <= nums[j2]) // 防止2 * nums[j2]溢出
{
j1++;
}
if (j1 > end1)
break;
ans += end1 - j1 + 1;
j2++;
}
// 合并升序排序的两个区间
int n = end - begin + 1;
vector tmp(n);
int i = 0;
j1 = begin1;
j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j1] < nums[j2])
{
tmp[i++] = nums[j1++];
}
else
{
tmp[i++] = nums[j2++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
}; 方法二:针对左区间的某数,统计右区间中有多少数的2倍比它小。
根据逆序对的经验,方法二用降序排序比升序排序简单,因为不用特殊处理剩余元素。
class Solution {
public:
int reversePairs(vector& nums) {
return mergeSort(nums, 0, nums.size() - 1);
}
private:
int mergeSort(vector& nums, int begin, int end)
{
// 递归出口
if (begin >= end)
return 0;
// 划分左右两个子区间
int mid = (begin + end) / 2;
int ans = 0;
// 分别将左右两个区间的翻转对的数量添加进答案中
ans += mergeSort(nums, begin, mid);
ans += mergeSort(nums, mid + 1, end);
// 将“一个从左区间中选择,一个从右区间中选择”的翻转对的数量添加进答案中
ans += merge(nums, begin, mid, end);
return ans;
}
// 求出“一个从左区间中选择,一个从右区间中选择”的翻转对的数量,并合并两个有序子区间
int merge(vector& nums, int begin, int mid, int end)
{
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int ans = 0;
// 降序排序的情况下翻转对的数量
int j1 = begin1, j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
while (j2 <= end2 && nums[j2] >= nums[j1] / 2.0) // 防止2 * nums[j2]溢出
{
j2++;
}
if (j2 > end2)
break;
ans += end2 - j2 + 1;
j1++;
}
// 合并降序排序的两个区间
int n = end - begin + 1;
vector tmp(n);
int i = 0;
j1 = begin1;
j2 = begin2;
while (j1 <= end1 && j2 <= end2)
{
if (nums[j1] > nums[j2])
{
tmp[i++] = nums[j1++];
}
else
{
tmp[i++] = nums[j2++];
}
}
while (j1 <= end1) // 左区间有剩余
{
tmp[i++] = nums[j1++];
}
while (j2 <= end2) // 右区间有剩余
{
tmp[i++] = nums[j2++];
}
// 拷贝
for (int i = 0; i < n; i++)
{
nums[i + begin] = tmp[i];
}
return ans;
}
}; 5. 排序链表(中等)
分治的思想,类似归并排序:
-
划分两个子链表
-
分别对两个子链表进行排序,形成两个有序链表
-
合并两个有序链表
重复的子问题——函数头设计
ListNode* sortList(ListNode* head)
子问题在做什么——函数体设计
- 划分两个子链表,找中间节点:ListNode* mid = midNode(head);
- 递归排序右子链表:ListNode* l1 = sortList(mid->next);
- 断开两个子链表:mid->next = nullptr;
- 递归排序左子链表:ListNode* l2 = sortList(head);
- 合并两个有序链表:return mergeTowList(l1, l2);
递归出口
当链表只有一个节点时,不合并。另外,当题目给出空链表时,不合并。
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr)
return head;
ListNode* mid = midNode(head); // 中间节点
ListNode* l1 = sortList(mid->next); // 排序右子链表
mid->next = nullptr; // 断开两个子链表
ListNode* l2 = sortList(head); // 排序左子链表
return mergeTwoLists(l1, l2); // 合并两个有序链表
}
private:
// 快慢指针找链表的中间节点,如果节点个数为偶数,取靠左的
ListNode* midNode(ListNode* head)
{
ListNode* fast = head;
ListNode* slow = head;
// 慢指针每次走1步,快指针每次走2步
// 如果节点个数为奇数,当快指针指向最后一个节点时,慢指针指向中间节点
// 如果节点个数为奇数,当快指针指向倒数第二个节点时,慢指针指向靠左的中间节点
while (fast->next && fast->next->next)
{
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
// 合并两个有序链表
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
ListNode* preHead = new ListNode; // 哨兵节点
ListNode* tail = preHead;
// 取小的尾插
while (list1 && list2)
{
if (list1->val < list2->val)
{
tail->next = list1;
tail = tail->next;
list1 = list1->next;
}
else
{
tail->next = list2;
tail = tail->next;
list2 = list2->next;
}
}
if (list1)
{
tail->next = list1;
}
if (list2)
{
tail->next = list2;
}
return preHead->next;
}
};6. 合并 K 个升序链表(困难)
6.1 递归解法(归并)
分治的思想,类似归并排序:
-
划分两个子区间
-
分别对两个子区间的链表进行合并,形成两个有序链表
-
合并两个有序链表
重复的子问题——函数头设计
ListNode* merge(vector
子问题在做什么——函数体设计
- 划分两个子区间:int mid = (begin + end) / 2;
- 递归合并两个子区间:
ListNode* l1 = merge(lists, begin, mid);
ListNode* l2 = merge(lists, mid + 1, end); - 合并两个有序链表:return mergeTowList(l1, l2);
递归出口
当区间只有一个链表时,不合并。另外,当题目给出空链表时,不合并。
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
return merge(lists, 0, lists.size() - 1);
}
private:
ListNode* merge(vector& lists, int begin, int end)
{
if (begin > end)
return nullptr;
if (begin == end)
return lists[begin];
int mid = (begin + end) / 2;
ListNode* l1 = merge(lists, begin, mid);
ListNode* l2 = merge(lists, mid + 1, end);
return mergeTwoLists(l1, l2);
}
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
ListNode* preHead = new ListNode; // 哨兵节点
ListNode* tail = preHead;
// 取小的尾插
while (list1 && list2)
{
if (list1->val < list2->val)
{
tail->next = list1;
tail = tail->next;
list1 = list1->next;
}
else
{
tail->next = list2;
tail = tail->next;
list2 = list2->next;
}
}
if (list1)
{
tail->next = list1;
}
if (list2)
{
tail->next = list2;
}
return preHead->next;
}
}; 6.2 迭代解法(堆)
和“合并两个有序链表”类似,就是取小的尾插。怎么判断K个链表未合并的头节点中最小的那个?利用堆这个数据结构即可。把K个链表未合并的头节点放进一个小根堆,堆顶就是最小的那个。
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
// 创建小根堆
priority_queue, cmp> heap;
// 将所有头节点放进小根堆
for (auto& l : lists)
{
if (l)
{
heap.push(l);
}
}
// 合并链表
ListNode* preHead = new ListNode; // 哨兵节点
ListNode* tail = preHead;
while (!heap.empty())
{
// 取堆顶节点尾插
tail->next = heap.top();
heap.pop();
tail = tail->next;
// 将刚才合并的节点的下一个节点补充进堆
if (tail->next)
{
heap.push(tail->next);
}
}
return preHead->next;
}
private:
struct cmp
{
bool operator()(ListNode* n1, ListNode* n2)
{
return n1->val > n2->val;
}
};
};