Numpy的基础知识
文章目录
- Numerical Python介绍
- 基础数据结构ndarray数组
-
- 为什么引入ndarray数组
-
- ndarray数组和list列表分别完成对每个元素增加1的计算
- ndarray数组和list列表分别完成相加计算
- 如何创建ndarray数组
-
- 查看ndarray数组的属性
- 改变ndarray数组的数据类型和形状
- ndarray数组的基本运算
-
- 标量和ndarray数组之间的运算
- 两个ndarray数组之间的运算
- ndarray数组的索引和切片
- ndarray数组的统计运算
- 随机数np.random
-
-
- 创建随机ndarray数组
- 设置随机数种子
- 随机打乱ndarray数组顺序
- 随机选取元素
-
- 线性代数
- Numpy保存和导入文件
- Numpy应用举例
-
- Numpy应用举例——计算激活函数
- Numpy应用举例——图像翻转和裁剪
- 课程作业
-
- 1 使用numpy计算tanh激活函数
- 2 统计随机生成矩阵中有多少个元素大于0
Numerical Python介绍
Numpy是Numerical Python的简称,是Python中高性能科学计算和数据分析的基础包。Numpy提供了一个多维数组类型ndarray,它具有矢量算术运算和复杂广播的能力,可以实现快速的计算并且能节省存储空间。在使用Python调用飞桨API完成深度学习任务的过程中,通常会使用Numpy实现数据预处理和一些模型指标的计算,飞桨中的Tensor数据可以很方便的和ndarray数组进行相互转换。
参考资料
在这一节将介绍以下内容:
-
基础数据结构ndarray数组
-
随机数numpy.random
-
线性代数numpy.linalg
-
Numpy保存和导入文件
-
应用举例
-
课后作业
基础数据结构ndarray数组
ndarray数组是Numpy中的基础数据结构式,这一小节将从以下几个方面展开进行介绍:
-
为什么引入ndarray数组
-
如何创建ndarray数组
-
ndarray数组的基本运算
-
ndarray数组的切片和索引
-
ndarray数组的统计运算
为什么引入ndarray数组
在Python中使用list列表可以非常灵活的处理多个元素的操作,但是其效率却比较低。ndarray数组相比于Python中的list列表具有以下特点:
-
ndarray数组中所有元素的数据类型是相同的,数据地址是连续的,批量操作数组元素时速度更快;list列表中元素的数据类型可以不同,需要通过寻址方式找到下一个元素
-
ndarray数组中实现了比较成熟的广播机制,矩阵运算时不需要写for循环
-
Numpy底层是用c语言编写的,内置了并行计算功能,运行速度高于纯Python代码
下面的代码展示了使用ndarray数组和list列表完成相同的任务,ndarray数组的代码看上去要更加简洁而且易于理解。
ndarray数组和list列表分别完成对每个元素增加1的计算
# Python原生的list
# 假设有两个list
a = [1, 2, 3, 4, 5]
b = [2, 3, 4, 5, 6]
# 完成如下计算
# 1 对a的每个元素 + 1
# a = a + 1 不能这么写,会报错
# a[:] = a[:] + 1 也不能这么写,也会报错
for i in range(5):
a[i] = a[i] + 1
a
[2, 3, 4, 5, 6]
# 使用ndarray
import numpy as np
a = np.array([1, 2, 3, 4, 5])
a = a + 1
a
array([2, 3, 4, 5, 6])
ndarray数组和list列表分别完成相加计算
# 2 计算 a和b中对应位置元素的和,是否可以这么写?
a = [1, 2, 3, 4, 5]
b = [2, 3, 4, 5, 6]
c = a + b
# 检查输出发现,不是想要的结果
c
[1, 2, 3, 4, 5, 2, 3, 4, 5, 6]
# 使用for循环,完成两个list对应位置元素相加
c = []
for i in range(5):
c.append(a[i] + b[i])
c
[3, 5, 7, 9, 11]
# 使用numpy中的ndarray完成两个ndarray相加
import numpy as np
a = np.array([1, 2, 3, 4, 5])
b = np.array([2, 3, 4, 5, 6])
c = a + b
c
array([ 3, 5, 7, 9, 11])
从上面的示例中可以看出,ndarray数组的矢量计算能力使得不需要写for循环,就可以非常方便的完成数学计算,在操作矢量或者矩阵时,可以像操作普通的数值变量一样编写程序,使得代码极其简洁。另外,ndarray数组还提供了广播机制,它会按一定规则自动对数组的维度进行扩展以完成计算,如下面例子所示,1维数组和2维数组进行相加操作,ndarray数组会自动扩展1维数组的维度,然后再对每个位置的元素分别相加。
# 自动广播机制,1维数组和2维数组相加
# 二维数组维度 2x5
# array([[ 1, 2, 3, 4, 5],
# [ 6, 7, 8, 9, 10]])
d = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
# c是一维数组,维度5
# array([ 4, 6, 8, 10, 12])
c = np.array([ 4, 6, 8, 10, 12])
e = d + c
e
array([[ 5, 8, 11, 14, 17],
[10, 13, 16, 19, 22]])
如何创建ndarray数组
这一小节将介绍如何创建ndarray数组,以及如何查看并修改它的属性
有如下几种方式创建ndarray数组
-
从list列表创建
-
指定起止范围及间隔创建
-
创建值全为0的ndarray数组
-
创建值全为1的ndarray数组
# 导入numpy
import numpy as np
# 从list创建array
a = [1,2,3,4,5,6]
b = np.array(a)
b
array([1, 2, 3, 4, 5, 6])
# 通过np.arange创建
# 通过指定start, stop (不包括stop),interval来产生一个1为的ndarray
a = np.arange(0, 20, 2)
a
array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
# 创建全0的ndarray
a = np.zeros([3,3])
a
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
# 创建全1的ndarray
a = np.ones([3,3])
a
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
查看ndarray数组的属性
ndarray的属性包括形状shape、数据类型dtype、元素个数size和维度ndim等,下面的程序展示如何查看这些属性
# 数组的数据类型 ndarray.dtype
# 数组的形状 ndarray.shape,1维数组(N, ),二维数组(M, N),三维数组(M, N, K)
# 数组的维度大小,ndarray.ndim, 其大小等于ndarray.shape所包含元素的个数
# 数组中包含的元素个数 ndarray.size,其大小等于各个维度的长度的乘积
a = np.ones([3, 3])
print('a, dtype: {}, shape: {}, size: {}, ndim: {}'.format(a.dtype, a.shape, a.size, a.ndim))
a, dtype: float64, shape: (3, 3), size: 9, ndim: 2
改变ndarray数组的数据类型和形状
创建ndarray之后,可以对其数据类型进行更改,或者对形状进行调整,如下面的代码所示
# 转化数据类型
b = a.astype(np.int64)
print('b, dtype: {}, shape: {}'.format(b.dtype, b.shape))
# 改变形状
c = a.reshape([1, 9])
print('c, dtype: {}, shape: {}'.format(c.dtype, c.shape))
b, dtype: int64, shape: (3, 3)
c, dtype: float64, shape: (1, 9)
ndarray数组的基本运算
ndarray数组可以像普通的数值型变量一样进行加减乘除操作,这一小节将介绍两种形式的基本运算:
-
标量和ndarray数组之间的运算
-
两个ndarray数组之间的运算
标量和ndarray数组之间的运算
# 标量除以数组,用标量除以数组的每一个元素
arr = np.array([[1., 2., 3.], [4., 5., 6.]])
1. / arr
array([[1. , 0.5 , 0.33333333],
[0.25 , 0.2 , 0.16666667]])
# 标量乘以数组,用标量乘以数组的每一个元素
arr = np.array([[1., 2., 3.], [4., 5., 6.]])
2.0 * arr
array([[ 2., 4., 6.],
[ 8., 10., 12.]])
# 标量加上数组,用标量加上数组的每一个元素
arr = np.array([[1., 2., 3.], [4., 5., 6.]])
2.0 + arr
array([[3., 4., 5.],
[6., 7., 8.]])
# 标量减去数组,用标量减去数组的每一个元素
arr = np.array([[1., 2., 3.], [4., 5., 6.]])
2.0 - arr
array([[ 1., 0., -1.],
[-2., -3., -4.]])
两个ndarray数组之间的运算
# 数组 减去 数组, 用对应位置的元素相减
arr1 = np.array([[1., 2., 3.], [4., 5., 6.]])
arr2 = np.array([[11., 12., 13.], [21., 22., 23.]])
arr1 - arr2
array([[-10., -10., -10.],
[-17., -17., -17.]])
# 数组 加上 数组, 用对应位置的元素相加
arr1 = np.array([[1., 2., 3.], [4., 5., 6.]])
arr2 = np.array([[11., 12., 13.], [21., 22., 23.]])
arr1 + arr2
array([[12., 14., 16.],
[25., 27., 29.]])
# 数组 乘以 数组,用对应位置的元素相乘
arr1 * arr2
array([[ 11., 24., 39.],
[ 84., 110., 138.]])
# 数组 除以 数组,用对应位置的元素相除
arr1 / arr2
array([[0.09090909, 0.16666667, 0.23076923],
[0.19047619, 0.22727273, 0.26086957]])
# 数组开根号,将每个位置的元素都开根号
arr ** 0.5
array([[1. , 1.41421356, 1.73205081],
[2. , 2.23606798, 2.44948974]])
ndarray数组的索引和切片
在程序中,通常需要访问或者修改ndarray数组某个位置的元素,也就是要用到ndarray数组的索引;有些情况下可能需要访问或者修改一些区域的元素,则需要使用数组的切片。索引和切片的使用方式与Python中的list类似,ndarray数组可以基于 -n ~ n-1 的下标进行索引,切片对象可以通过内置的 slice 函数,并设置 start, stop 及 step 参数进行,从原数组中切割出一个新数组。
# 1维数组索引和切片
a = np.arange(30)
a[10]
10
a = np.arange(30)
b = a[4:7]
b
array([4, 5, 6])
#将一个标量值赋值给一个切片时,该值会自动传播到整个选区(如下图所示)
a = np.arange(30)
a[4:7] = 10
a
array([ 0, 1, 2, 3, 10, 10, 10, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29])
# 数组切片是原始数组的视图。这意味着数据不会被复制,
# 视图上的任何修改都会直接反映到源数组上
a = np.arange(30)
arr_slice = a[4:7]
arr_slice[0] = 100
a, arr_slice
(array([ 0, 1, 2, 3, 100, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
26, 27, 28, 29]), array([100, 5, 6]))
# 通过copy给新数组创建不同的内存空间
a = np.arange(30)
arr_slice = a[4:7]
arr_slice = np.copy(arr_slice)
arr_slice[0] = 100
a, arr_slice
(array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]),
array([100, 5, 6]))
# 多维数组索引和切片
a = np.arange(30)
arr3d = a.reshape(5, 3, 2)
arr3d
array([[[ 0, 1],
[ 2, 3],
[ 4, 5]],
[[ 6, 7],
[ 8, 9],
[10, 11]],
[[12, 13],
[14, 15],
[16, 17]],
[[18, 19],
[20, 21],
[22, 23]],
[[24, 25],
[26, 27],
[28, 29]]])
# 只有一个索引指标时,会在第0维上索引,后面的维度保持不变
arr3d[0]
array([[0, 1],
[2, 3],
[4, 5]])
# 两个索引指标
arr3d[0][1]
array([2, 3])
# 两个索引指标
arr3d[0, 1]
array([2, 3])
# 使用python中的for语法对数组切片
a = np.arange(24)
a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
a = a.reshape([6, 4])
a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
# 使用for语句生成list
[k for k in range(0, 6, 2)]
[0, 2, 4]
# 结合上面列出的for语句的用法
# 使用for语句对数组进行切片
# 下面的代码会生成多个切片构成的list
# k in range(0, 6, 2) 决定了k的取值可以是0, 2, 4
# 产生的list的包含三个切片
# 第一个元素是a[0 : 0+2],
# 第二个元素是a[2 : 2+2],
# 第三个元素是a[4 : 4+2]
slices = [a[k:k+2] for k in range(0, 6, 2)]
slices
[array([[0, 1, 2, 3],
[4, 5, 6, 7]]), array([[ 8, 9, 10, 11],
[12, 13, 14, 15]]), array([[16, 17, 18, 19],
[20, 21, 22, 23]])]
slices[0]
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
ndarray数组的统计运算
这一小节将介绍如何计算ndarray数组的各个统计量,包括以下几项:
- mean 均值
- std 标准差
- var 方差
- sum 求和
- max 最大值
- min 最小值
# 计算均值,使用arr.mean() 或 np.mean(arr),二者是等价的
arr = np.array([[1,2,3], [4,5,6], [7,8,9]])
arr.mean(), np.mean(arr)
(5.0, 5.0)
# 求和
arr.sum(), np.sum(arr)
(45, 45)
# 求最大值
arr.max(), np.max(arr)
(9, 9)
# 求最小值
arr.min(), np.min(arr)
(1, 1)
# 指定计算的维度
# 沿着第1维求平均,也就是将[1, 2, 3]取平均等于2,[4, 5, 6]取平均等于5,[7, 8, 9]取平均等于8
arr.mean(axis = 1)
array([2., 5., 8.])
# 沿着第0维求和,也就是将[1, 4, 7]求和等于12,[2, 5, 8]求和等于15,[3, 6, 9]求和等于18
arr.sum(axis=0)
array([12, 15, 18])
# 沿着第0维求最大值,也就是将[1, 4, 7]求最大值等于7,[2, 5, 8]求最大值等于8,[3, 6, 9]求最大值等于9
arr.max(axis=0)
array([7, 8, 9])
# 沿着第1维求最小值,也就是将[1, 2, 3]求最小值等于1,[4, 5, 6]求最小值等于4,[7, 8, 9]求最小值等于7
arr.min(axis=1)
array([1, 4, 7])
# 计算标准差
arr.std()
2.581988897471611
# 计算方差
arr.var()
6.666666666666667
# 找出最大元素的索引
arr.argmax(), arr.argmax(axis=0), arr.argmax(axis=1)
(8, array([2, 2, 2]), array([2, 2, 2]))
# 找出最小元素的索引
arr.argmin(), arr.argmin(axis=0), arr.argmin(axis=1)
(0, array([0, 0, 0]), array([0, 0, 0]))
随机数np.random
-
创建随机ndarray数组
-
设置随机数种子
-
随机打乱顺序
-
随机选取元素
创建随机ndarray数组
# 生成均匀分布随机数,随机数取值范围在[0, 1)之间
a = np.random.rand(3, 3)
a
array([[0.08833981, 0.68535982, 0.95339335],
[0.00394827, 0.51219226, 0.81262096],
[0.61252607, 0.72175532, 0.29187607]])
# 生成均匀分布随机数,指定随机数取值范围和数组形状
a = np.random.uniform(low = -1.0, high = 1.0, size=(2,2))
a
array([[ 0.83554825, 0.42915157],
[ 0.08508874, -0.7156599 ]])
# 生成标准正态分布随机数
a = np.random.randn(3, 3)
a
array([[ 1.484537 , -1.07980489, -1.97772828],
[-1.7433723 , 0.26607016, 2.38496733],
[ 1.12369125, 1.67262221, 0.09914922]])
# 生成正态分布随机数,指定均值loc和方差scale
a = np.random.normal(loc = 1.0, scale = 1.0, size = (3,3))
a
array([[2.39799638, 0.72875201, 1.61320418],
[0.73268281, 0.45069099, 1.1327083 ],
[0.52385799, 2.30847308, 1.19501328]])
设置随机数种子
# 可以多次运行,观察程序输出结果是否一致
# 如果不设置随机数种子,观察多次运行输出结果是否一致
np.random.seed(10)
a = np.random.rand(3, 3)
a
array([[0.77132064, 0.02075195, 0.63364823],
[0.74880388, 0.49850701, 0.22479665],
[0.19806286, 0.76053071, 0.16911084]])
随机打乱ndarray数组顺序
# 生成一维数组
a = np.arange(0, 30)
# 打乱一维数组顺序
print('before random shuffle: ', a)
np.random.shuffle(a)
print('after random shuffle: ', a)
('before random shuffle: ', array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]))
('after random shuffle: ', array([10, 21, 26, 7, 0, 23, 2, 17, 18, 20, 12, 6, 9, 3, 25, 5, 13,
14, 24, 29, 1, 28, 11, 15, 27, 16, 19, 4, 22, 8]))
# 生成一维数组
a = np.arange(0, 30)
# 将一维数组转化成2维数组
a = a.reshape(10, 3)
# 打乱一维数组顺序
print('before random shuffle: \n{}'.format(a))
np.random.shuffle(a)
print('after random shuffle: \n{}'.format(a))
before random shuffle:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]
[12 13 14]
[15 16 17]
[18 19 20]
[21 22 23]
[24 25 26]
[27 28 29]]
after random shuffle:
[[15 16 17]
[12 13 14]
[27 28 29]
[ 3 4 5]
[ 9 10 11]
[21 22 23]
[18 19 20]
[ 0 1 2]
[ 6 7 8]
[24 25 26]]
随机打乱1维数组顺序时,发现所有元素位置都改变了;随机打乱二维数组顺序时,发现只有第行的顺序被打乱了,列的顺序保持不变。
随机选取元素
# 随机选取一选部分元素
a = np.arange(30)
b = np.random.choice(a, size=5)
b
array([ 0, 24, 12, 5, 4])
线性代数
Numpy中实现了线性代数中常用的各种操作,并形成了numpy.linalg线性代数相关的模块。其中包括:
- diag 以一维数组的形式返回方阵的对角线(或非对角线)元素,或将一维数组转换为方阵(非对角线元素为0)
- dot 矩阵乘法
- trace 计算对角线元素的和
- det 计算矩阵行列式
- eig 计算方阵的特征值和特征向量
- inv 计算方阵的逆
感兴趣的读者可以查看各个操作相关的文档,或者np.linalg的文档以了解更多操作。
# 矩阵相乘
a = np.arange(12)
b = a.reshape([3, 4])
c = a.reshape([4, 3])
# 矩阵b的第二维大小,必须等于矩阵c的第一维大小
d = b.dot(c) # 等价于 np.dot(b, c)
print('a: \n{}'.format(a))
print('b: \n{}'.format(b))
print('c: \n{}'.format(c))
print('d: \n{}'.format(d))
a:
[ 0 1 2 3 4 5 6 7 8 9 10 11]
b:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
c:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
d:
[[ 42 48 54]
[114 136 158]
[186 224 262]]
# numpy.linalg 中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西
# np.linalg.diag 以一维数组的形式返回方阵的对角线(或非对角线)元素,
# 或将一维数组转换为方阵(非对角线元素为0)
e = np.diag(d)
f = np.diag(e)
print('d: \n{}'.format(d))
print('e: \n{}'.format(e))
print('f: \n{}'.format(f))
d:
[[ 42 48 54]
[114 136 158]
[186 224 262]]
e:
[ 42 136 262]
f:
[[ 42 0 0]
[ 0 136 0]
[ 0 0 262]]
# trace, 计算对角线元素的和
g = np.trace(d)
g
440
# det,计算行列式
h = np.linalg.det(d)
h
1.3642420526593978e-11
# eig,计算特征值和特征向量
i = np.linalg.eig(d)
i
(array([4.36702561e+02, 3.29743887e+00, 3.13152204e-14]),
array([[ 0.17716392, 0.77712552, 0.40824829],
[ 0.5095763 , 0.07620532, -0.81649658],
[ 0.84198868, -0.62471488, 0.40824829]]))
# inv,计算方阵的逆
tmp = np.random.rand(3, 3)
j = np.linalg.inv(tmp)
j
array([[-0.59449952, 1.39735912, -0.06654123],
[ 1.56034184, -0.40734618, -0.48055062],
[ 0.10659811, -0.62164179, 1.30437759]])
Numpy保存和导入文件
Numpy还可以方便的进行文件读写,比如对于下面这种格式的文本文件:
![]()
# 使用np.fromfile从文本文件'housing.data'读入数据
# 这里要设置参数sep = ' ',表示使用空白字符来分隔数据
# 空格或者回车都属于空白字符,读入的数据被转化成1维数组
d = np.fromfile('./work/housing.data', sep = ' ')
d
array([6.320e-03, 1.800e+01, 2.310e+00, ..., 3.969e+02, 7.880e+00,
1.190e+01])
Numpy还提供了save和load接口,直接将数组保存成文件(保存为.npy格式),或者从.npy文件中读取数组
# 产生随机数组a
a = np.random.rand(3,3)
np.save('a.npy', a)
# 从磁盘文件'a.npy'读入数组
b = np.load('a.npy')
# 检查a和b的数值是否一样
check = (a == b).all()
check
True
Numpy应用举例
上面的章节中介绍了Numpy中的基础数据结构ndarray数组和一些基本操作,这一小节将使用这些操作来实现两个简单的例子。
-
应用Numpy计算激活函数
-
应用Numpy处理图像
Numpy应用举例——计算激活函数
使用ndarray数组可以很方便的构建数学函数,而且能利用其底层的矢量计算能力快速实现计算。神经网络中比较常用激活函数是Sigmoid和ReLU,其定义如下。
- Sigmoid激活函数
y = 1 1 + e − x y = \frac{1}{1 + e^{-x}} y=1+e−x1
- ReLU激活函数
y = { 0 , ( x < 0 ) x , ( x ≥ 0 ) y=\left\{ \begin{aligned} 0 & , & (x<0) \\ x & , & (x\ge 0) \end{aligned} \right. y={0x,,(x<0)(x≥0)
下面使用numpy和matplotlib计算函数值并画出图形
# ReLU和Sigmoid激活函数示意图
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.patches as patches
#设置图片大小
plt.figure(figsize=(8, 3))
# x是1维数组,数组大小是从-10. 到10.的实数,每隔0.1取一个点
x = np.arange(-10, 10, 0.1)
# 计算 Sigmoid函数
s = 1.0 / (1 + np.exp(- x))
# 计算ReLU函数
y = np.clip(x, a_min = 0., a_max = None)
#########################################################
# 以下部分为画图程序
# 设置两个子图窗口,将Sigmoid的函数图像画在左边
f = plt.subplot(121)
# 画出函数曲线
plt.plot(x, s, color='r')
# 添加文字说明
plt.text(-5., 0.9, r'$y=\sigma(x)$', fontsize=13)
# 设置坐标轴格式
currentAxis=plt.gca()
currentAxis.xaxis.set_label_text('x', fontsize=15)
currentAxis.yaxis.set_label_text('y', fontsize=15)
# 将ReLU的函数图像画在左边
f = plt.subplot(122)
# 画出函数曲线
plt.plot(x, y, color='g')
# 添加文字说明
plt.text(-3.0, 9, r'$y=ReLU(x)$', fontsize=13)
# 设置坐标轴格式
currentAxis=plt.gca()
currentAxis.xaxis.set_label_text('x', fontsize=15)
currentAxis.yaxis.set_label_text('y', fontsize=15)
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-11LzvNa1-1577262178618)(output_89_0.png)]
Numpy应用举例——图像翻转和裁剪
图像是由像素点构成的矩阵,其数值可以用ndarray来表示。可以将上面章节中介绍的操作用在图像数据对应的ndarray上,并且通过图像直观的展示出它的效果来。
# 导入需要的包
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# 读入图片
image = Image.open('./work/images/000000001584.jpg')
image = np.array(image)
# 查看数据形状,其形状是[H, W, 3],
# 其中H代表高度, W是宽度,3代表RGB三个通道
image.shape
(612, 612, 3)
# 原始图片
plt.imshow(image)
# 垂直方向翻转
# 这里使用数组切片的方式来完成,
# 相当于将图片最后一行挪到第一行,
# 倒数第二行挪到第二行,...,
# 第一行挪到倒数第一行
# 对于行指标,使用::-1来表示切片,
# 负数步长表示以最后一个元素为起点,向左走寻找下一个点
# 对于列指标和RGB通道,仅使用:表示该维度不改变
image2 = image[::-1, :, :]
plt.imshow(image2)
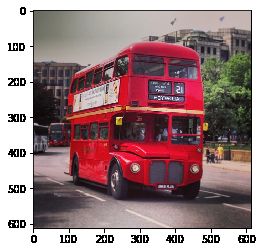
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tCrm8yqy-1577262178618)(output_93_1.png)]
# 水平方向翻转
image3 = image[:, ::-1, :]
plt.imshow(image3)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WOWaRnI2-1577262178618)(output_94_1.png)]
# 保存图片
im3 = Image.fromarray(image3)
im3.save('im3.jpg')
# 高度方向裁剪
H, W = image.shape[0], image.shape[1]
# 注意此处用整除,H_start必须为整数
H1 = H // 2
H2 = H
image4 = image[H1:H2, :, :]
plt.imshow(image4)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ljcZGuYq-1577262178618)(output_96_1.png)]
# 宽度方向裁剪
W1 = W//6
W2 = W//3 * 2
image5 = image[:, W1:W2, :]
plt.imshow(image5)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E6kvHVg7-1577262178619)(output_97_1.png)]
# 两个方向同时裁剪
image5 = image[H1:H2, \
W1:W2, :]
plt.imshow(image5)
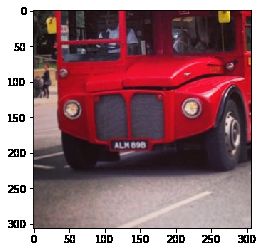
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Jjv8D0HL-1577262178619)(output_98_1.png)]
# 调整亮度
image6 = image * 0.5
plt.imshow(image6.astype('uint8'))
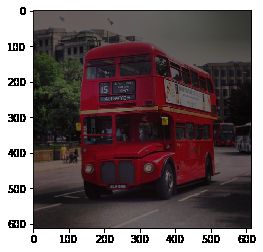
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MtFwM8Ty-1577262178619)(output_99_1.png)]
# 调整亮度
image7 = image * 2.0
# 由于图片的RGB像素值必须在0-255之间,
# 此处使用np.clip进行数值裁剪
image7 = np.clip(image7, \
a_min=None, a_max=255.)
plt.imshow(image7.astype('uint8'))

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CMQqI06s-1577262178619)(output_100_1.png)]
#高度方向每隔一行取像素点
image8 = image[::2, :, :]
plt.imshow(image8)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lYSGtmFj-1577262178619)(output_101_1.png)]
#宽度方向每隔一列取像素点
image9 = image[:, ::2, :]
plt.imshow(image9)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ziPQyR1Z-1577262178620)(output_102_1.png)]
#间隔行列采样,图像尺寸会减半,清晰度变差
image10 = image[::2, ::2, :]
plt.imshow(image10)
image10.shape
(306, 306, 3)
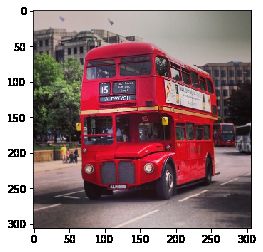
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZS97gIWI-1577262178620)(output_103_1.png)]
课程作业
1 使用numpy计算tanh激活函数
tanh也是神经网络中常用的一种激活函数,其定义如下:
y = e x − e − x e x + e − x y = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} y=ex+e−xex−e−x
请参照讲义中Sigmoid激活函数的计算程序,用numpy实现tanh函数的计算,并画出其函数曲线
提交方式:请用numpy写出计算程序,并画出tanh函数曲线图,x的取值范围设置为[-10., 10.]
2 统计随机生成矩阵中有多少个元素大于0
假设使用np.random.randn生成了随机数构成的矩阵:
p = np.random.randn(10, 10)
请写一段程序统计其中有多少个元素大于0?
提示:可以试下使用 q = (p > 0),观察q是什么的数据类型和元素的取值
提交方式:提交计算的代码,能够直接运行输出统计出来的结果
