2023年 MCM美赛 C题 Wordle预测问题 求解！

---

2023年 MCM美赛 C题 Wordle预测问题 求解！

问题一

• 报告结果的数量( Number of reported results)每天都在变化。
  • 开发一个模型来解释这种变化，
  • 并使用您的模型为 2023 年 3 月 1 日报告的结果数量创建一个预测区间。
  • 这个词的任何属性是否会影响报告的在困难模式下播放的分数的百分比？如果是这样，如何？如果不是，为什么不呢？

读取数据

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import LabelEncoder
import lightgbm as lgb
from datetime import date, timedelta

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
import seaborn as sns
%matplotlib inline

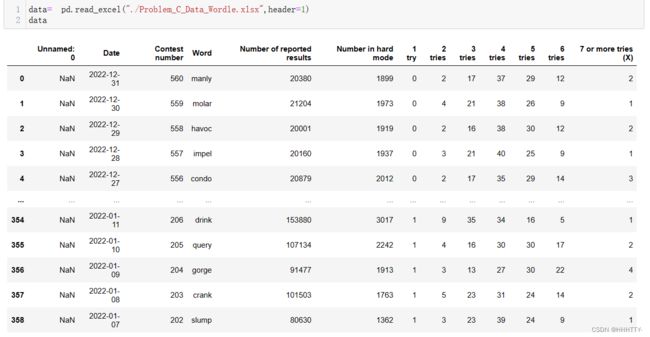
data=  pd.read_excel("./Problem_C_Data_Wordle.xlsx",header=1)
data

---

数据预处理

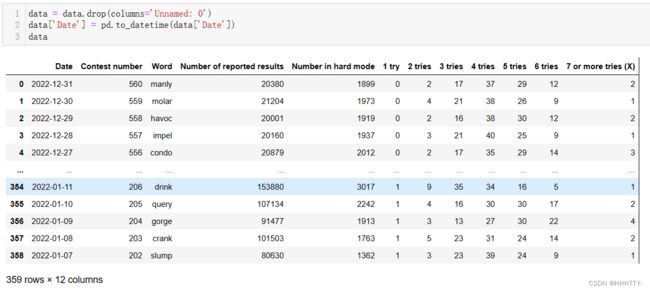
data = data.drop(columns='Unnamed: 0')
data['Date'] = pd.to_datetime(data['Date'])
data

data.set_index("Date", inplace=True)
data.sort_index(ascending=True,inplace=True)

data=data.reset_index()
data

---

数据分析

数据变化趋势

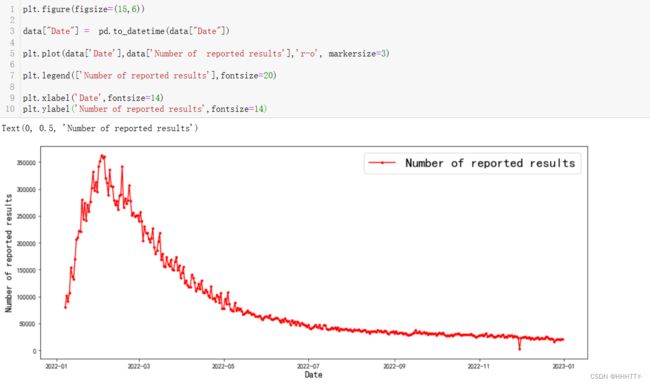
plt.figure(figsize=(15,6))

data["Date"] =  pd.to_datetime(data["Date"])

plt.plot(data['Date'],data['Number of  reported results'],'r-o', markersize=3)

plt.legend(['Number of reported results'],fontsize=20)

plt.xlabel('Date',fontsize=14)
plt.ylabel('Number of reported results',fontsize=14)

---

数据分布

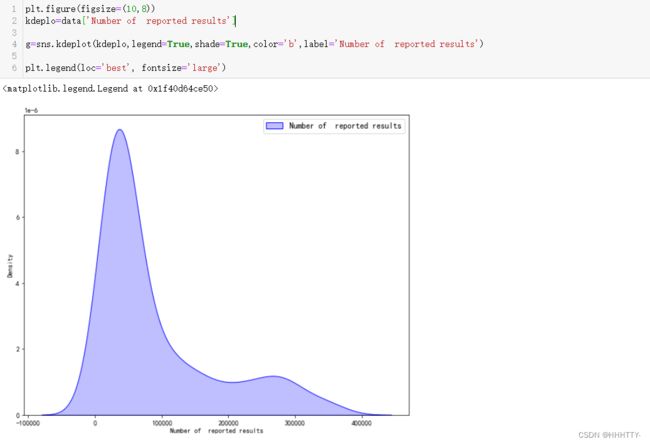
plt.figure(figsize=(10,8))
kdeplo=data['Number of  reported results']

g=sns.kdeplot(kdeplo,legend=True,shade=True,color='b',label='Number of  reported results') 

plt.legend(loc='best', fontsize='large')  

from scipy.stats import norm, skew
plt.figure(figsize=(10,8))
(mu, sigma) = norm.fit(data['Number of  reported results'])
print('\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
g = sns.distplot(data['Number of  reported results'], fit=norm)
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
           loc='best')

g.set(ylabel='Frequency') 
g.set(title=' distribution')
plt.show()

---

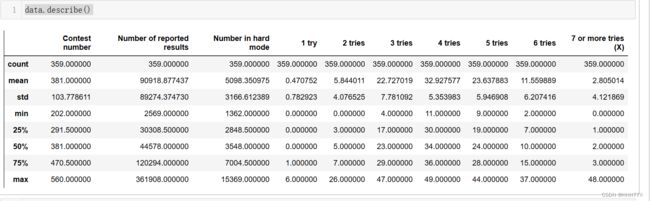
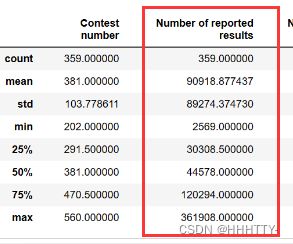
数据统计—— 均值、方差、极大极小值…

data.describe()

---

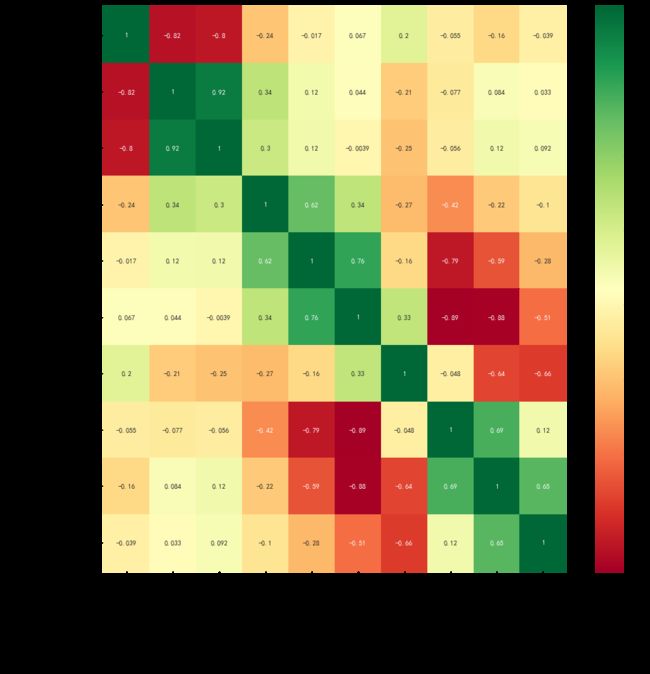
数据相关性

corr = abs(data.corr())
corr['Number of  reported results'].sort_values(ascending=False)

Number in hard mode 0.922252
Contest number 0.821787
1 try 0.342183
4 tries 0.211693
2 tries 0.118527
6 tries 0.084180
5 tries 0.077308
3 tries 0.043624
7 or more tries (X) 0.033079

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

• 相关系数：
  • 0.8-1.0 极强相关
  • 0.6-0.8 强相关
  • 0.4-0.6 中等程度相关
  • 0.2-0.4 弱相关
  • 0.0-0.2 极弱相关或无相关

皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。相关系数的强弱仅仅看系数的大小是不够的。

一般来说，取绝对值后，0-0.09为没有相关性，0.3-弱，0.1-0.3为弱相关，0.3-0.5为中等相关，0.5-1.0为强相关。但是，往往你还需要做显著性差异检验，即t-test，来检验两组数据是否显著相关，这在SPSS里面会自动计算的。

plt.figure(figsize=(15,15))
g=sns.heatmap(data.corr(),cmap='RdYlGn',annot=True)
plt.show()

---

回归预测模型——XGBoost

XGBoost 最早的雏形出现在 2014 年，当时由 陈天奇 读博期间负责的研究项目中。后经开源，逐渐发展成一个支持 C++，Java，Python，R 和 Julia 语言的成熟框架。XGBoost 是 Extreme Gradient Boosting 的缩写，其中的 Gradient Boosting 实际上就是梯度提升算法。

Gradient Boosting 的名字实际上由 2 部分组成：Gradient Descent + Boosting。首先需要搞清楚什么是 Boosting。Boosting 含义正如字面意思「提升」，通过对弱学习器进行改进，得到强学习器的过程，也就是提升过程。弱学习器是非常简单的模型，复杂度低，训练简单，不容易过拟合。
这些模型往往也就比随意乱猜好一些，例如只有一层深度的决策树。那么，将选择的弱学习器称为基学习器，在此基础上进行组合得到改进之后的学习器。

评价指标

需要一个评价指标，对于回归问题常选择 MSE 均方误差来进行评估。公式如下：

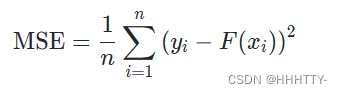
基于公式计算 MSE 的值：

# 计算 MSE 值
np.square(np.subtract(y, y_)).mean()

XGBoost 框架使用

先执行下面命令进行安装。

pip install xgboost  # 安装 

回归调用 XGBRegressor() 接口。

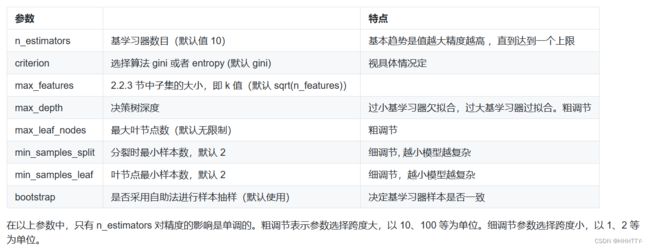
使用 XGBoost 建模。XGBoost 的分类器方法为 XGBRegressor。参数非常多，我们看一下常用的几个：

• max_depth – 基学习器的最大树深度。
• learning_rate – Boosting 学习率。
• n_estimators –决策树的数量。
• gamma – 惩罚项系数，指定节点分裂所需的最小损失函数下降值。
• booster – 指定提升算法：gbtree,gblinear or dart。
• n_jobs – 指定多线程数量。
• reg_alpha – L1 正则权重。
• reg_lambda – L2 正则权重。
• scale_pos_weight – 正负权重平衡。
• random_state – 随机数种子。

以默认参数来初始化模型。

• 调用 XGBRegressor() 训练模型及评估。

import xgboost as xgb

model_r = xgb.XGBRegressor()

---

划分数据集，80% 训练数据和 20% 测试数据

X = data.drop(labels='Number of  reported results', axis=1)
y = data['Number of  reported results']  # 目标值

from sklearn.model_selection import train_test_split

# 划分数据集，80% 训练数据和 20% 测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

---

使用训练数据训练

• 使用训练数据训练
• 使用测试数据计算 R^2 评估指标

model_r.fit(X_train, y_train)  # 使用训练数据训练
model_r.score(X_test, y_test)  # 使用测试数据计算 R^2 评估指标

参数

XGBClassifier 和 XGBRegressor 中都存在一个参数 objective。

• 解决分类问题时，默认选择了 objective=‘binary:logistic’，而回归问题默认选择了 objective=‘reg:linear’。
• 从字面意思你应该能发现，这是一个指定学习器完成哪种类型任务的参数，通常称为目标参数。

那么，该参数在解决回归问题时一般为 reg:linear（即将更名为：reg:squarederror） 和 reg:logistic，分别代表线性回归和逻辑回归。

---

绘制决策树

XGBoost 提供了 xgb.plot_tree 方法，可以将模型训练好之后的决策子树绘制出来。

• 使用时，只需要传入模型和子树的序号即可，想画哪颗就画哪颗。

安装 graphviz 包

# 安装 graphviz 包
!pip install graphviz

from matplotlib import pyplot as plt
from matplotlib.pylab import rcParams
%matplotlib inline

# 设置图像大小
rcParams['figure.figsize'] = [50, 10]

xgb.plot_tree(model_t, num_trees=1)

交叉验证

如何使用 XGBoost 进行交叉验证。

交叉验证是机器学习中快速评估模型的重要方法。

• 可以将数据集划分为 N 个子集，使用其中的 N-1 个集合训练模型，最后在剩余的 1 个子集上进行评估。

依次轮询，最后求出 N 次评估的平均指标，作为该模型的最终评价结果。

• XGBoost 提供了 xgb.cv 方法用于完成交叉验证过程。

所以，交叉验证无需再单独划分训练和测试集，直接使用完整数据集即可。

# 依次传入特征和目标值

data_d = xgb.DMatrix(data=X, label=y)

xgb.cv(dtrain=data_d , params={'objective': 'reg:squarederror'}, nfold=5, as_pandas=True)

上方参数中，

• dtrain 传入数据集，params 为模型自定义参数，
• nfold 为交叉验证划分的 N 个子集，
• as_pandas 则表示最终以DataFrame 样式输出。

默认情况下，XGBoost 会执行 Boosting 迭代 10 次，所以你可以看到 10 行输出。

• 当然，你可以修改 num_boost_round 参数，自定义最大迭代次数。

---

问题二

• 对于未来日期的给定未来解决方案词，
  • 开发一个模型，使您能够预测报告结果的分布。
  • 换句话说，预测未来日期 (1, 2, 3, 4, 5, 6, X) 的相关百分比。
  • 哪些不确定性与您的模型和预测相关？
  • 举一个你对 2023 年 3 月 1 日 EERIE 这个词的预测的具体例子。
  • 你对你的模型的预测有多自信？

元音字母有：a、e、i、o、u五个，其余为辅音字母。

辅音字母为：b、c、d、f、g、h、j、k、l、m、n、p、q、r、s、t、v、w、x、y、z。

Vowel = ['a','e','i','o','u'] 
Consonant = list(set(small).difference(set(Vowel)))
def count_Vowel(s):
    c = 0
    for i in range(len(s)):
        if s[i] in Vowel:
            c+=1
    return c
def count_Consonant(s):
    c = 0
    for i in range(len(s)):
        if s[i] in Consonant:
            c+=1
    return c

df['Vowel_fre'] = df['Word'].apply(lambda x:count_Vowel(x)) 
df['Consonant_fre'] = df['Word'].apply(lambda x:count_Consonant(x))

时间特征转换

df["year"] = df.index.year

df["quarter"] = df.index.quarter

df["month"] = df.index.month

df["week"] = df.index.week

df["weekday"] = df.index.weekday

数据标准化

数据的标准化，是通过一定的数学变换方式，将原始数据按照一定的比例进行转换，使之落入到一个小的特定区间内，例如0-1或-1-1的区间内

• 消除不同变量之间性质、量纲、数量级等特征属性的差异，将其转化为一个无量纲的相对数值，
• 也就是标准化数值，使各指标的数值都处于同一个数量级别上，
• 从而便于不同单位或数量级的指标能够进行综合分析和比较。

from sklearn.preprocessing import StandardScaler

# 标准化
std = StandardScaler()
X1 = std .fit_transform(X)

集成学习——随机森林

集成学习就是构建并结合多个个体学习器（称为基学习器）来完成学习任务。举一个例子。下表中 √ 表示分类正确，× 表示分类错误。

随机森林

随机森林以决策树为基学习器。但是属性选择与决策树不同。

• 随机森林中，基决策树学习器在每个节点上，从该节点的属性集合中随机选择包含 K 个属性的子集，再从子集中选择最优属性用于划分。
• 这就满足 “好而不同” 的条件。随机森林计算开销小，是现在机器学习算法当中水平较高的算法。

sklearn 参数调节

交叉验证法调参

我们首先调节：n_estimators，max_depth。

• 首先观察特征数目，这决定了 max_depth 等参数的范围。
• 然后使用交叉验证法调参。
  得到最优参数 n_estimators=100，max_depth=10。

def para_tune(para, X, y): #
    clf = RandomForestClassifier(n_estimators=para) # n_estimators 设置为 para
    score = np.mean(cross_val_score(clf, X, y, scoring='accuracy'))
    return score

def accurate_curve(para_range, X, y, title):
    score = []
    for para in para_range:
        score.append(para_tune(para, X, y))
    plt.figure()
    plt.title(title)
    plt.xlabel('Paramters')
    plt.ylabel('Score')
    plt.grid()
    plt.plot(para_range, score, 'o-')
    return plt

g = accurate_curve([2, 10, 50, 100, 150], X, y, 'n_estimator tuning')

def para_tune(para, X, y):
    clf = RandomForestClassifier(n_estimators=300, max_depth=para)
    score = np.mean(cross_val_score(clf, X, y, scoring='accuracy'))
    return score

def accurate_curve(para_range, X, y, title):
    score = []
    for para in para_range:
        score.append(para_tune(para, X, y))
    plt.figure()
    plt.title(title)
    plt.xlabel('Paramters')
    plt.ylabel('Score')
    plt.grid()
    plt.plot(para_range, score, 'o-')
    return plt

g = accurate_curve([2, 10, 20, 30, 40], X, y, 'max_depth tuning')

---

scikit-learn 自动调参函数 GridSearchCV

from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import learning_curve

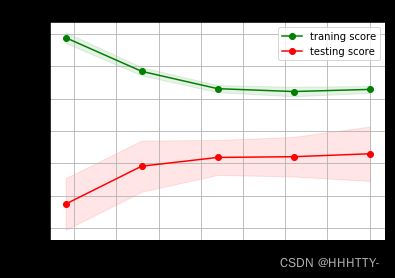
def plot_learning_curve(estimator, title, X, y, cv=10,
                        train_sizes=np.linspace(.1, 1.0, 5)):
    plt.figure()
    plt.title(title) # 设置图的 title
    plt.xlabel('Training examples') # 横坐标
    plt.ylabel('Score') # 纵坐标
    train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv,
                                                            train_sizes=train_sizes) 
    train_scores_mean = np.mean(train_scores, axis=1) # 计算平均值
    train_scores_std = np.std(train_scores, axis=1) # 计算标准差
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    plt.grid() # 设置背景的网格

    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std,
                     alpha=0.1, color='g') # 设置颜色
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std,
                     alpha=0.1, color='r')
    plt.plot(train_sizes, train_scores_mean, 'o-', color='g',
             label='traning score') # 绘制训练精度曲线
    plt.plot(train_sizes, test_scores_mean, 'o-', color='r',
             label='testing score') # 绘制测试精度曲线
    plt.legend(loc='best')
    return plt

clf = RandomForestClassifier()
para_grid = {'max_depth': [10], 'n_estimators': [100], 'max_features': [1, 5, 10], 'criterion': ['gini', 'entropy'],
             'min_samples_split': [2, 5, 10], 'min_samples_leaf': [1, 5, 10]}#对以上参数进行网格搜索
gs = GridSearchCV(clf, param_grid=para_grid, cv=3, scoring='accuracy')
gs.fit(X, y)
gs_best = gs.best_estimator_ #选择出最优的学习器
gs.best_score_ #最优学习器的精度

g = plot_learning_curve(gs_best, 'RFC', X, y)#调用实验2中定义的 plot_learning_curve 绘制学习曲线

---

问题三

• 开发并总结一个模型来按难度对解决方案单词进行分类。
  • 识别与每个分类关联的给定词的属性。
  • 使用您的模型，EERIE 这个词有多难？
  • 讨论分类模型的准确性。

Kmeans 聚类算法

算法思想

通过不断的迭代来寻找 k 值，形成一种划分方式，使得用这 k 个类簇的均值来代表相应各类样本时所得的总体误差最小。

• 同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
• k-means 算法的基础是最小误差平方和准则， 其函数是：
  
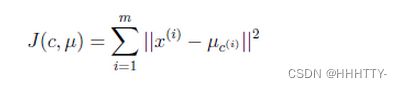
  上式中，μc(i) 表示第 i 个聚类的均值。
• 划分到各类簇内的样本越相似，其与该类均值间的误差平方越小，
• 然后对所有类计算所得到的误差平方再次累加求和，
• 即我们希望 J 值越小越好。

算法实现步骤

k-means 算法是将样本聚类成 k 个簇中心，这里的 k 值是我们给定的，也就是我们希望把数据分成几个类别。

具体算法描述如下：

1. 为需要聚类的数据，随机选取 k 个聚类质心点；
2. 求每个点到聚类质心点的距离，计算其应该属于的类，迭代直到收敛于某个值。

# 导入 KMeans 估计器
from sklearn.cluster import KMeans
est = KMeans(n_clusters=4)  # 选择聚为 4 类
est.fit(X)
y_kmeans = est.predict(X)  # 预测类别，输出为含0、1、2、3数字的数组

# 为预测结果上色并可视化
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = est.cluster_centers_  # 找出中心
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)  # 绘制中心点

K均值算法：期望最大化

K-Means 是使用期望最大化方法得出结果的算法。期望最大化可解释成两步，其工作原理如下：
1.猜测一些簇中心点。
2.重复直至收敛。

期望步骤（E-step）：将点分配至离其最近的簇中心点。
最大化步骤（M-step）：将簇中心点设置为所有点坐标的平均值。

from sklearn.metrics import pairwise_distances_argmin  # 最小距离函数
import numpy as np


def find_clusters(X, n_clusters, rseed=2):
    # 1.随机选择簇中心点
    rng = np.random.RandomState(rseed)
    i = rng.permutation(X.shape[0])[:n_clusters]
    centers = X[i]
    while True:
        # 2a.基于最近的中心指定标签
        labels = pairwise_distances_argmin(X, centers)
        # 2b.根据点的平均值找到新的中心
        new_centers = np.array([X[labels == i].mean(0)
                                for i in range(n_clusters)])
        # 2c.确认收敛
        if np.all(centers == new_centers):
            break
        centers = new_centers
    return centers, labels


centers, labels = find_clusters(X, 4)
plt.scatter(X[:, 0], X[:, 1], c=labels,
            s=50, cmap='viridis')  # 绘制聚类结果