代码随想录训练营第23天|LeetCode 669. 修剪二叉搜索树 、108.将有序数组转换为二叉搜索树 、 538.把二叉搜索树转换为累加树
参考
代码随想录
题目一:LeetCode 669.修剪二叉树
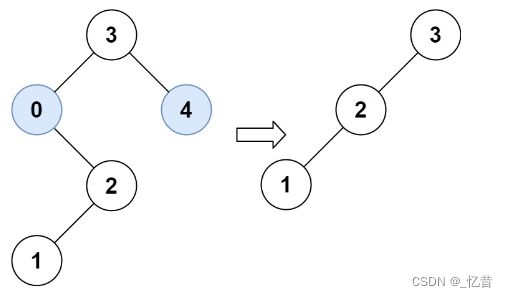
这个题的难点在于理解怎么修改二叉树,如上题,如果区间为[1,3],那么节点0不满足,此时应该将节点0的右节点作为节点0父节点的新的左节点,而将节点0及其左子树删除;另外,如果某个节点的值大于high,则将该节点及其右子树删除,然后将该节点左子树作为该节点父节点的新的右子树。这是理解本题解法的关键,这样做还是由二叉搜索树的性质决定的。
- 确定递归函数的参数和返回值
参数:根节点root,左右区间low和high
返回值:返回修剪后的节点(也可能每变化),每一层返回有一个节点作为上一层调用时的节点的左节点或者右节点
TreeNode* trimBST(TreeNode* root, int low, int high)
- 确定递归终止条件:当遇到空节点时时候返回空即可
if(root == nullptr) return nullptr;
- 确定单层递归逻辑:单层递归的处理就是前面所描述的,如果root->val < low,则将root节点的右子树作为root节点父节点的新的左节点,然后删除root节点及其左子树;如果root->val > high,则将root节点的左子树作为root节点父节点的新的右子树,然后删除root节点及其右子树。
if(root->val < low) return trimBST(root->right,low,high);
if(root->val > high) return trimBST(root->left,low,high);
root->left = trimBST(root->left,low,high);
root->right = trimBST(root->right,low,high);
return root;
完整的代码实现如下:
class Solution {
public:
TreeNode* pre = nullptr;
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root == nullptr) return nullptr;
if(root->val < low) return trimBST(root->right,low,high);
if(root->val > high) return trimBST(root->left,low,high);
root->left = trimBST(root->left,low,high);
root->right = trimBST(root->right,low,high);
return root;
}
};
上面的代码只是将不符合要求的节点移除,并没有真正的删除。
题目二:LeetCode 108.将有序数组转换为二叉搜索树
以数组中间点为分割点(偶数是中间两个点任取一个)分割数组,然后递归左右区间。
- 确定递归函数的参数和返回值
参数:数组和数组区间的左右指针,传入的区间为左闭右闭
返回值:当前节点的子节点
TreeNode* traversal(vector<int>& nums,int left,int right);
- 确定递归终止条件:因为传入的区间为左闭右闭,所以当left > right的时候区间里没有数据,递归结束
if(left > right) return nullptr;
- 确定单层递归逻辑:递归左右区间,用左区间数据生成左节点,右区间数据生成右节点
int mid = (right + left) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
完整的代码实现如下:
class Solution {
public:
TreeNode* traversal(vector<int>& nums,int left,int right)
{
if(left > right) return nullptr;
int mid = (right + left) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return traversal(nums,0,nums.size()-1);
}
};
题目三:LeetCode 538.把二叉搜索树转换为累加树
这个题理解了题目意思之后就很好做了,按照题意,需要以右中左的遍历顺序,因为二叉搜索树中,右节点数值最大,中间节点次之,左节点最小,因此只需要以右中左的顺序遍历二叉树,并用一个全局变量来记录累加值,更新当前节点的数值即可。
- 确定递归函数的参数和返回值:
参数:根节点
返回值:无
void traversal(TreeNode* root);
- 确定单层递归逻辑:当遇到空节点的时候结束递归
if(root == nullptr) return;
- 确定单层递归逻辑:当前节点的新值是累加值加上原来的值,然后将累加值更新为当前节点的新值
traversal(root->right); //右
root->val += sum; //中
sum = root->val;
traversal(root->left); //左
完整的代码实现如下:
class Solution {
public:
int sum = 0;
void traversal(TreeNode* root)
{
if(root == nullptr) return;
traversal(root->right); //右
root->val += sum; //中
sum = root->val;
traversal(root->left); //左
}
TreeNode* convertBST(TreeNode* root) {
traversal(root);
return root;
}
};