1.30学习总结5
栈
1、栈的概念
栈是限定仅在表尾进行插入和删除操作的线性表。把允许去插入和删除的一端叫做栈顶,另一端称为栈底,不含任何元素的栈称为空栈,这又称为后进先出(Last In First Out,LIFO)的线性表。栈的插入操作称为进栈(Push),删除操作称为出栈(Pop)。栈的另一个重要特性是只能访问栈顶元素,不能直接访问其他位置的元素。
1.1、栈的特点
- 先入栈的元素会放在栈的底部。
- 取出元素的时候,先取出顶部元素。
- 栈的大小是有限的,如果栈满了不能放元素,栈空不能取出元素。
1.2、栈的主要操作
- 进栈(Push):将元素插入到栈顶。
- 出栈(Pop):将栈顶元素删除并返回。
- 获取栈顶元素(Top):返回栈顶元素的值,但不对栈做任何修改。
- 判空(isEmpty):判断栈是否为空栈。
- 获取栈的大小(getSize):返回栈中元素的个数。
1.3、栈的应用场景
- 函数调用:每次调用函数时,函数的返回地址、参数和局部变量都会被压入栈中,函数执行完后再出栈恢复现场。
- 浏览器的后退功能:浏览器可以使用栈来记录用户访问的网页,每次后退操作就是将最近访问的网页从栈中弹出。
表达式求值:在编译器和计算器中,栈可以用来实现中缀表达式转后缀表达式,以及后缀表达式的求值。
2、栈的顺序存储结构
2.1、顺序栈
采用顺序存储的栈称为顺序栈,利用一组地址连续的存储单元存放从栈底到栈顶的元素,同时附设一个指针(top)指示当前栈顶的位置。
2.2、栈的顺序存储
栈的顺序存储指的是使用数组来实现栈的存储结构。栈的顺序存储有以下特点:
- 使用数组作为底层数据结构,可以通过下标直接访问栈中的元素。
- 栈的底层数组有一个固定的大小,称为栈的容量。
- 通过一个变量top来表示栈顶元素在数组中的位置,初始时top为-1。
- 当有元素入栈时,将top的值加1,并将元素放入数组中的top位置。
- 当有元素出栈时,先取出数组中的top位置的元素,然后将top的值减1。
- 栈满的条件是top等于栈的容量减1,栈空的条件是top等于-1。
若现在有一个栈,StackSize是5,则栈的普通情况、空栈、满栈的情况分别如下图所示:
栈的顺序存储结构可描述为:
#define MAXSIZE 50 //定义栈中元素的最大个数
typedef struct
{
int data[MAXSIZE];
int top; //用于栈顶指针
}SqStack;
2.3、顺序栈的操作
2.3.1、初始化
void InitStack(SqStack *s)
{
s->top=-1; //栈顶指针初始化为-1,表示栈为空
}2.3.2、判栈空
如果栈为空,则返回0;如果栈不为空,则返回-1。
int StackEmpty(SqStack *s)
{
if(s->top==-1)
return 0; //栈空
else return -1;
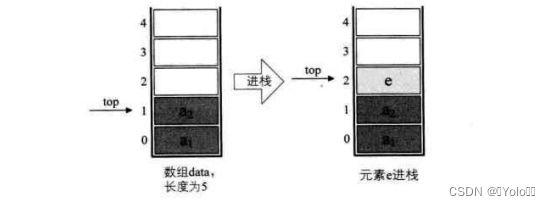
}2.3.3、进栈
首先判断栈是否已满,如果栈满了,则返回-1;如若没有满,则在栈顶中插入e元素,并返回0。
int Push(SqStack *s, ElemType e)
{
//满栈
if(s->top==MAXSIZE-1)
return -1;
s->top++; //栈顶指针加1
s->data[s->top]=e; //将新插入元素赋值给栈顶空间
return 0;
}2.3.4、出栈
首先判断栈是否为空,如果已经为空,则返回-1;如果不为空,则取得栈顶元素,并返回0。
int Pop(SqStack *s, ElemType *e)
{
if(s->top==-1)
return -1; //栈空
*e=s->data[s->top]; //将要删除的栈顶元素赋值给e
s->top--; //栈顶指针减1
return 0;
}2.3.5、读栈顶元素
首先判断栈是否为空,如果为空,则返回-1;如果不为空,则读取栈顶元素,并返回0。
int GetTop(SqStack *s, ElemType *e)
{
if(s->top==-1) //栈空
return -1;
*e=s->data[s->top]; //记录栈顶元素
return 0;
}2.3.6、实例
int main()
{
Stack s;
initStack(&stack);
push(&s, 1);
push(&s, 2);
push(&s, 3);
printf("Stack top: %d\n", GetTop(&s));
printf("Stack pop: %d\n", Pop(&s));
printf("Stack pop: %d\n", Pop(&s));
printf("Stack top: %d\n", GetTop(&s));
return 0;
}
Stack top: 3
Stack pop: 3
Stack pop: 2
Stack top: 1
3、共享栈
3.1、定义
利用栈底位置相对不变的特征,可让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸。
共享栈的数据结构可以描述为:
#define MAXSIZE 50
typedef struct
{
int data[MAXSIZE];
int top1; // 第一个栈的栈顶指针
int top2; // 第二个栈的栈顶指针
}SharedStack;共享栈的判断条件进行说明。
栈空条件:1号栈【top1==-1】;1号栈【top2==MAXSIZE】
栈满条件:top2-top1=1
3.2、共享栈的操作
3.2.1、初始化
void InitStack(SharedStack *s)
{
s->top1=-1; //初始化1号栈顶指针
s->top2=MAXSIZE; //初始化2号栈顶指针
}
3.2.2、判栈空
1号栈为空,则top1==-1;若2号栈为空,则top2==MaxSize;那么若两个栈均为空则返回0;如果栈不为空,则返回-1。
int StackEmpty(SqStack* s)
{
if(s->top1==-1&&s->top2==MaxSize)
return 0;
else
return -1;
}
3.2.3、进栈
int Push(SqStack*s,ElemType x,int n)
{
if(s->top2-s->top2==1)
{
printf("The stack is full!\n");
return -1;
}
switch(n)
{
case 1:s->data[++s->top1]=x;break;
case 2:s->data[--s->top2]=x;break;
}
return 0;
}
3.2.4、出栈
int Pop(SqStack *s, ElemType* x,int n)
{
switch(n)
{
case 1:
if(s->top1==-1)
printf("The stack1 is empty!\n");
else *x=s->data[s->top1--];
break;
case 2:
if(s->top2==MaxSize)
printf("The stack2 is empty!\n");
else *x=s->data[s->top2++];
break;
}
return 0;
}4、栈的链式存储结构
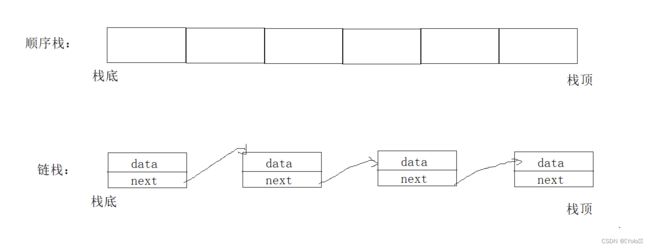
4.1、链栈
采用链式存储的栈称为链栈,通常采用单链表实现。链栈可以动态地增加和删除元素,不受容量限制,不存在栈满上溢的情况,但相应地也会导致指针的频繁变化。
4.2、栈的链式存储
链栈的结构可描述为:
//构造结点
typedef struct StackNode
{
int data;
struct StackNode *next;
}LinkStackPrt;
//构造链栈
typedef struct LinkStack
{
LinkStackPrt *top;
int count;
}LinkStack;
4.3、共享栈的操作
4.3.1、初始化
将栈顶指针置为空:
void initStack(Stack* s)
{
s->top=NULL;
}
4.3.2、进栈
操作时,创建一个新的节点,将数据赋值给新节点的数据域,然后将新节点的指针域指向当前栈顶节点,并将栈顶指针指向新节点:
void push(LinkStack* s, int data)
{
LinkStackPrt* newNode=(LinkStackPrt*)malloc(sizeof(LinkStackPrt));
newNode->data=data;
newNode->next=s->top;
s->top=newNode;
}
4.3.3、出栈
操作时,首先判断栈是否为空,如果为空则无法出栈,否则将栈顶指针指向当前栈顶节点的下一个节点,并释放当前栈顶节点的内存空间:
int pop(LinkStack* s)
{
if (s->top==NULL)
{
printf("Stack is empty.\n");
return -1;
}//栈空
int data=s->top->data;
LinkStackPrt* temp=s->top;//将栈顶结点赋值给temp
s->top=s->top->next;//使得栈顶指针下移一位,指向后一结点
free(temp); //释放temp
return data;
}
4.3.4、读取栈顶元素
int GetTop(LinkStack* s)
{
if (s->top==NULL)
{
printf("Stack is empty.\n");
return -1;
}
return s->top->data;
}
5、应用-四则运算表达式求值
5.1、后缀表达式计算结果
中缀表达式不仅依赖运算符的优先级,而且还要处理括号。后缀表达式的运算符在操作数后面,在后缀表达式中已考虑了运算符的优先级,没有括号,只有操作数和运算符。
例如中缀表达式A+B∗(C−D)−E/F所对应的后缀表达式为 ABCD-*+EF/-。
计算规则
从左到右遍历表达式的每个数字和符号,遇到是数字就进栈,遇到是符号,就将处于栈顶两个数字出栈,进项运算,运算结果进栈,一直到最终获得结果。
5.2、中缀转后缀表达式
把平时所用的标准四则运算表达式,即a+b−a∗((c+d)/e−f)+g等叫做中缀表达式。因为所有的运算符号都在两数字的中间,现在我们的问题就是中缀到后缀的转化。
转化规则
从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
5.3、求值
要想让计算机具有处理我们通常的标准(中缀)表达式的能力,最重要的两步:
- 将中缀表达式转化为后缀表达式(栈用来进出运算的符号)。
- 将后缀表达式进行运算得出结果(栈用来进出运算的数字)。