算法day4

算法day4

• 283移动0
• 11 盛水最多的容器
• 24 两两交换链表中的结点
• 19 删除链表中的倒数第N个结点
• 面试题02.07.链表相交
• 环形链表

---

283 移动0

拿到这个题的想法：1.重新开个数组，然后遍历原数组构造新数组。2.双指针构造，fast用于遍历，slow用于赋值。3.还有个暴力解法，遇到0我就后往前覆盖，并统计0的个数count，这样一直遍历到最后，把数组后面count个元素全赋值为0。
然后我的选择了法二，法一不让用，法3一看就是两个for循环O(n^2)了。

双指针

func moveZeroes(nums []int)  {
    slow:=0
    for fast:=0;fast<len(nums);fast++{
        if nums[fast]!=0{
            nums[slow]=nums[fast]
            slow++
        }
    }

    for slow<len(nums){
        nums[slow] = 0
        slow++
    }
}

这个版本是当时独立写的版本。就是想到啥写啥。
还有一个题解版本，这个版本也是双指针，但是显然就处理的非常优雅。这个版本的处理方式就不是赋值，而是交换，直接在这个双指针的过程把0交换到了数组尾部。

func moveZeroes(nums []int)  {
    fast,slow:=0,0
    for fast<len(nums){
        if nums[fast]!=0{
            nums[slow],nums[fast] = nums[fast],nums[slow]
            slow++
        }
        fast++
    }
}

我总结了如何才能想到该这么干。要点是基于交换来构造。
所以想到“交换”是一个关键点。

盛最多水的容器

只能说自己太菜了，第一时间就只想到暴力。暴力的思路就是两个for循环，直接把所有可能遍历出来取最大值。然后一提交就爆时间了。下面是我的这个暴力解，看看就行了。

func max(a int,b int)int{
    if a>b{
        return a
    }else{
        return b
    }
}

func min(a int,b int)int{
    if a<b{
        return a
    }else{
        return b
    }
}

func maxArea(height []int) int {
    m :=0
    for i:=0;i<len(height);i++{
        for j:=i+1;j<len(height);j++{
            temph :=min(height[i],height[j])
            templ :=j-i
            tempm := temph*templ
            m=max(m,tempm)
        }
    }

    return m
}

能积累到的知识就是，go语言没有min和max这样的库函数，要自己写。

---

看了题解后的解法：用的是双指针，我当时在做的时候也想到了，但是我就觉得不太合理，因为双指针的做法就是直接往内收缩。这就让我对有些例子产生疑问，我觉得这样不一定吧。
然后我就看到了一个大佬的题解，并且做了正确性的证明。
我看了这个视频https://www.bilibili.com/video/BV1mJ411M7gE/?spm_id_from=333.337.search-card.all.click&vd_source=49ceaf0b94868131c32ccefb11e30e8f。再结合这个大佬的题解https://leetcode.cn/u/jyd/搞懂这个题的。

双指针解法

首先这个双指针，一个在最左一个在最右边，这样取的原因我认为就是贪心的思想。尽量保证公式里面的元素尽可能地大。这样就保证了底边最大。

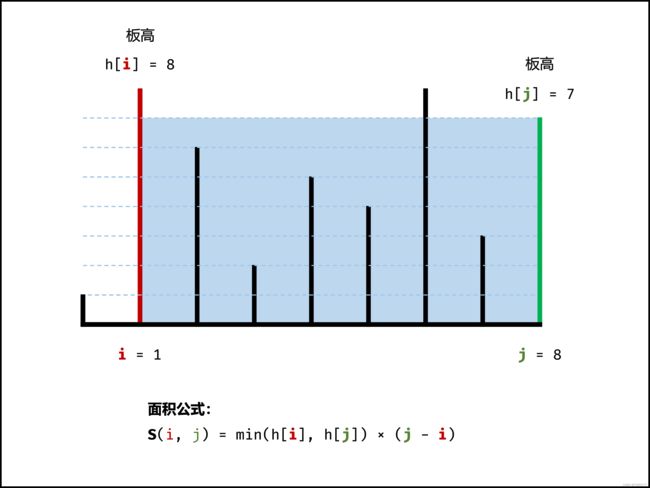
这个公式我在暴力解的时候也推出来了，这个只要用过暴力解这个公式是不难想到的。
这个解法最精髓的一句话：水槽的实际高度由两板中的短板决定。
这句话也可以证明：
如果向内移动长版，水槽的短板min(h[i],h[j])可能变小，也有可能不变。但是这个水槽的面积因为底变短了，所以一定变小
如果向内移动短板，水槽的短板min(h[i],h[j])可能变大也有可能变小还有可能增大还有可能不变，但是可以推出，面积由增大的可能。
综上，按照题目的要求，我们要最大的面积，那可以推出肯定是短板向内收缩。
经过上面地分析：代码的写法就有了，指针初始化：分别取在最左和最右。每轮循环短板向内收缩，知道left=right，这样面积为0了。在这个迭代的过程中即可获得最大值。

这个是我写的双指针版本：

func max(a int,b int)int{
    if a>b{
        return a
    }else{
        return b
    }
}

func min(a int,b int)int{
    if a<b{
        return a
    }else{
        return b
    }
}

func maxArea(height []int) int {
    left,right:=0,len(height)-1
    m:=0
    for left != right{
        tempm:= min(height[left],height[right])*(right-left)
        m = max(tempm,m)
        if height[left]<=height[right]{
            left++
        }else{
            right--
        }
    }
    return m
}

和上面说的逻辑一模一样照着写的。

总结：拿到这个题，双指针这个写法我看了很多题解，上来就直接往内收缩，这就让我觉得这也不一定能拿到最大值，但是经过上面的推理之后，我才懂这个过程是合理的。是一种贪心的思想。我是站在s = min(height[left],height[right])*(right-left)这个角度上用贪心的思想理解的。根据贪心的思想，初始化的值很容易就能想到left = 0,right=len(height)-1。这样保证了长度是最长的，接下来按照贪心的思想，就是我的下一步要往最优选择去靠，上面推理移动长版必定变小，因此移动短板才符合。

---

两两交换链表中的结点

拿到这个题，还是被自己菜笑了，就是写不出，要是只要这个结果，那毫无疑问我直接遍历交换结点值就写完了。但是不动结点值的做法我是写不出的。这也是考察的重点。
本题就是在考察直接交换结点，而不是交换数值。
做法关键：这三个问题能想出来这个题就能做的出来。

1.要不要dummyhead。
2.结点怎么交换。
3.循环什么时候退出。

回答：
1.要dummyhead，这里我一开始想不明白这个交换，就是没想到这个dummyhead作用是什么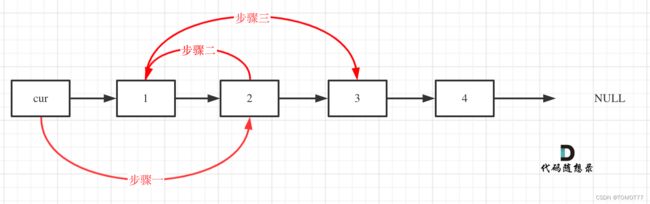
后来想清楚了，如果我不要这个dummyhead一方面是我写这个代码会比较复杂，比如我就要特殊的处理这个头结点，一般情况下这个头结点将会是第二个结点，而在特殊的情况下，比如只有一个结点，或者是没有结点这种，那我又要做一个特判，而且写一般情况下，我要考虑结点是奇数还是偶数，这又会多一个特判。这就会导致，如果我不做dummyhead使得操作统一化处理，那么这个代码就会变得很麻烦。但是如果我用到了dummyhead，那我就根本不用考虑一些极端的情况，因为dummyhead的作用就是使得操作统一。当然我感觉不用那也是可以的，但是不如用dummyhead的好写。
所以这里我总结了一下：平常最好还是用dummyhead，原因就是可以少写特判，尤其是针对极端的例子像是没有结点或者只有一个结点这种。统一化处理一步到位。
2.从上面的图就可以知道步骤是什么，但是我这里还有其他的思考，我这样连行不行：cur->2,1->3,2->1，答案是可以的，这里我的总结是：如果想到这种连法，自己画图试着写代码出来判断一下这样连会不会导致链表断裂。不断裂说明写的就没毛病。还有就是从上图发现，我要操作1，2我就必须要找1，2的前一个指针，这样我才能完成这样的交换操作。所以下次我操作3，4，那显然我的cur就要有这样的操作，cur指2的那个地方。
3.按照上面这样的操作方式，我要操作后两个元素，那就要找前一个元素。按照这样的性质然后这个过程往后推，就知道循环停止在那里。这里的处理我只能说，当时我真没想到可以这样处理。我本来还打算遍历结点统计个数，然后分奇数偶数来写，根本没必要。直接看这个终止条件。cur.next!=nil&&cur.next.next!=nil 带入这个过程就可以理解清楚：
奇数：dummyhead->1->2->3->4->5->nil，这个例子我显然最后一个元素不需要交换，此时也停下来了，那此时什么条件导致循环停止的，假设此时如果想交换5和5后的元素，cur此时指向的就是4，这样操作规则。那么此时cur.next.nextnil
偶数：dummyhead->1->2->3->4->nil
按上面的过程，cur.nextnil
极端情况：
dummyhead->1->nil
dummyhead->nil
我一开始cur指向dummyhead同样满足上面的判断情况。

所以循环的退出条件就是cur.next!=nil&&cur.next.next!=nil
这个条件还有一个非常重要的细节：这个并列条件能不能交换次序，答案是不能，如果交换次序，在偶数的情况，由于cur.next=nil了，这里先进行cur.next.next与nil的判断，那这里就空指针异常了。这是个很细节的点。我当时压根就没想到这么多。

把这些弄懂了，我觉得这个代码是很好写出来的，关于向后移动，这个直接temp存就行了，缺什么就存什么。

版本一

这种交换方式是图中的交换方式

func swapPairs(head *ListNode) *ListNode {
    dummyhead := &ListNode{}
    dummyhead.Next=head
    cur:=dummyhead
    for cur.Next!=nil&&cur.Next.Next!=nil{
    	//向后移动的临时指针
        temp1:=cur.Next
        temp2:=cur.Next.Next.Next
		//交换操作
        cur.Next=cur.Next.Next
        cur.Next.Next=temp1
        cur.Next.Next.Next=temp2
        //向后移动
        cur = temp1
    }

    return dummyhead.Next
}

版本二

这种交换方式是cur->2,1->3,2->1这种

func swapPairs(head *ListNode) *ListNode {
    dummyhead := &ListNode{}
    dummyhead.Next=head
    cur:=dummyhead
    for cur.Next!=nil&&cur.Next.Next!=nil{
        temp1:=cur.Next
        temp2:=cur.Next.Next.Next

        cur.Next=cur.Next.Next
        temp1.Next=temp2
        cur.Next.Next=temp1
        cur = temp1

        
    }

    return dummyhead.Next
}

总结：两种交换方式都是可行的。时间复杂度o(n)

我写的时候还有一个问题，就是这个cur后移的问题，要注意cur后移应该是移动到temp1，如果直接cur=cur.next就错了。因为这里发送了交换操作，要小心一点。

另外这个题也是有递归版本的，但是我觉得递归费空间。

---

19 删除链表中的倒数第N个结点

这个题目我感觉就简单多了，拿到题目我有两个思路：
1.先遍历统计个数，然后再遍历一次进行删除，这种慢了点。
2.双指针，让快的先走N步，然后慢的和快的一起走，这种应该是比较好的解法,时间是o(n)，空间o(1)
我就写了法二
这个思路：dummyhead->1->2->3->4->null，fast和slow都先指向dummyhead，因为删除操作你要找要删除的前一个元素才能实现删除操作。让fast先走n步，循环当fast.Next==null了就停下来。此时slow就在要删除的元素的前面，直接进行删除操作即可。

func removeNthFromEnd(head *ListNode, n int) *ListNode {
    dummyhead:=&ListNode{}
    dummyhead.Next=head
    fast,slow:=dummyhead,dummyhead

    for i:=0;i<n;i++{
        fast=fast.Next
    }
    for fast.Next!=nil{
        slow=slow.Next
        fast=fast.Next
    }

    slow.Next=slow.Next.Next
    
    return dummyhead.Next
    
}

这个题就没什么问题一次过。但是这个过程我建议做的时候与其去想之前怎么做的，不如直接自己模拟一下。背答案我觉得就不太好。思路可以记一记。

---

面试题02.07.链表相交

拿到第一感觉，感觉是双指针，但是写不出来。如果硬座我只能想到链表转数组，然后两个for直解暴力枚举，然后转链表，但是题目要求不能这么搞，他并不是要求数值相等，而是指针相等。（被自己菜麻了）。

看了题解之后的想法：很多题解只说了要这么做，没说为什么，这里我就写了几个我看得懂的解法
解法一：双指针
这个解法是我目前可以解释得懂的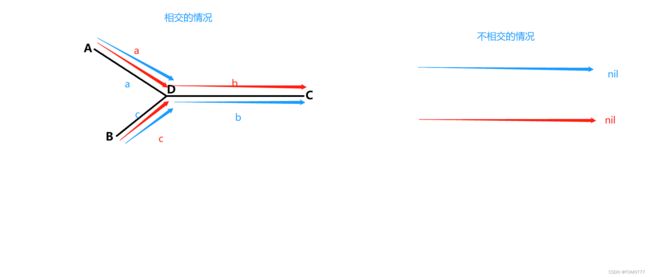
相交的情况：
headA从A出发，一直往后面走到C，走到C之后，headA从B出发，然后走到D。
headB从B出发，一直往后走到C，走到C之后，headB从A出发，然后走到D。
这个过程我们可以发现走过的路径长度相同都是a+b+c，而且两个指针都是每次往后走一步，这就会导致最终必然在D相遇，这里建议在脑中想想这个过程。此时相遇的这个D点就是这个题要找的结果。
不相交的情况：
和上面的过程一样，最终确实是指向一个地方，都指向nil。自己想想确实是这样。

func getIntersectionNode(headA, headB *ListNode) *ListNode {
    cur1:=headA
    cur2:=headB
    for cur1!=cur2{
        if cur1==nil{
            cur1=headB
        }else{
            cur1=cur1.Next
        }

        if cur2==nil{
            cur2=headA
        }else{
            cur2=cur2.Next
        }
    }

    return cur1
}

这个思路确实清楚，但是我肯定想不出来。我只能总结一个道理：多观察性质和多总结。
只要以相同的速度前进，就一定有机会见面。
时间复杂度o(n),空间o(1)

环形链表

我拿到这个题目前我其实做过类似的。所以判断环的思路我是这么想到，用的双指针。fast和slow，fast一次走两步，slow一次走一步，如果有环就有相遇的可能性，这个和跑步套圈一个道理，这里我再做进一步的解释，有人可能有这种想法，我知道会相遇，当时如果在刚好相遇那里我跨了一步，又错开了咋办呢，这种想法是错的，这个过程是可以描述的，这里我用相对运动来解释，感觉就显得简单易懂：快的速度是2，慢的速度是1，那么快的去追慢的，此时快指针的相对速度就是1，那么这种种追法就是一步一步的追，不存在什么跨格错位的可能性（我感觉是相当清楚），如果你是快的走三步，慢的走一步，折才可能有这种跨格错位的可能性。如果没环那就可能fast往后走一步或者走两步的地方是空。这就进行返回。

第一次尝试：我问题出在，没读清楚题目
这个版本是错的，我只进行了环的判断，然后就返回这个相遇的结点，题目要求的是返回这个环的起点。所以要再改改。

双指针写法

然而我真正再改的过程中发现难得根本不在判断环，而是在找到这个起点。在这里我又卡住了。
所以这里我又去学了怎么找这个入口：

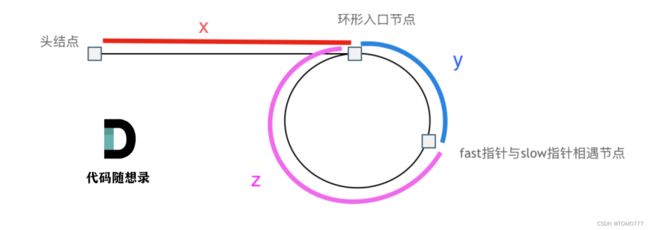
这个我感觉我第一次想的时候，我是真想不到，看了有些题解，只告诉你，反正到slow从头结点走，然后fast从相遇的位置开始走，最后两个指针相遇了这个结点就是入口，这个结论我当时看到，脑子里就是一头雾水，为什么要这么做？
这是有公式推导的，我感觉这个过程就当积累下来了。我按我个人的理解写一下这个推导：
slow去指向头结点，fast去指向相遇的结点，为啥要这么做？这其实是这个过程的运动过程中存在的等式关系,
都从头结点开始，slow一次一步，fast一次两步，最终相遇在某点，此时可得出一些结论，慢指针走到相遇点的路径：x+y,快指针走到相遇点的路径：x+y+n(y+z)。此时再由fast一次两步，slow一次一步，所以路径长度之间有二倍的关系，即2(x+y)=x+y+n(y+z)，这里两边移项进一步化简：得到x=(n-1)(y+z)+z这样的结论，这样可以更加清楚的理解过程，slow走x到入口，等于fast从相遇点走z+(n-1)圈，刚好在入口处相遇。所以此时可以推出这样的结论：
slow从头结点出发，fast从相遇点出发，最终两个点相遇时，这个点就是入口。针对这个结论就可以写一个函数之间求出出口了。

综上：这个题就只有两个步骤：1.判断有没有环。2.找入口。

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */


func detectCycle(head *ListNode) *ListNode {
    if head==nil||head.Next==nil{
        return nil
    }
    fast,slow:=head,head
    var judge bool = false
    for fast.Next!=nil&&fast.Next.Next!=nil{
        fast=fast.Next.Next
        slow=slow.Next
        if fast==slow{
            judge = true
            break
        }
    }

    if judge == true{
        slow = head
        for slow!=fast{
            slow=slow.Next
            fast=fast.Next
        }
        return slow
    }

    return nil
}

这个就是我写对了的版本。

---

总结：
今天的题目我感觉就比昨天的难很多了，有很多的数学推导。所以做题有时候起手没什么感觉，就要从数学推导这方面去思考，这就是思路。