数据结构二叉树详解(C语言)
二叉树详解
- 二叉树的概念
-
- 大堆和小堆
- 堆的插入和删除
- 堆排序
- 堆的Topk查找
- 二叉树遍历
- 二叉树常见问题
- 二叉树的创建和销毁
- 力扣在线oj常见笔试题
二叉树的概念
树是什么:
在数据结构中,树是一种数据的存储结构,他的结构像是一个颗倒着的树,一个数只能有一个根,一个根可以有很多树干,从树干往上可以有很多根树杈,树杈上面又可以长出很多树枝,树枝上面可以有很多树叶。每个树都有根,每个树杈都是从树干上长出来的,每个树枝又都是从树杈上长出来的,每个树叶都是从树枝上长出来的。
我们来用一张图解释一下树:
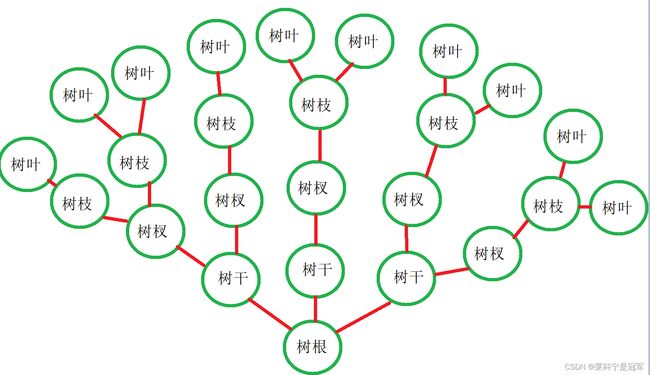
每颗树都只有一个树根,但是可以有很多个树干,树干和树干之间是互不相关的,如果去掉树根,每个树干都可以看做是一颗单独的树,把树干去掉,每颗树杈也可以看做是单独的树,如果一个颗树从树根往上被砍掉,也就是这颗树只有树根,那么这就是一颗空树。
把上图的树倒过来就是数据结构里的树:

树和非树的区别:
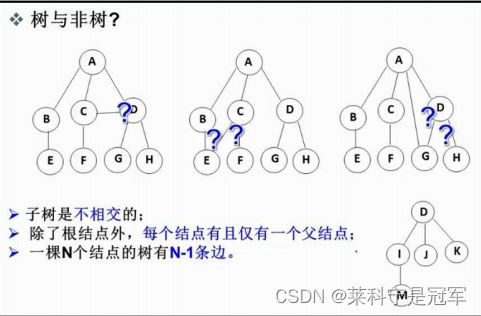
树的相关概念:
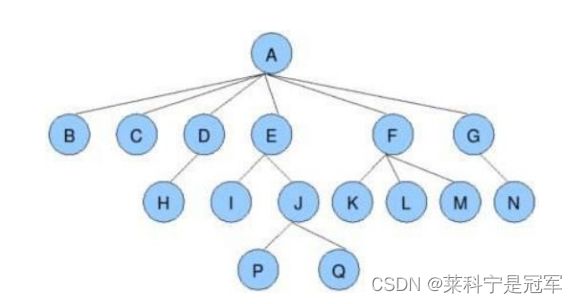
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
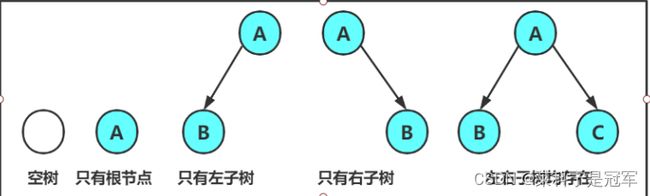
二叉树:
从根节点开始,每个节点的子节点不能超过2
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
-
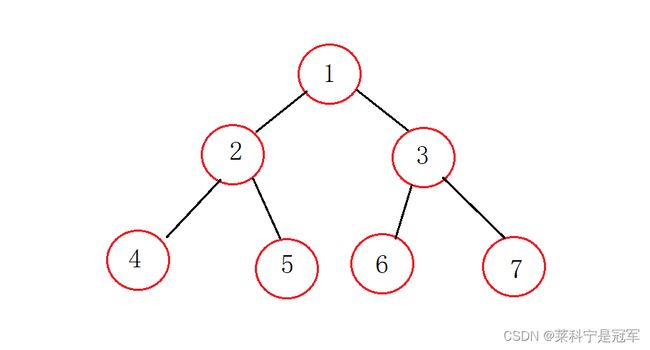
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
-
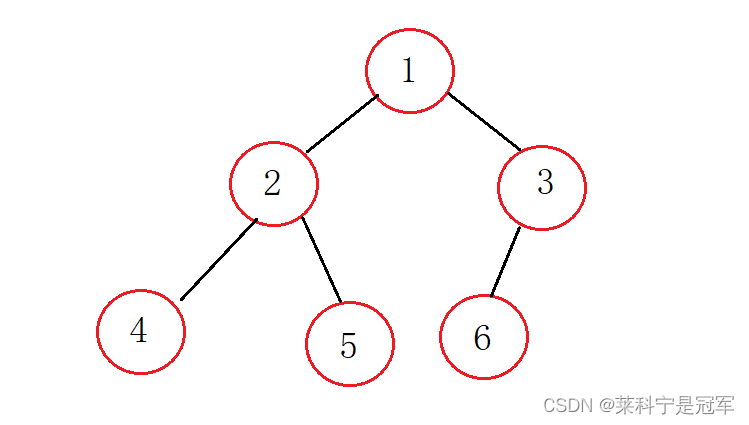
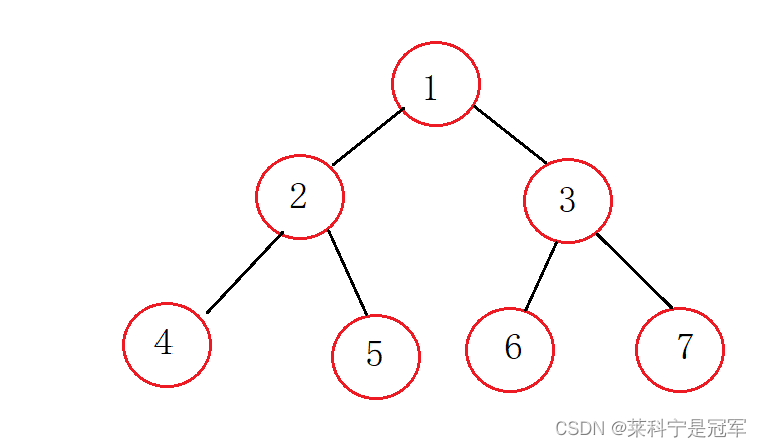
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
大堆和小堆
我们用二叉树来理解一下大堆和小堆:
大堆:所有的父节点都要大于子节点,所有的子节点都要小于父节点,堆顶的数据,也就是根部是最大的
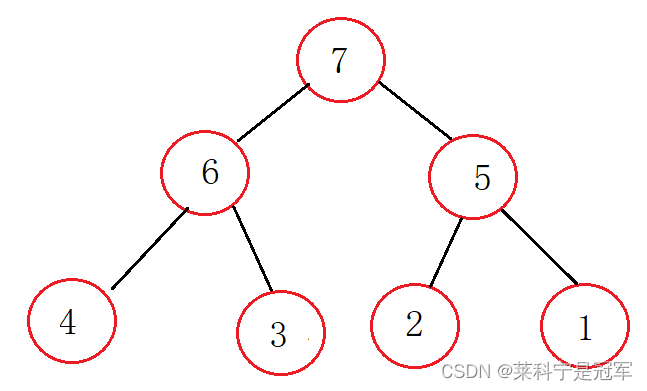
小堆:所有的父节点都要小于子节点,所有的子节点都要大于父节点,堆顶的数据是最小的
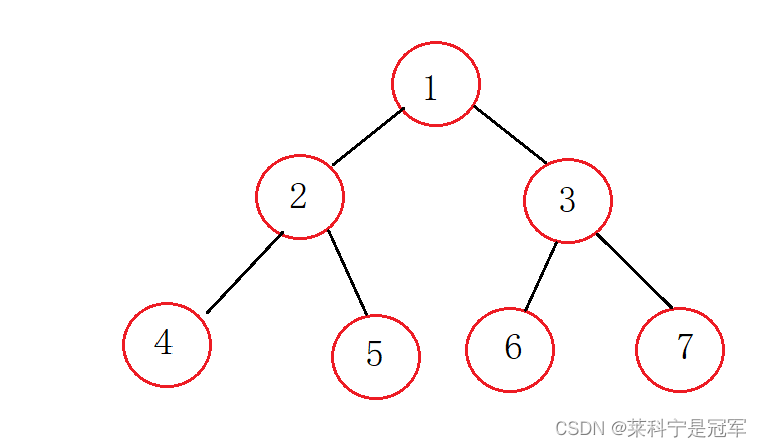
堆总是完全二叉树
通过上面的介绍,我们大致了解了二叉树以及大堆和小堆的概念,那么堆在数据结构中是如何实现的呢?
首先我们用最简单的方式来实现堆 ------ 数组
他的逻辑结构如上图所示,总共有7个接地那,那他的物理结构要放在数组里,就要开辟一个7个int类型的数组。
那是如何放进数组中的:

我们把上面的堆分成3层,每一层的数据按照从左到右,从上到下存入数组中。
再通过一张图片俩分析:

堆的插入和删除
我们来用动态数组实现一下堆的插入和删除:
首先定义一个结构体:
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;//元素个数
int capacity;//动态内存大小
}Heap;
初始化:
//初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->a = NULL;
hp->capacity = 0;
hp->size = 0;
}
插入:
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
//断言
assert(hp);
//当元素个数等于数组大小时
if (hp->capacity == hp->size)
{
//将数组大小扩容至之前的两倍
//如果是初次扩容,开辟4个空间
int newnode = hp->capacity == 0 ? 4 : hp->capacity * 2;
int* p = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newnode);
if (p == NULL)
{
perror("malloc");
exit(-1);
}
hp->a = p;
hp->capacity = newnode;
}
//找到堆的底部插入
hp->a[hp->size++] = x;
判断是否需要向上调整,大堆
AdjustUpMax(hp->a,hp->size - 1,hp->size);
//判断是否需要向上调整,小堆
//AdjustUpMin(hp->a, hp->size - 1, hp->size);
}
这里重点是向上调整部分:AdjustUpMin(向上调整为小堆)
AdjustUpMax(向上调整为大堆)
我们来仔细剖析向上调整:
假设现在有一个空堆,我们要创建一个小堆:
在首次插入元素的时候,用size作为下标,也就是0,那么在插入第二个元素时,下标是1,等于是先插入左子树,然后size再次加1等于2,再插入元素,等于是插入右子树,以此类推,堆是一个完全二叉树,所以不会存在左子树为空,右子树不为空的情况

这个时候数组下标为0的位置就是堆顶,在插入数据后将size++
,记录数组里的元素个数,并且作为下一次插入的下标。
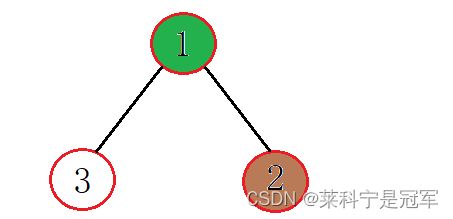
再插入一个2:

2比3要小,也就是子树比父树要大,这时候交换位置:
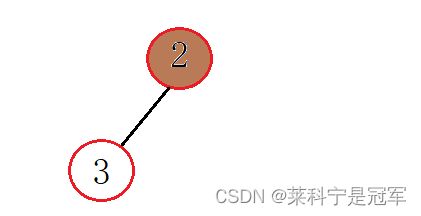
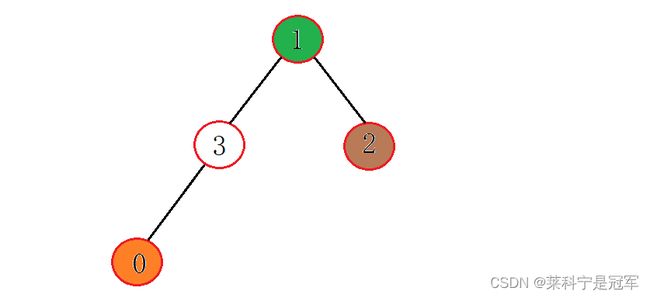
然后再插入一个1:
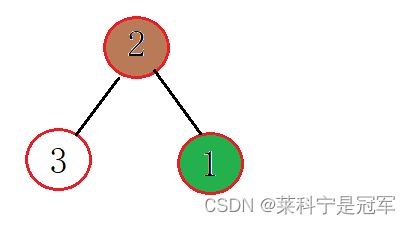
调整过后,再次和父节点比较,0比1小,再次调整:
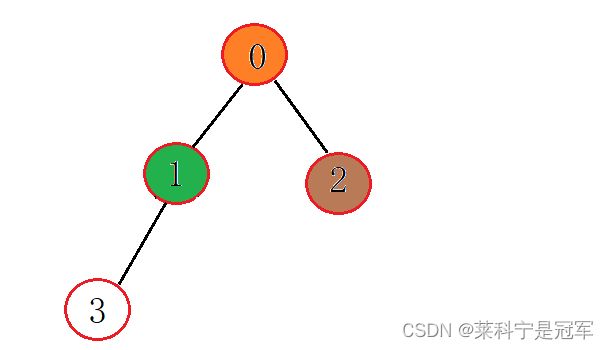
直到调整至下标为0的位置,结束向上调整,这个时候最小的数已经被调整到堆顶,形成小堆
代码实现:
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//判断是否需要交换,像上调整,调整为小堆
void AdjustUpMin(HPDataType* a, int child, int n)
{
//child作为插入元素的下标
//找到child的父节点
int parent = (child - 1) / 2;
//当子节点来到堆顶的位置,就不需要再向上调整了
while (child > 0)
{
//如果子树比父数小
if (a[child] < a[parent])
{
//交换
Swap(&a[child],&a[parent]);
//向上调整,让子节点等于父节点,成为新的子节点
child = parent;
//在利用上面的公式求出父节点的下标
parent = (child - 1) / 2;
}
//如果插入的数不小于父节点,则不需要调整,直接挑出循环
else
{
break;
}
}
}
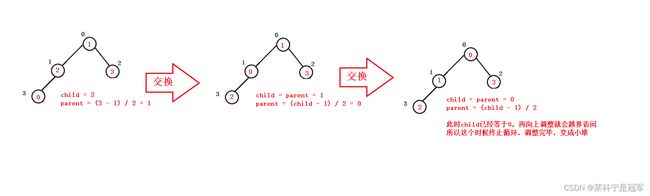
向上调整大堆:
和调整小堆的原理是一样的,但是是调整的条件判断要改成:
当子节点大于父节点的时候才发生交换:
//判断是否需要交换,像上调整,调整为大堆
void AdjustUpMax(HPDataType* a, int child, int n)
{
assert(a);
//找到父节点的下标
int parent = (child - 1) / 2;
while (child > 0)
{
//如果孩子小于父亲
if (a[child] > a[parent])
{
//交换
Swap(&a[child],&a[parent]);
//向上调整
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
堆的删除:
堆的删除是删除堆顶的数据,假设现在有一个小堆,堆顶的元素就是最小的,如果删除了堆顶的元素,那么让谁来做堆顶?
来分析一下:
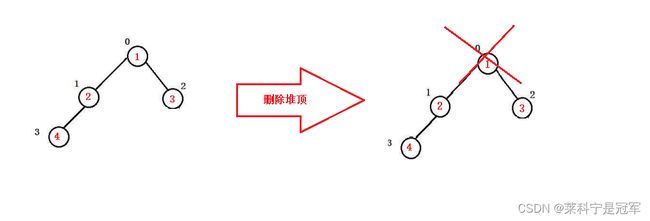
小堆的堆顶一定是最小的那个,所要在删除1以后,就要从1的左树和右树当中选出一个较小值来作为新的堆顶,1的左树是2,右树是3,所以要用2来做新的堆顶。
那怎样删除堆顶的元素呢?我们换一种思路,向下调整:
1,先将堆顶的数据和堆顶的数据交换
2,将数组的长度减1,达到删除的效果
3,将堆顶的新数据向下调整

向下调整:
1,从0开始,找到子树和右树较小的那个
2,交换
3,向下调整,找到新的父节点,继续调整

代码实现:
//判断是否需要交换,像下调整小堆
void AdjustDownMin(HPDataType* a, int parent, int n)
{
assert(a);
//找到左子树
int child = parent * 2 + 1;
//当子树大于数组长度循环停止
while (child < n)
{
//child + 1 得到右树,对比找较小值
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
//子树小于父数,交换
if (a[child] < a[parent])
{
Swap(&a[child],&a[parent]);
parent = child;
child = child * 2 + 1;
}
//父数小于子树,跳出循环
else
{
break;
}
}
}
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
if (hp->size == 0)
{
printf("堆为空\n");
return;
}
//将堆顶数据和堆底数据交换,size--
Swap(&hp->a[0],&hp->a[hp->size - 1]);
hp->size--;
再将堆顶的数据向下调整,大堆
//AdjustDownMax(hp->a,0,hp->size);
//再将堆顶的数据向下调整,小堆
AdjustDownMin(hp->a, 0, hp->size);
}
大堆向下调整:
和小堆的原理一样,只需要在判断是否需要交换时修改条件,子节点大于父节点才交换
//判断是否需要交换,像下调整大堆
void AdjustDownMax(HPDataType* a, int parent, int n)
{
assert(a);
//找到左子树
int child = parent * 2 + 1;
//找到右子树
/*int child = (parent + 1) * 2;*/
while (child < n)
{
//找出左子树和右子树大的那个节点
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
/*if (child < n && a[child] < a[child - 1])
{
child--;
}*/
if (a[parent] < a[child])
{
Swap(&a[parent],&a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//找出左子树和右子树大的那个节点
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
为什么在找较小值要加上 child + 1 < n 这个条件呢?
假设,堆的最后一个数据是左子树,如果加一就超过了数组长度,所以child + 1必须小于数组的长度
堆排序
假设现在有一个数组,数组中有10个元素,
【1,2,3,4,5,6,7,8,9,10】
如何将这组数据变成大堆
首先来分析一下思路,将这个数组转换成堆,逻辑层面是这样的:
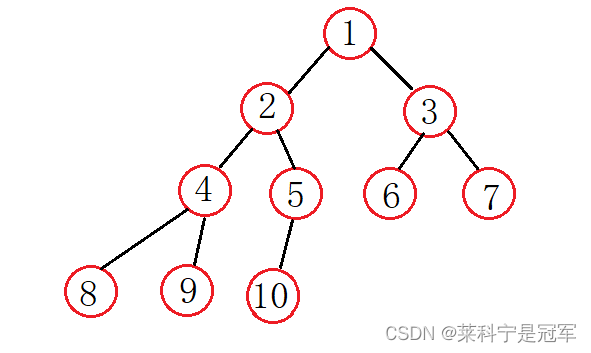
怎样才能让这颗数有序:
1,暴力解法
可以通过上面的HeapPush函数来排序,新建一个堆,将数组的元素依次插入堆,让HeapPush函数取向上调整,然后将堆拷贝到数组,达到排序的效果:
// 对数组进行堆排序,大堆
void HeapSortMax(int* a, int n)
{
//暴力解法
//新建一个堆,将数组的元素依次插入
//使用HeapPush自动排序
Heap hp;
HeapInit(&hp);
int i = 0;
for (i = 0; i < n; i++)
{
HeapPush(&hp,a[i]);
}
//将堆拷贝至原来的数组
memcpy(a,hp.a,sizeof(a[0]) * n);
}
2,排序算法:
1,向上调整法:
我们用一个树来做演示:
(排成小堆)

核心思想是,从下标为1的位置开始向上调整,然后把每个下标的位置都向上调整一遍,达到排序的效果
代码实现:
// 对数组进行堆排序,小堆
void HeapSortMin(int* a, int n)
{
int i = 0;
//从下标为1的位置开始,依次向上调整
for (int i = 1; i < n; i++)
{
//用i作为下标,向上调整
AdjustUpMin(a, i,n);
}
}
排成大堆:
只需将AdjustUpMin换成AdjustUpMax即可
// 对数组进行堆排序,大堆
void HeapSortMin(int* a, int n)
{
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//建大堆,向下调整
AdjustDownMin(a, i, n);
}
}
向下调整法:
核心思想:
从堆的最后一个数据的父节点开始向下调整,也就是堆的倒数第二层,然后依次排序,直到排序到堆顶,排序结束
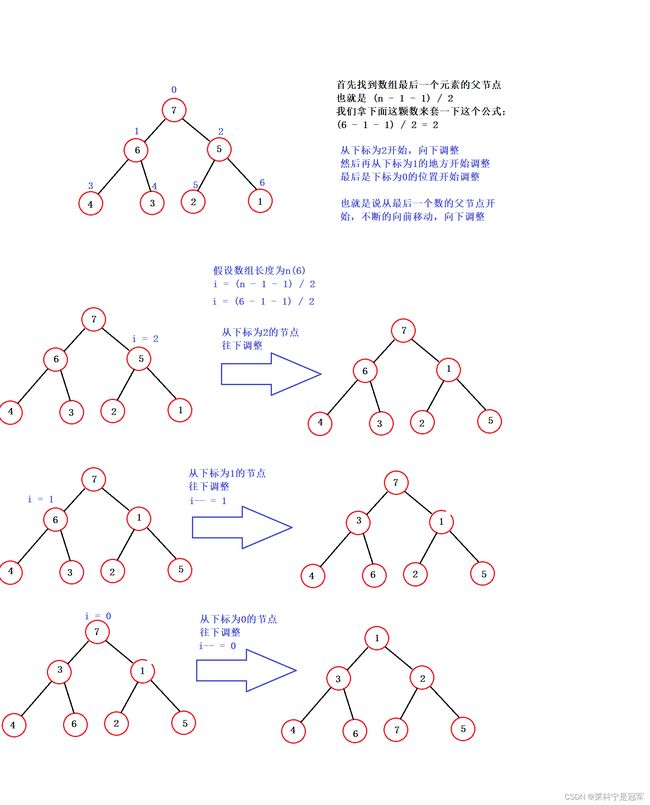
从上面的向上调整和向下调整两种方法的图片来看,向下调整的时间复杂度明显要优于向上调整
代码实现:
// 对数组进行堆排序,小堆
void HeapSortMin(int* a, int n)
{
int i = 0;
//找到数组最后一个数据的父节点
//当父节点小于0时,排序完成
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//建大堆,向下调整
//AdjustDownMax(a, i, n);
//建小堆,向下调整
AdjustDownMin(a,i,n);
}
}
将堆排成升序或者降序:

从上图看到,两个堆一个是小堆,一个是大堆,但是将他们放入数组中排列是时不规则的,将堆排成升序和降序的意思就是,将一个堆放入数组展示,能展现出升序和降序
思路:
如果要排序成升序,首先要让堆成为大堆,这样堆顶的元素就是最大的,然后将堆顶的元素和堆底最后一个元素交换,这样最大的元素就到了最末尾,然后依次向前推,交换堆顶的元素,向下排序,最后就会成为升序
如果要排序成降序,首先要让堆成为小堆,这样堆顶的元素就是最小的,然后将堆顶的元素和堆底的最后一个元素交换,这样最小的元素就到了最末尾,然后依次向前推,交换堆顶的元素,向下排序,最后就会成为降序
假设我们要将左边的小堆排成升序:
1,让其变成大堆,让最大的数到堆顶
2,用一个变量控制下标,从堆底最后一个数据开始向前
,依次和堆顶的数据交换,向下排序
3,当将整个堆的元素都和堆顶的元素交换,向下排序一次,就会成为升序
上图:

代码实现:
//堆排序
void HeapSort(Heap* hp)
{
//先排成大堆
int i = 0;
for (i = 1; i < hp->size; i++)
{
AdjustUpMax(hp->a,i,hp->size);
}
printf("排成大堆:");
HeapPrint(hp);
//排升序
int end = hp->size - 1;
int y = 0;
while (end > 0)
{
//将顶部和底部交换
Swap(&hp->a[0], &hp->a[end]);
//堆顶最大的数被换到末尾,end--,末尾最大的数不参与排序
end--;
//向下排序,选出最大的放在堆顶
AdjustDownMax(hp->a, 0, end);
printf("第%d次排序:",++y);
HeapPrint(hp);
}
}
同理,如果是要排成降序,首先要排成小堆,然后去堆顶最小的数替换到堆末尾,在使用end作为下标,依次向前推进,不断的将次小的数替换下来,最终成为降序
降序代码实现:
//堆排序
void HeapSort(Heap* hp)
{
先排成小堆
int i = 0;
for (i = (hp->size - 1 - 1) / 2; i >= 0; i--)
{
AdjustDownMin(hp->a,i,hp->size);
}
//排降序
int end = hp->size - 1;
while (end > 0)
{
//将顶部和底部交换,最小的数被换到末尾
Swap(&hp->a[0],&hp->a[end]);
//向下排序,再找最小的数
AdjustDownMin(hp->a,0,end);
end--;
}
}
堆的Topk查找
Topk问题:
在一组数据中找出最大的K个数,排成小堆或这找出最小的K个数,排成大堆。
也就是说将最大或者最小的K个数找出来,排成大堆或者小堆
思路:
假设要找出,最大的K个数,排成小堆:
1,先将数组中任意K个数放入堆中
2,将堆排成小堆
3,遍历数组,用数组中的每一个元素和堆顶的数据比较,当数组中的数据比堆顶数据要大时,替换,然后向下排序
4,遍历完数组,最大的K个数已经到了堆中
原理:将任意K个数排成小堆,这样堆顶的数据就是最小的,如果这个时候有比堆顶大的数据,就替换下来,然后再向下调整,这样堆底的数据永远都是堆中最小的。
代码实现:
// 找最大的前K个,建立K个数的小堆
void MaxTopKMin(Heap* hp,int* a, int n, int k)
{
//先将数组的任意前k个数放入堆
HeapInit(hp);
hp->a = (int*)realloc(hp->a,sizeof(int) * k);
hp->capacity = k;
hp->size = k;
memcpy(hp->a,a,sizeof(int) * k);
//让堆变成小堆
int i = 0;
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDownMin(hp->a,i,k);
}
//遍历数组,遇到比堆底大的数据就替换下来
//然后向下排序
i = 0;
while (i < n)
{
//替换
if (a[i] > hp->a[0])
{
hp->a[0] = a[i];
//向下排序
AdjustDownMin(hp->a, 0, k);
}
i++;
}
}
同理,找出最小的K个数,排成大堆
1,将任意K个数放入堆中
2,排成大堆
3,只要比堆顶的数小,就替换
4,向下排序,保证堆顶的数据是堆中最大的
代码实现:
// 找最小的前K个,建立K个数的大堆
void MinTopkMax(Heap* hp, int* a, int n, int k)
{
HeapInit(hp);
hp->capacity = k;
hp->size = k;
hp->a = (int*)realloc(hp->a,sizeof(int) * k);
memcpy(hp->a,a,sizeof(int) * k);
//让堆成为大堆
int i = 0;
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
//调整
AdjustDownMax(hp->a,i,k);
}
//此时堆顶的数据是最大的
HeapPrint(hp);
i = 0;
while (i < n)
{
//只要比堆顶的数据小,替换,然后向下排序
if (a[i] < hp->a[0])
{
hp->a[0] = a[i];
//向下调整
AdjustDownMax(hp->a,0,k);
}
i++;
}
}
堆问题的全部代码:
Heap.h
#define _CRT_SECURE_NO_WARNINGS
#includeHeap.c
#define _CRT_SECURE_NO_WARNINGS
#include"Heap.h"
//初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->a = NULL;
hp->capacity = 0;
hp->size = 0;
}
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
//方法1,将数组的元素依次使用HeapPush插入到堆
/*int i = 0;
for (i = 0; i < n; i++)
{
HeapPush(hp,a[i]);
}*/
//方法2,建堆算法
//1,向下调整
//先找到堆的最后一个数据,然后找到他的父节点
//依次向下调整
int i = 0;
//for (i = (n - 1 - 1) / 2; i >= 0; i--)
//{
// //分成成数个小数,向下调整
// //AdjustDownMax(a,i,n);//大堆
// AdjustDownMin(a,i,n);//小堆
//}
//2,向上调整
//假设下标为0的堆顶数据是有序,从下标为1的位置开始
//依次向上调整
for (i = 1; i < n; i++)
{
//向上调整,大堆
//AdjustUpMax(a,i,n);
//向上调整,小堆
AdjustUpMin(a,i,n);
}
hp->a = (int*)realloc(hp->a,sizeof(int) * n);
hp->capacity = n;
hp->size = n;
memcpy(hp->a,a,sizeof(int) * n);
}
//打印堆
void HeapPrint(Heap* hp)
{
if (hp->size == 0)
{
printf("堆为空\n");
return;
}
int i = 0;
for (i = 0; i < hp->size; i++)
{
printf("%d ",hp->a[i]);
}
printf("\n");
}
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//判断是否需要交换,像上调整,调整为大堆
void AdjustUpMax(HPDataType* a, int child, int n)
{
assert(a);
//找到父节点的下标
int parent = (child - 1) / 2;
while (child > 0)
{
//如果孩子小于父亲
if (a[child] > a[parent])
{
//交换
Swap(&a[child],&a[parent]);
//向上调整
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//判断是否需要交换,像上调整,调整为小堆
void AdjustUpMin(HPDataType* a, int child, int n)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
//断言
assert(hp);
//当元素个数等于数组大小时
if (hp->capacity == hp->size)
{
//将数组大小扩容至之前的两倍
//如果是初次扩容,开辟4个空间
int newnode = hp->capacity == 0 ? 4 : hp->capacity * 2;
int* p = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newnode);
if (p == NULL)
{
perror("malloc");
exit(-1);
}
hp->a = p;
hp->capacity = newnode;
}
//找到堆的底部插入
hp->a[hp->size++] = x;
判断是否需要向上调整,大堆
//AdjustUpMax(hp->a,hp->size - 1,hp->size);
//判断是否需要向上调整,小堆
AdjustUpMin(hp->a, hp->size - 1, hp->size);
}
//判断是否需要交换,像下调整大堆
void AdjustDownMax(HPDataType* a, int parent, int n)
{
assert(a);
//找到左子树
int child = parent * 2 + 1;
//找到右子树
/*int child = (parent + 1) * 2;*/
while (child < n)
{
//找出左子树和右子树大的那个节点
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
/*if (child < n && a[child] < a[child - 1])
{
child--;
}*/
if (a[parent] < a[child])
{
Swap(&a[parent],&a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//判断是否需要交换,像下调整小堆
void AdjustDownMin(HPDataType* a, int parent, int n)
{
assert(a);
//找到左子树
int child = parent * 2 + 1;
//当子树大于数组长度循环停止
while (child < n)
{
//child + 1 得到右树,对比找较小值
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
//子树小于父数,交换
if (a[child] < a[parent])
{
Swap(&a[child],&a[parent]);
parent = child;
child = child * 2 + 1;
}
//父数小于子树,跳出循环
else
{
break;
}
}
}
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
if (hp->size == 0)
{
printf("堆为空\n");
return;
}
//将堆顶数据和堆底数据交换,size--
Swap(&hp->a[0],&hp->a[hp->size - 1]);
hp->size--;
再将堆顶的数据向下调整,大堆
//AdjustDownMax(hp->a,0,hp->size);
//再将堆顶的数据向下调整,小堆
AdjustDownMin(hp->a, 0, hp->size);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
if (hp->size == 0)
{
printf("堆为空\n");
}
return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
if (hp->size == 0)
{
printf("堆为空\n");
exit(-1);
}
return hp->size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{
assert(hp);
return hp->size == 0;
}
// 对数组进行堆排序,大堆
void HeapSortMax(int* a, int n)
{
暴力解法
新建一个堆,将数组的元素依次插入
使用HeapPush自动排序
//Heap hp;
//HeapInit(&hp);
//int i = 0;
//for (i = 0; i < n; i++)
//{
// HeapPush(&hp,a[i]);
//}
将堆拷贝至原来的数组
//memcpy(a,hp.a,sizeof(a[0]) * n);
//排序算法
//找到堆底的数据,再找到堆底数据的父节点
int i = 0;
//从下标为1的位置开始,依次向上调整
/*for (int i = 1; i < n; i++)
{
AdjustUpMax(a, i,n);
}*/
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//建大堆,向下调整
AdjustDownMax(a, i, n);
}
}
// 对数组进行堆排序,小堆
void HeapSortMin(int* a, int n)
{
int i = 0;
//从下标为1的位置开始,依次向上调整
/*for (int i = 1; i < n; i++)
{
AdjustUpMin(a, i,n);
}*/
//找到数组最后一个数据的父节点
//当父节点小于0时,排序完成
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//建小堆,向下调整
AdjustDownMin(a, i, n);
}
}
// 找最大的前K个,建立K个数的小堆
void MaxTopKMin(Heap* hp,int* a, int n, int k)
{
//先将数组的任意前k个数放入堆
HeapInit(hp);
hp->a = (int*)realloc(hp->a,sizeof(int) * k);
hp->capacity = k;
hp->size = k;
memcpy(hp->a,a,sizeof(int) * k);
//让堆变成小堆
int i = 0;
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDownMin(hp->a,i,k);
}
//遍历数组,遇到比堆底大的数据就替换下来
//然后向下排序
i = 0;
while (i < n)
{
//替换
if (a[i] > hp->a[0])
{
hp->a[0] = a[i];
//向下排序
AdjustDownMin(hp->a, 0, k);
}
i++;
}
}
// 找最小的前K个,建立K个数的大堆
void MinTopkMax(Heap* hp, int* a, int n, int k)
{
HeapInit(hp);
hp->capacity = k;
hp->size = k;
hp->a = (int*)realloc(hp->a,sizeof(int) * k);
memcpy(hp->a,a,sizeof(int) * k);
//让堆成为大堆
int i = 0;
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
//调整
AdjustDownMax(hp->a,i,k);
}
//此时堆顶的数据是最大的
HeapPrint(hp);
i = 0;
while (i < n)
{
//只要比堆顶的数据小,替换,然后向下排序
if (a[i] < hp->a[0])
{
hp->a[0] = a[i];
//向下调整
AdjustDownMax(hp->a,0,k);
}
i++;
}
}
//堆排序
void HeapSort(Heap* hp)
{
//先排成大堆
int i = 0;
/*for (i = (hp->size - 1 - 1) / 2; i >= 0; i--)
{
AdjustDownMax(hp->a,i,hp->size);
}*/
for (i = 1; i < hp->size; i++)
{
AdjustUpMax(hp->a,i,hp->size);
}
printf("排成大堆:");
HeapPrint(hp);
//排升序
int end = hp->size - 1;
int y = 0;
while (end > 0)
{
//将顶部和底部交换
Swap(&hp->a[0], &hp->a[end]);
//堆顶最大的数被换到末尾,end--,末尾最大的数不参与排序
//向下排序,选出最大的放在堆顶
AdjustDownMax(hp->a, 0, end);
end--;
printf("第%d次排序:",++y);
HeapPrint(hp);
}
先排成小堆
//int i = 0;
//for (i = (hp->size - 1 - 1) / 2; i >= 0; i--)
//{
// AdjustDownMin(hp->a,i,hp->size);
//}
///*for (i = 1; i < hp->size; i++)
//{
// AdjustUpMin(hp->a,i,hp->size);
//}*/
//HeapPrint(hp);
排降序
//int end = hp->size - 1;
//while (end > 0)
//{
// //将顶部和底部交换,最小的数被换到末尾
// Swap(&hp->a[0],&hp->a[end]);
// //向下排序,再找最小的数
// AdjustDownMin(hp->a,0,end);
// end--;
//}
}
二叉树遍历
首先来了解一下二叉树的物理结构:
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;//数据
struct BinaryTreeNode* left;//左子树
struct BinaryTreeNode* right;//右子树
}BTNode;
用一个结构体作为二叉树的根,然后再结构体里定义两个结构体指针来做左子树,和右子树
用结构体存储树和用数组存储树是两种完全不同的结构,当left,right为NULL时,表示下面没有节点。
二叉树的遍历分为4种:
1,前序遍历:根 => 左子树 =>右子树
2,中序遍历:左子树 =>根 =>右子树
3,后序遍历:左子树 =>右子树 =>根
4,层序遍历:将二叉树的物理层面展开,像堆那样存入数组,然后遍历
我们来用4张图来解释上面的遍历方式:
1,前序遍历
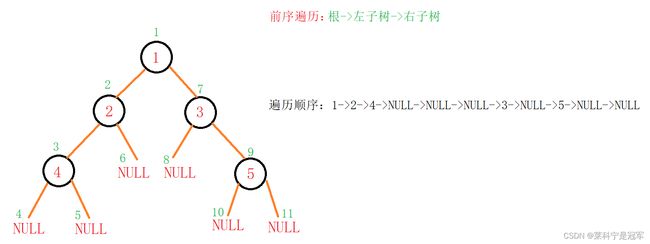
前序遍历的原则是先访问根,再访问左子树,最后是右子树
从图看,1是根,左子树是2,右子树是3,当访问完1后,访问1的左子树2,这个时候,要把2也看做是一颗树,那么2就是根,所以根据前序遍历的原则,访问2。
再往下走,访问2的左子树4,而4又可以看做是一颗树,再次用前序遍历原则,先访问根,也就是4,再访问4的左树,4的左树是NULL,也就是叶子节点,然后访问4的右树,4的右树也是NULL
访问完2的左子树,接下来访问2的右子树,2的右子树是NULL
2已经被访问完了,再访问1的右子树,1的右子树是3,3又可以当做是一颗树,访问3的根,再访问3的左子树,3的左子树是NULL,再访问3的右子树5,5又被当成是一个树,访问5的根,再访问5的左子树NULL,再访问5的右子树NULL.
访问完5的右树,整颗树就已经遍历完毕了
(二叉树遍历不论是前,中后都要保持一个原则,除了叶子节点,其他的节点都要单独当成一颗树,然后再遵循遍历原则去遍历)
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
//当root等于空时,返回
if (root == NULL)
{
printf("NULL->");
return;
}
//打印自身节点
printf("%d->",root->data);
//左子树
BinaryTreePrevOrder(root->left);
//右子树
BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
BinaryTreeInOrder(root->left);
printf("%d->",root->data);
BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL->");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d->",root->data);
}
验证一下:
//创建节点
BTNode* Add(int x)
{
BTNode* p = (BTNode*)malloc(sizeof(BTNode));
if (p == NULL)
{
exit(-1);
}
p->data= x;
p->left = NULL;
p->right = NULL;
return p;
}
void test1()
{
//构建二叉树
BTNode* p1 = Add(1);
BTNode* p2 = Add(2);
BTNode* p3 = Add(3);
BTNode* p4 = Add(4);
BTNode* p5 = Add(5);
p1->left = p2;
p1->right = p3;
p2->left = p4;
p3->right = p5;
//前序遍历
printf("前序遍历:");
BinaryTreePrevOrder(p1);
printf("\n");
//中序遍历
printf("中序遍历:");
BinaryTreeInOrder(p1);
printf("\n");
//后序遍历
printf("后序遍历:");
BinaryTreePostOrder(p1);
printf("\n");
}
int main()
{
test1();
return 0;
}
二叉树层序遍历:
这玩意可有点上头了!!!
常规的递归思路不太好玩这个
我们可以借助队列来实现
思路:
1,创建一个队列,将根先插入队列
2,保存队列头部元素,再将队列头部出队列
3,将实现保存好的队列头部的左右数再入队列
上图:
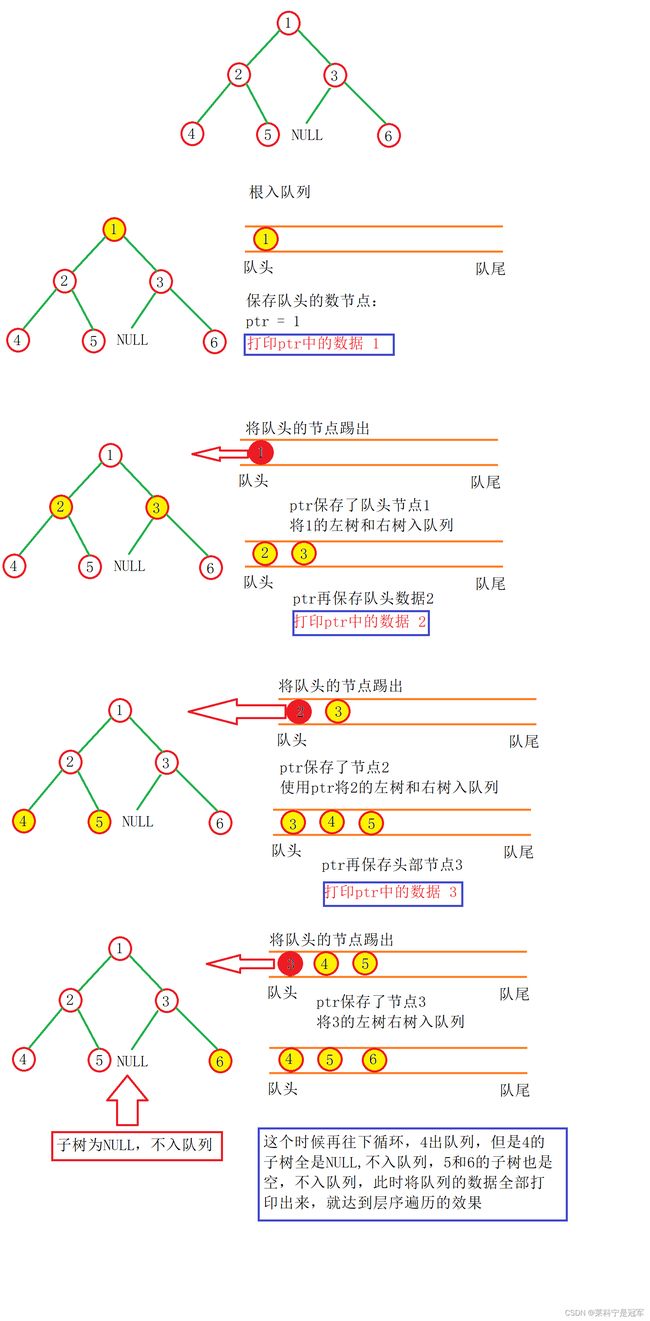
代码实现:
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
//借助队列来实现
//1,先将根入队列
//2,保存队列头部
//3,头部出队列,将左子树和右子树带入
//创建队列并初始化
Queue p;
QueueInit(&p);
//根入队列
QueuePush(&p,root);
//队列不为空继续
while (!QueueEmpty(&p))
{
//保存队头数据
BTNode* ptr = QueueFront(&p);
//打印数据
printf("%d->", ptr->data);
//队头出列
QueuePop(&p);
//子树不为空
//将ptr的左右子树带入队列
if(ptr->left)
QueuePush(&p,ptr->left);
if(ptr->right)
QueuePush(&p,ptr->right);
}
}
队列函数实现:
typedef BTNode* QDataType;
// 链式结构:表示队列
typedef struct QListNode
{
QDataType data;//树
struct QListNode* next;//下一个节点
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* front;//队列头部
QNode* rear;//队列尾部
int size;//记录元素个数
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
//全部初始化为空
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
//申请空间
QNode* p = (QNode*)malloc(sizeof(QNode));
if (p == NULL)
{
perror("malloc");
exit(-1);
}
//将值赋给p
p->data = data;
p->next = NULL;
//第一次入队列
if (q->front == NULL)
{
//第一次入队,两个指针同时指向栈底
q->front = q->rear = p;
}
else
{
//将尾部的next和新节点连接
q->rear->next = p;
q->rear = p;
}
q->size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
//判断是否只有一个节点
if (q->front == q->rear)
{
q->front = NULL;
q->rear = NULL;
}
else
{
//保留头部
QNode* p = q->front;
q->front = q->front->next;
//释放头部
free(p);
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
//判断队列是否为空
if (QueueEmpty(q))
{
printf("队列为空\n");
exit(-1);
}
//返回队头指针的数据
return q->front->data;
}
// 检测队列是否为空,如果为空返回true,如果非空返回false
bool QueueEmpty(Queue* q)
{
assert(q);
//这里可以加上数据个数和尾部指针,也可以不加
//保险一定可以都加上
return q->front == NULL && q->rear == NULL;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
while (q->front)
{
//保留上一个节点,再销毁下一个节点
QNode* p = q->front;
q->front = q->front->next;
free(p);
}
q->size = 0;
q->rear = NULL;
}
二叉树常见问题
1,求二叉树节点的个数
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
//当为空的时候返回0
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) +
BinaryTreeSize(root->right) + 1;
}
2,二叉树的高度
//二叉树的高度
int BinaryTreeHight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
//左树高度
int i = BinaryTreeHight(root->left) + 1;
//右树高度
int j = BinaryTreeHight(root->right) + 1;
//返回最高的那个
return i > j ? i : j;
}
3,二叉树的叶子节点个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
//如果为NULL,不能再继续向下找左树和右树
if (root == NULL)
{
return 0;
}
//一个节点的左右子树都为NULL就是叶子节点
if (root->left == NULL && root->right == NULL)
{
return 1;
}
//以根作为分割,将左树和右树的叶子节点加起来
return BinaryTreeLeafSize(root->left) +
BinaryTreeLeafSize(root->right);
}
4,二叉树查找值为X的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
//root无法返回到最初的递归函数处
return root;
}
//创建两个指针变量来接收返回结果
BTNode* p1 = BinaryTreeFind(root->left,x);
BTNode* p2 = BinaryTreeFind(root->right,x);
//这里要加上p1 != NULL 这个条件
//如果不加上,假如p1是NULL,是不能去访问他的内部数据
if (p1 != NULL && (p1->data = x))
{
return p1;
}
if (p2 != NULL && (p2->data = x))
{
return p2;
}
//如果左树和右树都没有找到,返回NULL
return NULL;
}
5,二叉树第K层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
//为空说明不是节点
if (root == NULL)
{
return 0;
}
//如果节点不为NULL,并且k = 1,说明走到k层
//这个时候返回1
if (k == 1)
{
return 1;
}
/*注意,这里函数的第二个参数不能用k--,--k,或者在前面提前将K-1
因为从左右子树的K层去找,如果先将k-1,那么第二个函数将会往后
一层*/
//将左右数的K层节点加起来返回
return BinaryTreeLevelKSize(root->left,k - 1) +
BinaryTreeLevelKSize(root->right,k - 1);
}
6,判断是否为完全二叉树
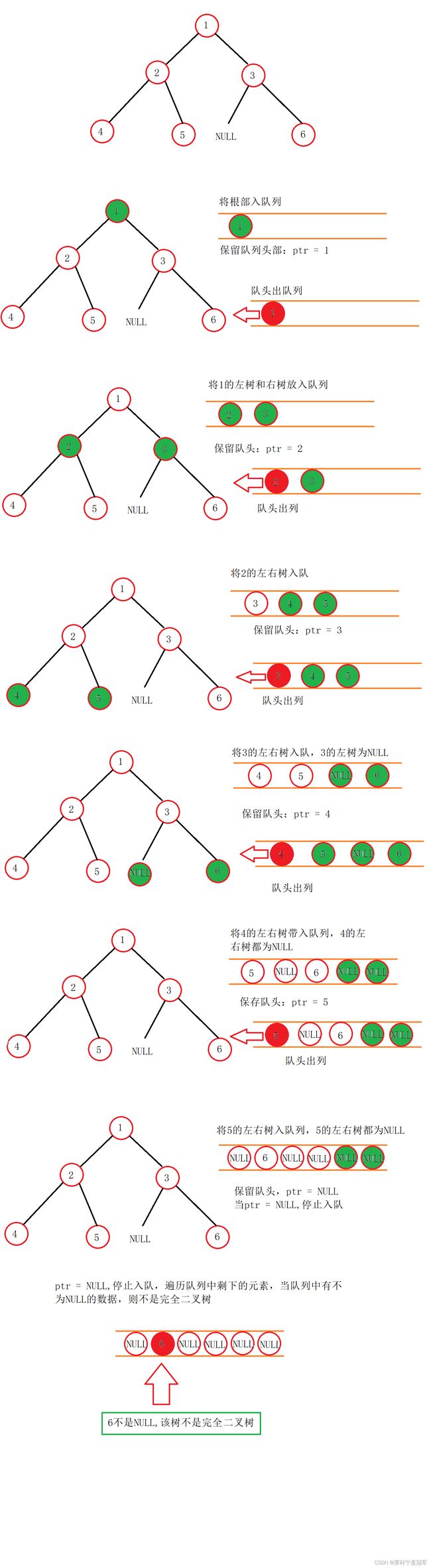
完全二叉树的概念:1.叶子结点只会在最后两层出现, 2.当某个结点左右孩子为空或者右孩子为空时,后面所有结点孩子均为空。
上图:
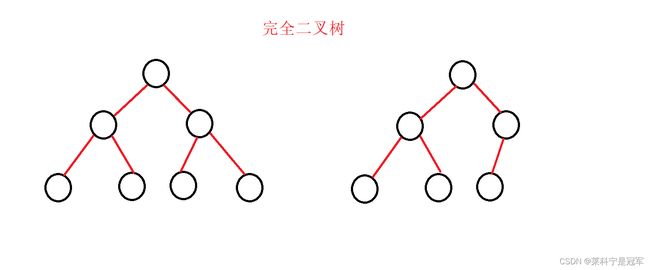
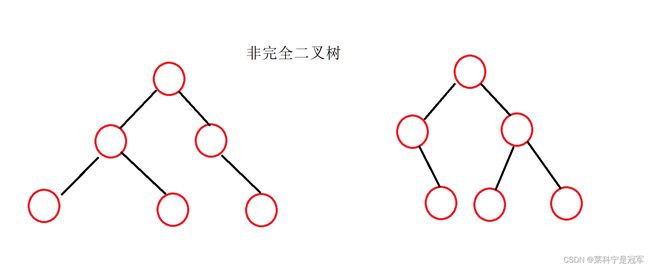
思路:
借助队列,先将根部节点入队,然后保留队列头部节点,将队列头部出队列,将之前保留的节点的左右子树带入队列,依次循环,当遇到第一个为NULL的节点时,不再入队,再遍历队列里剩下的数据,如果有不为NULL的节点,则不是完全二叉树
代码实现:
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
//借用队列来实现
//1,首先根节点入队列
//2,然后pop队列首元素
//3,再将新队头的子树入队列
//4,直到遇到空,停止入队
//5,然后一直pop
//6,如果是完全二叉树,队列最后一个NULL后面不会有其他数据
Queue p;
QueueInit(&p);
QueuePush(&p, root);
//队列为空停止
while (!QueueEmpty(&p))
{
//保存队头
BTNode* ptr = QueueFront(&p);
//队头出列
QueuePop(&p);
//当遇到第一个NULL时,停止循环
if (ptr == NULL)
{
break;
}
//将之前出队的队头的左树和右树入队列
QueuePush(&p,ptr->left);
QueuePush(&p,ptr->right);
}
while (!QueueEmpty(&p))
{
//队列有一个不为空不是完全二叉树
//保存队头
BTNode* ptr = QueueFront(&p);
if (ptr != NULL)
{
//销毁队列
QueueDestroy(&p);
return false;
}
//队头出列
QueuePop(&p);
}
//销毁队列
QueueDestroy(&p);
return true;
}
二叉树的创建和销毁
1,二叉树的创建
假设现有一个数组 int arr[] = {1,2,4,0,0,5,0,7,0,0,3,8,0,0,9,0,0};
(0代表NULL)
用数组里的元素创建一个二叉树:
思路:
通过前序遍历数组,依次创建节点,组成一个二叉树
创建好的二叉树逻辑图:
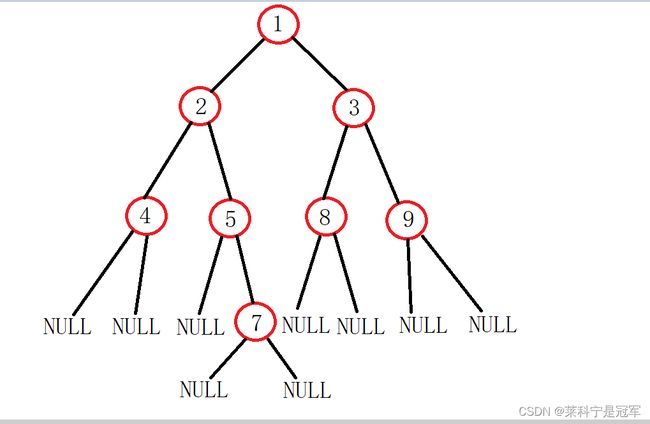
通过前序遍历,递归实现
//二叉树创建
//数组 //数组长度
BTNode* BinaryTreeCreate(int* arr, int* i)
{
//等于0,表示NULL
if (arr[*i] == 0)
{
//这里的i++必须放在括号内,不能放在判断语句中(arr[*i++] == 0)
//不然每次判断都会让i往后走
//只有等于0时,才往后跳过
(*i)++;
return NULL;
}
//创建节点
BTNode* p = (BTNode*)malloc(sizeof(BTNode));
//赋值
p->data = arr[(*i)++];//i++,让数组往后走,达到前序遍历的效果
//递归左子树
p->left = BinaryTreeCreate(arr, i);
//递归右子树
p->right = BinaryTreeCreate(arr, i);
//返回其实节点
return p;
}
2,二叉树的销毁
使用后序遍历是最优的方式:
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
//后序遍历
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
//走完左树,走完右树,再销毁节点
free(root);
root = NULL;
}
力扣在线oj常见笔试题
单值二叉树
代码实现:
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
{
return true;
}
//如果左子树不为NULL,并且和自身节点的值相等
if(root->left != NULL && root->left->val != root->val)
return false;
//如果右子树不为NULL,并且和自身节点的值相等
if(root->right != NULL && root->right->val != root->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
二叉树的最大深度
代码实现:
int maxDepth(struct TreeNode* root){
if(root == NULL)
{
return NULL;
}
//记录左树高度
int i = maxDepth(root->left) + 1;
//记录右树高度
int j = maxDepth(root->right) + 1;
//返回最高的那颗数的深度
return i > j ? i : j;
}
相同的树
代码实现:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//两个都是NULL,相同
if(p == NULL && q == NULL)
return true;
//当上面的if判断没有进去,如果有一个为NULL,肯定不相等
if(p == NULL || q == NULL)
return false;
//都不为NULL,再进行对比
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
二叉树的前序遍历
代码实现:
//计算二叉树节点个数
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
{
return 0;
}
return TreeSize(root->left)
+ TreeSize(root->right) + 1;
}
//将二叉树的节点数据放入数组
void AddTree(struct TreeNode* root,int* arr,int* i)
{
if(root == NULL)
return;
arr[(*i)++] = root->val;
AddTree(root->left,arr,i);
AddTree(root->right,arr,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
//求出树的节点个数
int i = TreeSize(root);
//开辟动态内存
int* arr = (int*)malloc(sizeof(int) * i);
*returnSize = i;
int j = 0;
//将树的节点放入数组
AddTree(root,arr,&j);
//返回数组
return arr;
}
翻转二叉树
代码实现:
struct TreeNode* invertTree(struct TreeNode* root){
if(root == NULL)
return NULL;
//交换左右子树
struct TreeNode* p = root->left;
root->left = root->right;
root->right = p;
invertTree(root->left);
invertTree(root->right);
//返回根节点
return root;
}
对称二叉树
代码实现:
方法1:
struct TreeNode* invertTree(struct TreeNode* root){
if(root == NULL)
return NULL;
//交换左右子树
struct TreeNode* p = root->left;
root->left = root->right;
root->right = p;
invertTree(root->left);
invertTree(root->right);
//返回根节点
return root;
}
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//两个都是NULL,相同
if(p == NULL && q == NULL)
return true;
//当上面的if判断没有进去,如果有一个为NULL,肯定不相等
if(p == NULL || q == NULL)
return false;
//都不为NULL,再进行对比
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
bool isSymmetric(struct TreeNode* root){
//先将root的一颗子树翻转
struct TreeNode*p = invertTree(root->left);
//再用左树和右树对比
bool i = isSameTree(p,root->right);
return i;
}
方法2:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
//两个都是NULL,相同
if(p == NULL && q == NULL)
return true;
//当上面的if判断没有进去,如果有一个为NULL,肯定不相等
if(p == NULL || q == NULL)
return false;
//都不为NULL,再进行对比
if(p->val != q->val)
return false;
//用p的左树对比q的右树
//用p的右树,对比q的左树
//达到对称对比效果
return isSameTree(p->left,q->right) && isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root){
//直接对比左右子树
return isSameTree(root->left,root->right);
}
另一颗树的子树
代码实现:
//比较
bool _test(struct TreeNode* p1,struct TreeNode* p2)
{
if(p1 == NULL && p2 == NULL)
return true;
if(p1 == NULL || p2 == NULL)
return false;
if(p1->val != p2->val)
return false;
return _test(p1->left,p2->left) && _test(p1->right,p2->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//如果两个都为NULL,就是一样的
if(root == NULL && subRoot == NULL)
return true;
//如果有一个为NULL,一个不为NULL,肯定不相等
if(root == NULL || subRoot == NULL)
return false;
//两个都不为NULL,进行比较
if(_test(root,subRoot))
return true;
//左树和右树,有一个相等返回true
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}